轉動運動

rotational motion ppt

2. 轉動運動公式：

Formula for rotation:

\[ 角速率:\omega=\frac{d\theta}{dt}\] \[ 角加速率:\alpha=\frac{d\omega}{dt}\] \[ 等角速率運動:\theta=\theta_0+\omega t \] \[ 等加角速率運動:\] \[ \omega=\omega_0+\alpha t\] \[ \theta=\theta_0+\omega t + \frac{1}{2}\alpha t^2\] \[ \omega^2=\omega_0^2+2\alpha (\theta-theta_0) \]

3. 等角速率運動之模擬：

\[ 等角速率運動:\theta=\theta_0+\omega t \]

from visual import *
R=0.5; x=0.
dotv=vector(0,0.4,0.3)
scene = display(width=800, height=800, center=(5,0,0), background=(0.5,0.5,0))
xaxis=arrow(pos=(0,0,0),axis=(1,0,0),length=3,shaftwidth=0.05,color=color.red)
yaxis=arrow(pos=(0,0,0),axis=(0,1,0),length=3,shaftwidth=0.05,color=color.green)
zaxis=arrow(pos=(0,0,0),axis=(0,0,1),length=3,shaftwidth=0.01,color=color.blue)
floor=box(pos=(5,-R,0),length=10, height=0.1, width=1,color=(0.2,0.2,1))
f = frame()
ball=sphere(frame=f, pos=(0,0,0), radius=R, color=color.red)
dot=sphere(frame=f, pos=dotv, radius=R/5., color=color.yellow)
w=2.*pi/1.
v=R*w
dt=0.01
delta=w*dt
t=0.
while True:
    if(t > 3.): break
    rate(20)
    f.rotate(angle=delta, axis=(0,0,-1), origin=(0,0,0))
    x=x+v*dt
    f.pos=(x,0,0)
    t=t+dt

4. 擺線：

在數學中，擺線（Cycloid）被定義為，一個圓沿一條直線運動時，圓邊界上一定點所形成的軌跡。它是一般旋輪線的一種。

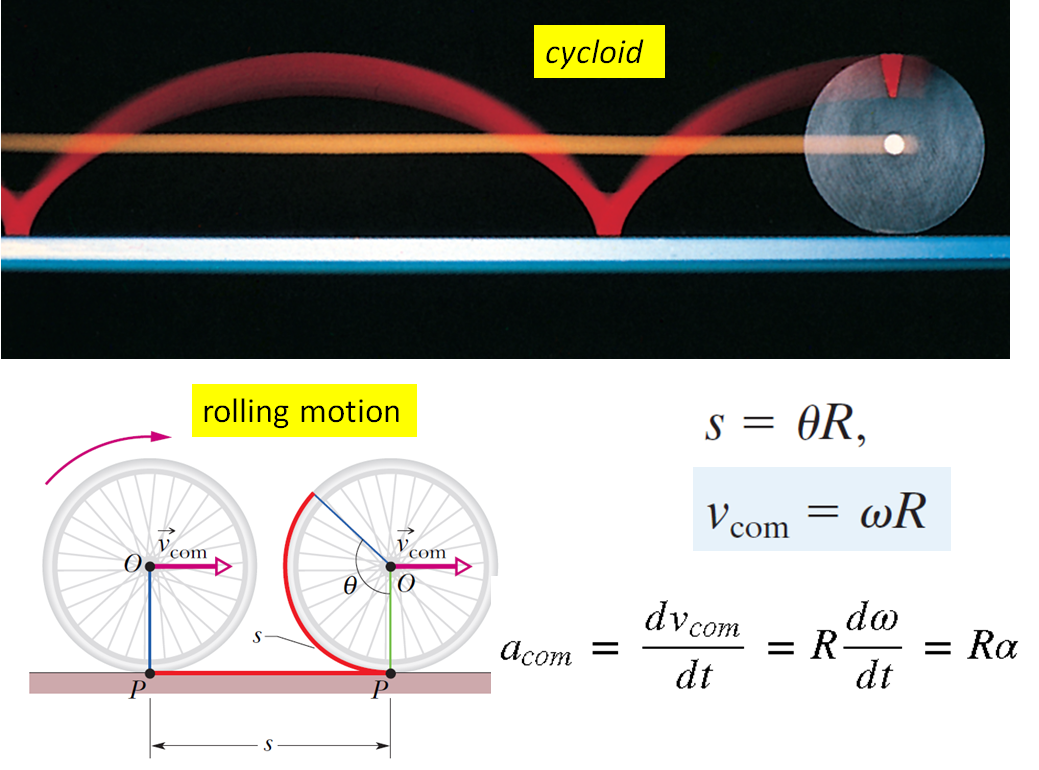
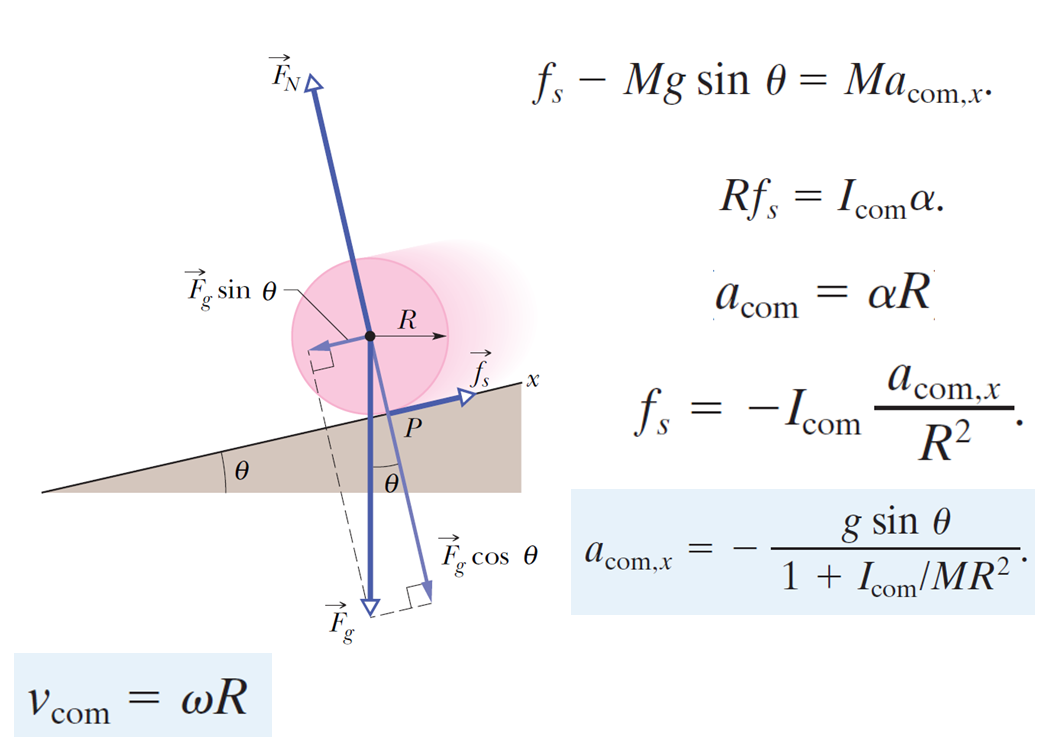
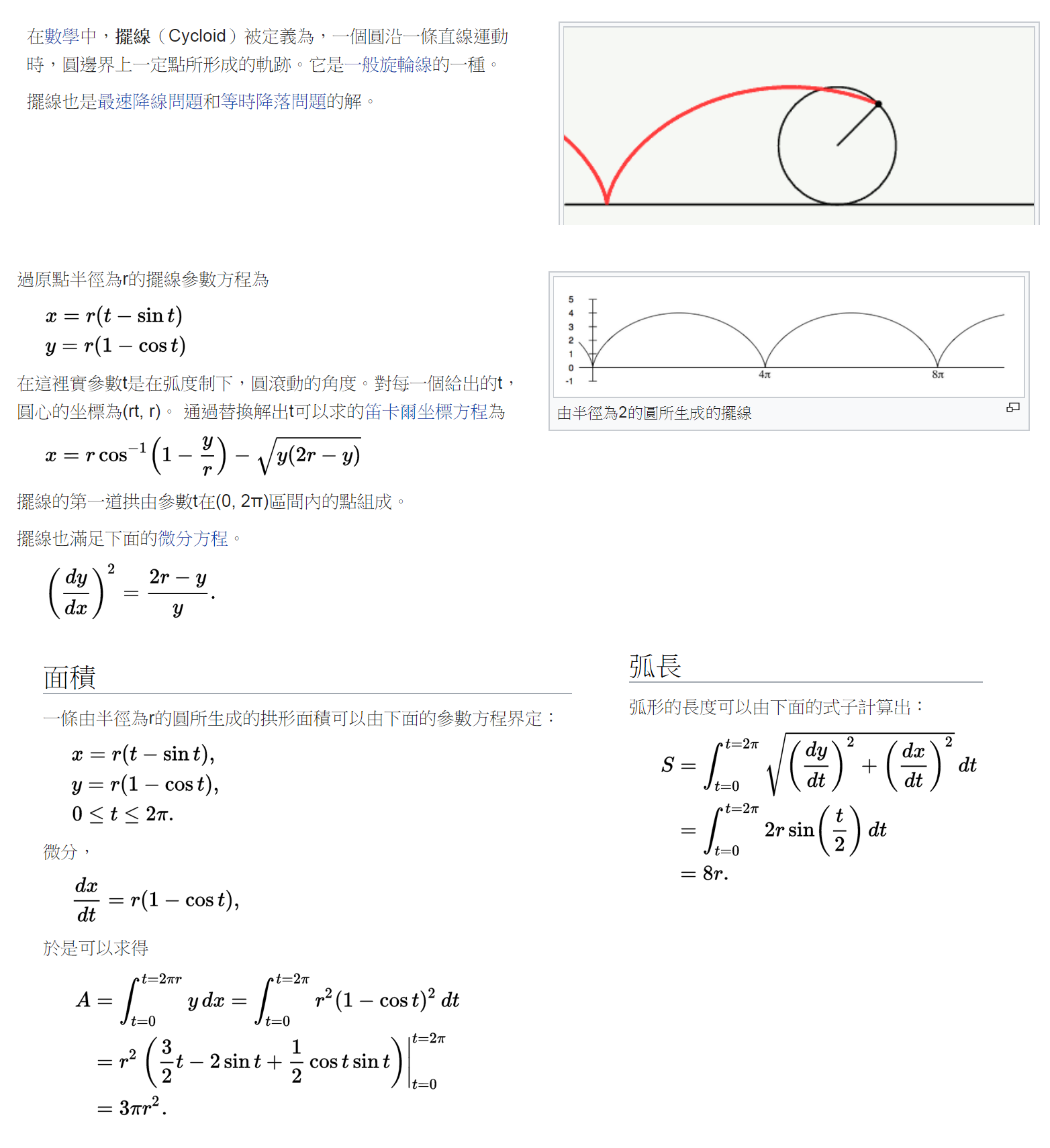
from visual import *
R=0.5; x=0.
dotv=vector(0,-R,0)
scene = display(width=1200, height=500, center=(5,0,0), background=(0.5,0.5,0))
xaxis=arrow(pos=(0,0,0),axis=(1,0,0),length=3,shaftwidth=0.05,color=color.red)
yaxis=arrow(pos=(0,0,0),axis=(0,1,0),length=3,shaftwidth=0.05,color=color.green)
zaxis=arrow(pos=(0,0,0),axis=(0,0,1),length=3,shaftwidth=0.01,color=color.blue)
floor=box(pos=(5,-R,0),length=10, height=0.1, width=1,color=(0.2,0.2,1))
f = frame()
ball=sphere(frame=f, pos=(0,0,0), radius=R, color=color.red)
dot=sphere(frame=f, pos=dotv, radius=0.1*R, color=color.yellow)
cyc=sphere(pos=dotv, radius=0.1*R, color=color.yellow, make_trail=True)
w=2.*pi/1.
v=R*w
dt=0.01
delta=w*dt
t=0.
while True:
    if(t > 3.): break
    rate(20)
    f.rotate(angle=delta, axis=(0,0,-1), origin=(0,0,0))
    x=x+v*dt
    f.pos=(x,0,0)
    cyc.pos= f.frame_to_world(dot.pos)
    t=t+dt

5. 等加角速率轉動：

就像自由落體是一個等加速度運動一樣，在轉動運動當中我們也可以用運動方程式的差分近似，來模擬一顆球的等加角速率轉動問題。在下面的例子當中，我們讓一顆球受到一個環繞著他的細線的牽引，而繞著軸心進行等加角速率運動。牽引的力量來自於細線尾端所懸掛著的一個重物，受到重力作用而向下作落體運動。在這個運動當中加速轉動是來自於細線在球的邊緣施加了一個力矩，力矩是角加速率的來源：\(\tau=I\alpha\)，I是球的轉動慣量\(I=\frac{2}{5}mR^2\)。

from visual import *
R=1; m_W=10.; m_ball=10; I=2./5.*m_ball*R**2; g=9.8; y0=-2
scene = display(width=1000, height=1000, center=(0,-10,0), background=(0.5,0.5,0))
xaxis=arrow(pos=(0,0,0),axis=(1,0,0),length=3,shaftwidth=0.05,color=color.red)
yaxis=arrow(pos=(0,0,0),axis=(0,1,0),length=3,shaftwidth=0.05,color=color.green)
zaxis=arrow(pos=(0,0,0),axis=(0,0,1),length=3,shaftwidth=0.01,color=color.blue)
weight=box(pos=(R,y0,0),length=1, height=1, width=1,color=(1,0.2,1))
arr=arrow(pos=(R,0,0),axis=(R,y0,0),shaftwidth=0.1)
f = frame(pos=(0,0,0))
ball=sphere(frame=f, pos=(0,0,0), radius=R, color=color.red)
dot=sphere(frame=f, pos=(R+0.01,0,0), radius=0.1*R, color=color.yellow)
a=m_W*g/(m_W+I/R**2)
w=0.; th=0.; y=y0; v=0.
dt=0.01
t=0.
while True:
    if(abs(y) > 20.): break
    rate(20)
    v=v-a*dt
    y=y+v*dt
    weight.pos.y += v*dt
    arr.axis=weight.pos-arr.pos
    alpha=a/R
    w=w+alpha*dt
    delta=w*dt
    th=th+delta
    f.rotate(angle=delta, axis=(0,0,-1), origin=(0,0,0))
    t=t+dt

Exercise 1.

如果你能夠充分了解上面這個程式的話，那麼請你再加入一個圓環的轉動運動到這個動畫模擬當中，而最後可以做出下面的影片所呈現的效果。記得圓環的轉動慣量是下面這個公式：\(I=mR^2\)，重物的重量仍然是10公斤，但是因為圓環的轉動慣量比較大，所以重物的負載比較大，掉落的速度會比較慢。圓環的質量1公斤、半徑1公尺，與球的質量和半徑一樣。

Exercise 2.

你可以再嘗試下面這個更為複雜的轉動模擬

6. 從斜面上滾落的球：

在下面的程式當中我們模擬了一顆球從斜面上滑落下來的運動情況，在這裡我們先定義了斜面，然後再把斜面上的球在滾動運動要滿足的運動方程式，全都放在我們的差分方程的模擬當中。

from visual import *

Lx=10.; R=0.5; g=9.8; th=radians(30.); beta=0.5; x=0.
dotv=vector(0,0.4,0.3)
scene2 = display(width=1000, height=1000, center=(-Lx/2,-3,0), background=(1,1,1))
xaxis=arrow(pos=(0,0,0),axis=(1,0,0),length=3,shaftwidth=0.05,color=color.red)
yaxis=arrow(pos=(0,0,0),axis=(0,1,0),length=3,shaftwidth=0.05,color=color.green)
zaxis=arrow(pos=(0,0,0),axis=(0,0,1),length=3,shaftwidth=0.01,color=color.blue)
ramp=box(axis=(cos(th),sin(th),0),pos=(-Lx/2,0,0),length=10, height=0.01, width=1,color=(0.2,0.2,1))
ramp.pos.y=-Lx/2*sin(th)-R*2.

bp=vector(0,0,0)
f = frame(pos=(0,0,0))
ball=sphere(frame=f, pos=bp, radius=R, color=color.red)
dot=sphere(frame=f, pos=bp+dotv, radius=R/5., color=color.yellow)
ball2=sphere(pos=bp, radius=R, color=color.red
             ,make_trail=True,trail_type="points", interval=10)

w=10.
vs=R*w
s=-5.
dt=0.01
t=0.
while True:
	if(t > 4.): break
	rate(20)
	ac=-g*sin(th)/(1.+beta)
	alpha=ac/R
	w=w+alpha*dt
	delta=w*dt
	vs=vs+ac*dt
	s=s+vs*dt
	f.rotate(angle=delta, axis=(0,0,-1), origin=(0,0,0))
	ballpos=vector(s*cos(th),s*sin(th),0)
	f.pos=ballpos
	ball2.pos=ballpos
	t=t+dt

7. 角動量守恆：

最下面這個模擬當中我們實現了角動量守恆的概念，棒子的長度隨著時間等速率變長的過程當中，為了維持角動量守恆，轉動的角速率會變慢。

from visual import *
g=9.8; R=0.5; H=1.2;M=5; MA=5
scene2 = display(width=800, height=800, center=(0,0,0), background=(0.5,0.5,0))
yaxis=arrow(pos=(0,0,0),axis=(0,1,0),length=3,shaftwidth=0.05,color=color.green)
floor1=box(length=10,height=0.02,width=2,pos=(4,-R,0))
f = frame()
sphere1=sphere(frame=f, pos=(0,0,0), radius=R, color=color.red)
arm=cylinder(frame=f, pos=(-H/2,0,0), radius=R/2., axis=(H,0,0)
		,color=color.white)
omega=100.
Imom=2./5.*M*R**2+MA*H**2/12.
Lmom0=Imom*omega
dt=0.001
while True:
    rate(100)
    dth=omega*dt
    f.rotate(angle=dth, axis=(0,1,0), origin=(f.pos))
    H=H+1.5*dt
    arm.pos=vector(-H/2,0,0)
    arm.axis=vector(H,0,0)
    Imom=2./5.*M*R**2+MA*H**2/12.
    omega=Lmom0/Imom

8. 保齡球的運動：

在下面這個程式當中我們模擬一個保齡球，從接觸到地面開始，先是摩擦造成的滑動現象，在地面上滑動一段距離之後，就會進入滾動的模式，也就是轉動的距離等於質心移動的距離，所謂的滾動條件: \(s=r\theta\)。

from visual import *
R=0.8; m=0.5; Lx=40
scene2 = display(width=1200, height=600,
                 center=(Lx/2.,0,0), background=(0.5,0.5,0))
xaxis=arrow(pos=(0,0,0),axis=(1,0,0),length=3,shaftwidth=0.05,color=color.red)
yaxis=arrow(pos=(0,0,0),axis=(0,1,0),length=3,shaftwidth=0.05,color=color.green)
zaxis=arrow(pos=(0,0,0),axis=(0,0,1),length=3,shaftwidth=0.01,color=color.blue)
floor1=box(length=Lx,height=0.02,width=2,pos=(Lx/2,-R,0))

f1 = frame()
sphere1=sphere(frame=f1, pos=(0,0,0), radius=R, color=color.red)
sphere2=sphere(frame=f1, pos=(R,0,0), radius=0.001, color=color.white)
spot1=sphere(pos=(R,0,0), radius=0.10, color=color.white,make_trail=True)

I=2./5.*m*R**2
fk=1.2
w1=0.
x1=0.; v1=15.; th1=0.; dt=0.01; t=0.; nn=0
while True:
    rate(10)
    if(x1 > 40.):   break
    if(R*w1 < v1):
        a1=-fk/m
        alpha1=R*fk/I
    else:
        nn=nn+1
        if(nn==1): spot2=sphere(pos=spot1.pos, radius=0.20, color=color.black)
        a1=0.
        alpha1=0.
    x1=x1+v1*dt
    v1=v1+a1*dt
    w1=w1+alpha1*dt
    dth1=w1*dt
    f1.rotate(angle=dth1, axis=(0,0,-1), origin=(x1,0,0))
    f1.pos=vector(x1,0,0)
    wspot1_pos = f1.frame_to_world(sphere2.pos)
    spot1.pos=wspot1_pos
    th1=th1+dth1
    t=t+dt