高斯定律
物理學的主要目標之一是找到解決複雜問題的簡單方法,實現這一目標的主要物理學工具之一是使用對稱性。例如,在求帶電環,帶電棒和帶電平面的電場時,我們先考慮環和棒中帶電元素的產生的電場的幾何結構。然後我們簡化了計算,使用對稱性以丟棄向量的垂直分量,把向量的計算簡化為純量的計算,這為我們節省了一些工作。對於某些涉及對稱性的電荷分佈,我們可以通過使用由德國數學、物理學家高斯(Gauss, 1777-1855)開發的以其人為名的高斯定律來節省許多的計算工作。高斯定律並不直接對電荷產生的電場做積分,而是考慮一假想封閉表面(高斯表面)與電荷分佈的電場之間的關聯性。這種所謂的高斯面可以是任何形狀,但是為簡化我們對電場的計算,高斯面的形狀是與電荷分佈相稱的形狀。例如,如果電荷均勻分佈在球體上,我們用球面作為高斯面包圍帶電球體,對於帶電的棒子我們會選擇一個圓柱體來包著帶電棒子上的電荷。我們也可以反過來使用高斯定律:如果我們知道高斯表面上的電場,我們可以找到被高斯面包圍的淨電荷。考慮下面的例子,假設有一個球面作為高斯面,面上的電場向量都從球心徑向向外指向並且具有相等的大小。高斯定律立即告訴我們,球面必須包含一個淨正電荷,該電荷可能是點電荷或是呈球形分佈。然而,為了計算有多少電荷被包圍,我們需要一種方法來計算有多少電場被高斯面截獲。一個表面截獲電場的這種度量稱為電通量,我們就來討論電通量的定義和應用。
電場的電通量
▶電場電通量解說影片
電通量
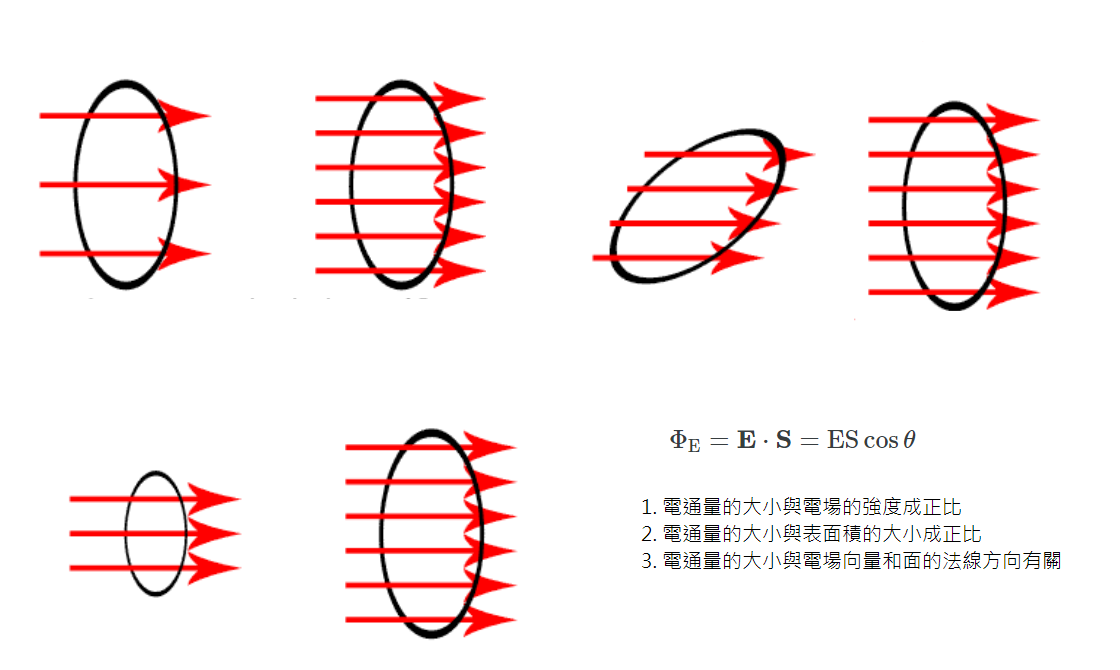
“通量”一詞來自拉丁語,意思是“流動”,例如我們考慮循環空氣的流量,那麼這個流量的含義是具體的。我們可以想像在空氣流動的氣場中放置一個圓環,試圖計算單位時間內有多少氣體會通過這個圓環,也就是氣體的流量。我們可以為通過環路的氣流中的每個點分配一個速度向量,因為所有這些向量的合成是一個速度場, 透過速度場向量與圓環對應的法線向量取向量內積,再對所有面積求和就可以得到整體氣體通量,這就是計算氣體通量的標準方法。我們可以把氣體通量的概念抽象化,對所有的向量場,即便是沒有實體物質的電場,以電荷所發出的電場來取代氣體的速度場,就可以定義電通量,並且用相同的數學方法來計算給定的面的電通量。所以電通量基本上就是的電場與面的成績。電荷的周圍充斥著電場。若以圖形表示,該電場可以被表示為從一個點(電荷)散開的輻射線,稱為電場線或電力線。而這些線的密度與電場強度呈正相關,稱為電通量密度,也就是每單位面積的電力線數目。因此,電通量與穿過表面的電場線的總數成正比。為了簡化計算,通常在計算上會選取垂直於電力線的表面。如果電場為一均勻電場,則通過所選面積 \( \mathbf {S} \) 的表面的通量為 \[ \Phi_{E}=\mathbf{E} \cdot \mathbf{S} =ES \cos \theta \] 其中\( \mathbf{E} \)為電場(單位為 V/m )、\(E\)為電場強度、 \(S\) 為表面面積、 \( \theta\) 為電場線與 \(S\) 的法線之間的夾角。
|
|
如果電場為一非均勻電場,則通常會將此一較大面積的電通量分割,改取一小塊面積 \( d\mathbf{S}\) 上的電通量 \(d\Phi_{E}\) \[ d\Phi_{E}=\mathbf{E} \cdot d\mathbf{S}\] (電場 \(\mathbf {E}\)乘以垂直於所選面積表面的分量)。因此,表面 \(S\) 上的電通量可由表面積分得到:
\(\Phi_{E}=\iint_{S} \mathbf{E} \cdot d\mathbf{S}\)
其中 \(\mathbf{E}\)是電場,\(d\mathbf{S}\)是閉合表面\(S\)上的微小面積,其方向定義為表面法線朝外。電通量的單位為伏特米(V·m)。
例題1:圓柱高斯面
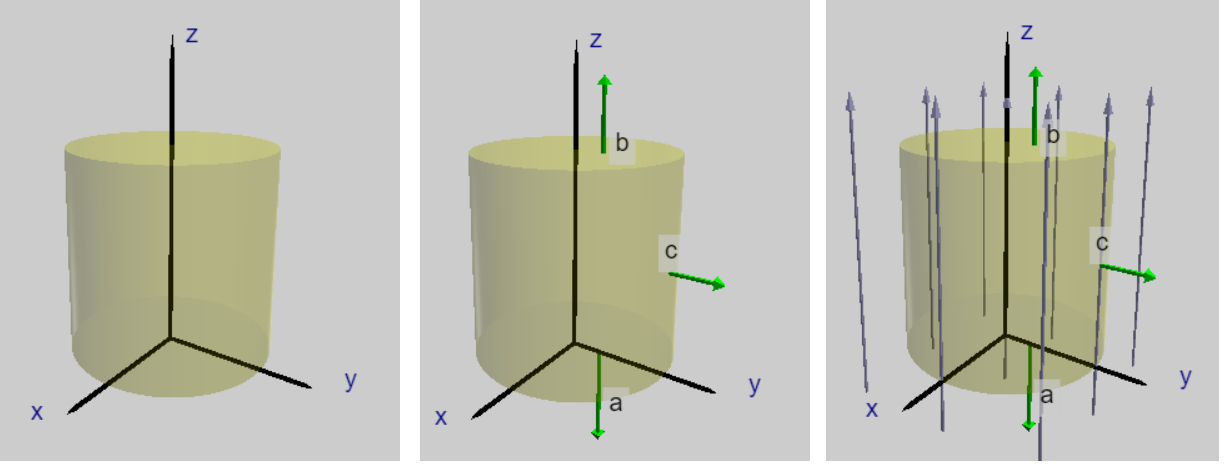
例題2:非均勻電場的電通量
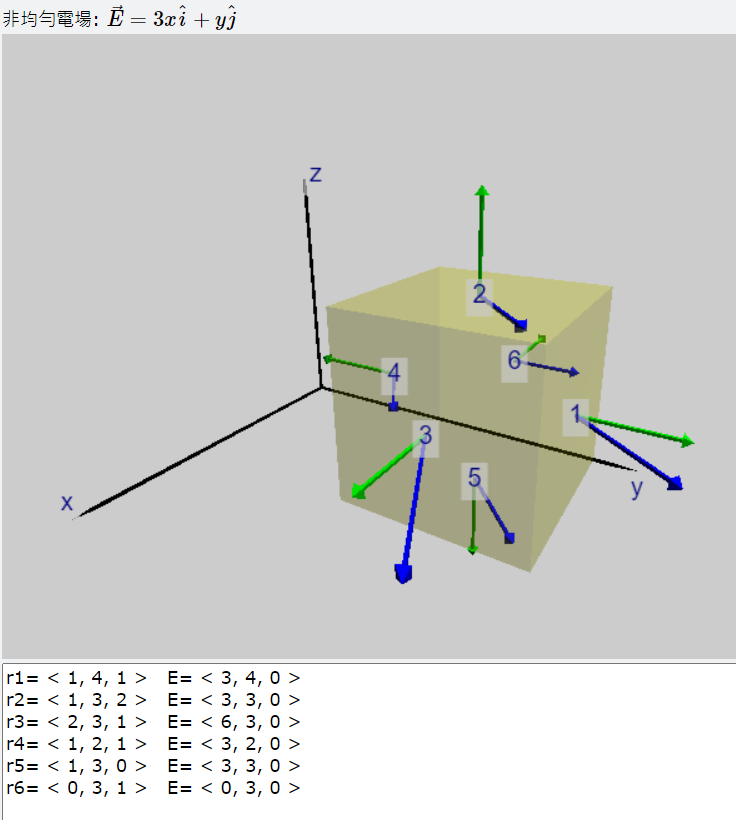 在這個例題當中我們來考慮一個非均勻電場的電通量。在這個問題中我們的高斯面是一個邊長\(L\)的立方體,立方體的六個面形成的封閉曲面就是我們的高斯面。電場並非均勻,向量場的函數如下:\[\vec{E}=3x \hat{i} + y\hat{j}\]
立方體的位置是向+y軸方向平移,左邊的面(編號4的面)的\(y\)座標是\(L\),\(y_4=L\),右邊的面(編號1的面)的\(y\)座標為\(y_1=2L\)。在圖形中我們分別對6個面取了6個點,計算電場在這個6個點的向量,並且在圖形中畫出電場向量和這個面的法線方向,我們可以對每一個面計算出電通量,分別如下:
在這個例題當中我們來考慮一個非均勻電場的電通量。在這個問題中我們的高斯面是一個邊長\(L\)的立方體,立方體的六個面形成的封閉曲面就是我們的高斯面。電場並非均勻,向量場的函數如下:\[\vec{E}=3x \hat{i} + y\hat{j}\]
立方體的位置是向+y軸方向平移,左邊的面(編號4的面)的\(y\)座標是\(L\),\(y_4=L\),右邊的面(編號1的面)的\(y\)座標為\(y_1=2L\)。在圖形中我們分別對6個面取了6個點,計算電場在這個6個點的向量,並且在圖形中畫出電場向量和這個面的法線方向,我們可以對每一個面計算出電通量,分別如下:\(\Phi_1=16 ; \quad \Phi_2=0 \)
\(\Phi_3=24 ; \quad \Phi_4=-8 \)
\(\Phi_5=0 ; \quad \Phi_6=0 \)
\(\Phi=\sum_i \Phi_i=\)
我們考慮編號1的面。這個面上的所有的點的y座標都是\(2L\),法線方向是(0,1,0),考慮法線向量與電場的向量內積,我們只需考慮電場的y分量,\(E_y=y\)與座標點的y分量有關,面上的所有的點的y座標都是\(2L\),因此所有的點的內積的值都是\(\vec{E} \cdot \hat{n}=y=2L\),正方形的面積為\(A=L^2=4\),這個面的電通量貢獻就是:\(\Phi_1=(2L)A=2L(L^2)=2L^3=16\)。同樣的分析方法我們可以得到其他5個面的電通量。
高斯定律
高斯定律將(閉合)高斯表面上各點處的電場與該表面包圍的淨電荷聯繫起來。高斯定律(Gauss' law)表明在
如果電場為一非均勻電場,則通常會將此一較大面積的電通量分割,改取一小塊面積 \( d\mathbf{S}\) 上的電通量 \(d\Phi_{E}\) \[ d\Phi_{E}=\mathbf{E} \cdot \mathrm{d}\mathbf{S}\] (電場 \(\mathbf {E}\)乘以垂直於所選面積表面的分量)。因此,表面 \(S\) 上的電通量可由表面積分得到:
\(\Phi_{E}=\oint_{S} \mathrm{d}\Phi= \oint_{S} \mathbf{E} \cdot \mathrm{d} \mathbf{S}\)
其中 \(\mathbf{E}\)是電場,\(\mathrm{d} \mathbf{S}\)是閉合表面\(S\)上的微小面積,其方向定義為表面法線朝外。
\(\varepsilon_{0}\)是介電常數(為一通用常數,也稱為真空中電容率或真空介電常數 )。\( \varepsilon _{0}\approx 8.85...\times 10^{-12} \text{F/m}\)。上式以積分形式呈現被稱為電場高斯定律,是四個馬克士威方程式之一。
此方程式是高斯在1835年提出的,但直到1867年才發布。因為數學上的相似性,高斯定律也可以應用於其它由反平方定律決定的物理量,例如重力或者輻照度。
電偶極電場的電通量
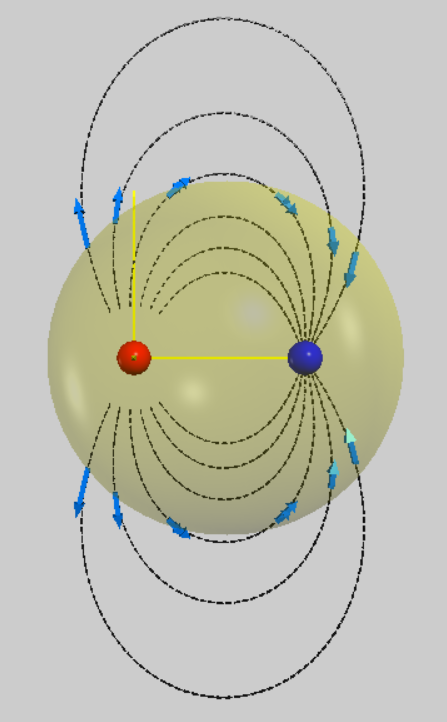
以一個圓柱體的高斯面包著一個直線電荷計算高斯面的電通量:
\[\Phi=E(2 \pi rL)=\dfrac{\lambda L}{\varepsilon_0}; \quad E=\dfrac{\lambda}{2 \pi \varepsilon_0 r}\]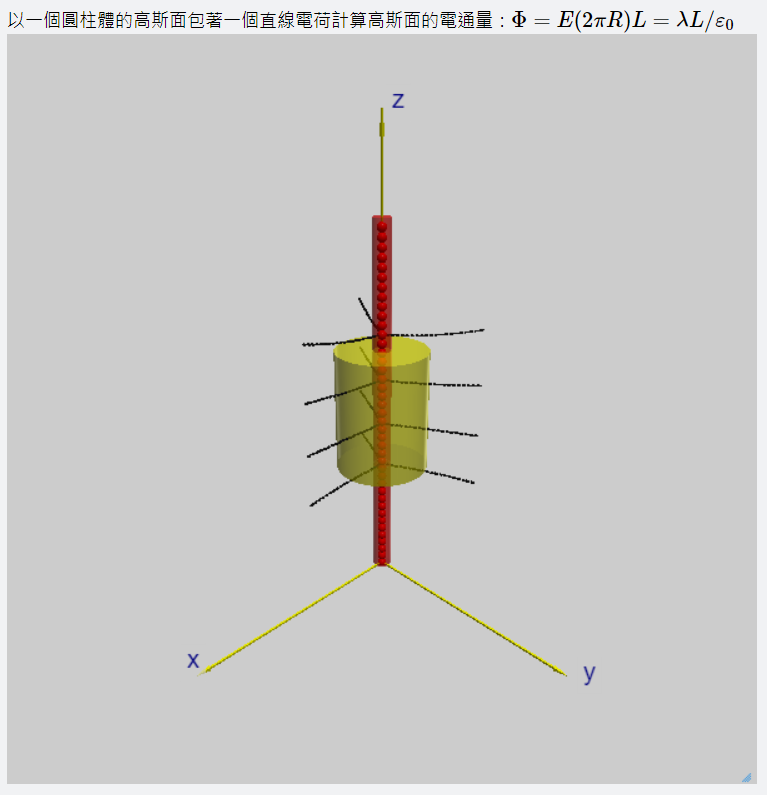
以一個圓柱體的高斯面包著一個帶電的平面,計算高斯面的電通量:
\[\Phi=2EA=\sigma A/\varepsilon_0; \quad E=\sigma/(2 \varepsilon_0) \]: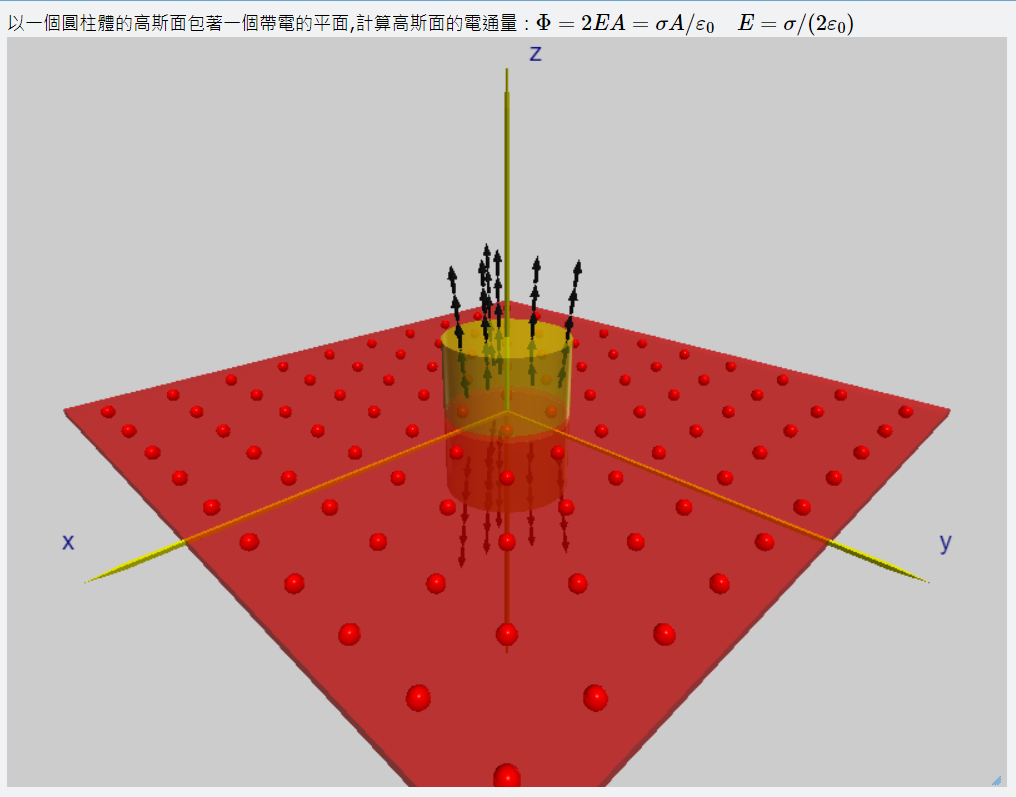
範例-1:圓柱體表面電通量
|
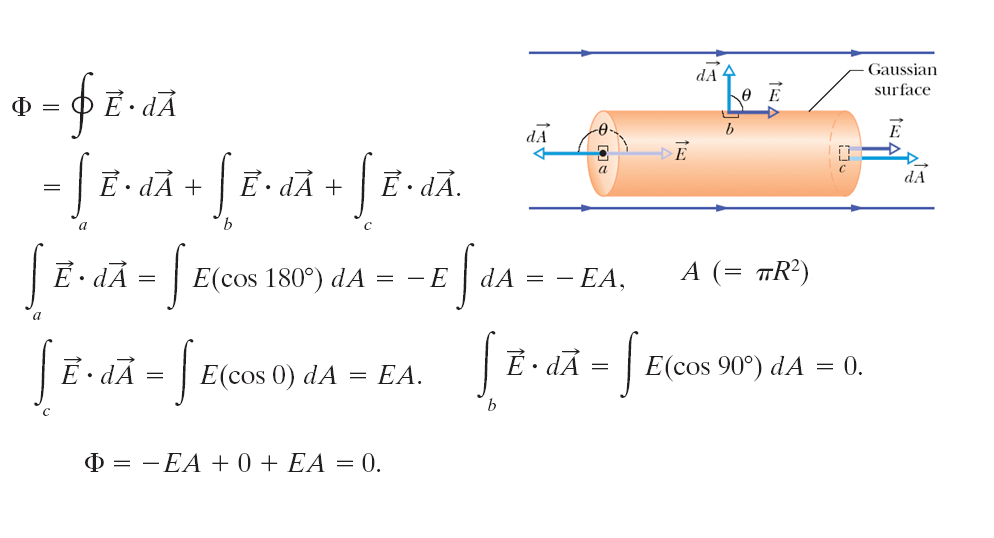
The figure shows a Gaussian surface in the form of a cylinder of radius \(R\) immersed in a uniform electric field \(\vec{E}\), with the cylinder axis parallel to the field. What is the flux \(\Phi\) of the electric field through this closed surface? 該圖顯示了一個半徑為 \(R\) 的圓柱體形式的高斯表面,該圓柱體浸入均勻的電場 \(\vec{E}\) 中,圓柱軸平行於電場。 通過這個封閉表面的電場通量 \(\Phi\) 是多少? |
|
範例-2:立方體表面電通量
|
A nonuniform electric field given by \(\vec{E}=3.0x \,\hat{i} + 4.0 \, \hat{j}\) pierces the Gaussian cube shown in the figure. (\(E\) is in newtons per coulomb and \(x\) is in meters.) What is the electric flux through the right face, the left face, and the top face? 由 \(\vec{E}=3.0x \,\hat{i} + 4.0 \, \hat{j}\) 給出的非均勻電場穿過圖中所示的高斯立方體。 (\(E\) 以牛頓每庫侖為單位,\(x\) 以米為單位。)通過右面、左面和頂面的電通量是多少? |

|
範例-3:高斯定律
|
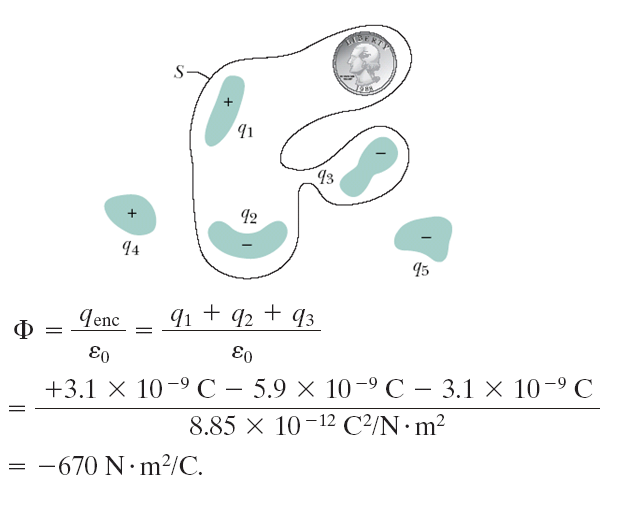
The figure shows five charged lumps of plastic and an electrically neutral coin. The cross section of a Gaussian surface \(S\) is indicated. What is the net electric flux through the surface if
\[q_1= q_4=+3.1 \,\text{nC}, q_2=q_5=-5.9\,\text{nC}, \, q_3=-3.1 \,\text{nC}?\] 該圖顯示了五個帶電的塑料塊和一個電中性硬幣。 表示了高斯曲面 \(S\) 的橫截面。 如果 \[q_1= q_4=+3.1 \,\text{nC}, q_2=q_5=-5.9\,\text{nC}, \, q_3=-3.1 \,\text{nC}?\] 則通過表面的淨電通量是多少? |
|
範例-4:立方體表面電通量
|
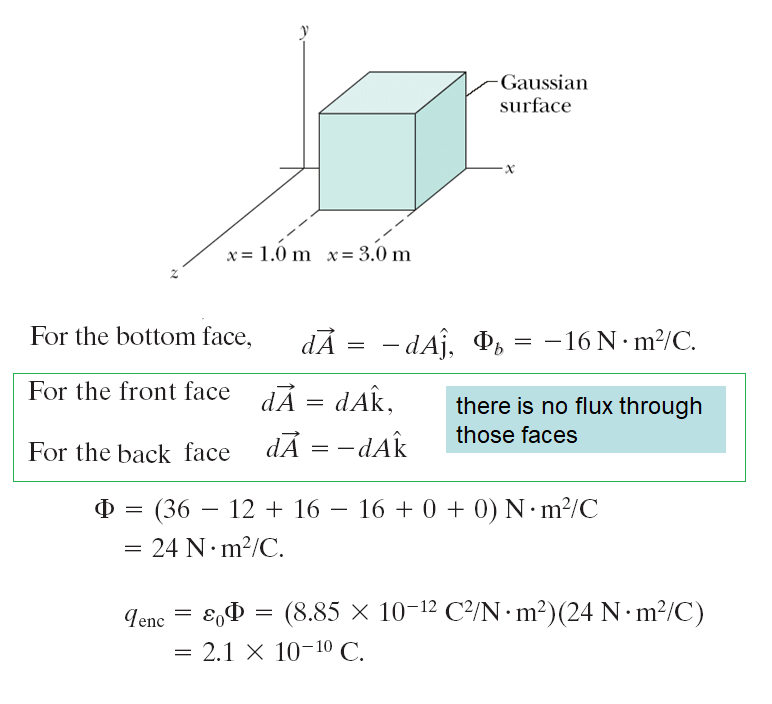
A nonuniform electric field given by \(\vec{E}=3.0x \,\hat{i} + 4.0 \, \hat{j}\) pierces the Gaussian cube shown in the figure. (\(E\) is in newtons per coulomb and \(x\) is in meters.) What is the net charge enclosed by the Gaussian cube? 由 \(\vec{E}=3.0x \,\hat{i} + 4.0 \, \hat{j}\) 給出的非均勻電場穿過圖中所示的高斯立方體。 (\(E\) 的單位是牛頓每庫侖,\(x\) 的單位是米。)高斯立方體包圍的淨電荷是多少? |
|
範例-5:帶電金屬球殼的電場分布
|
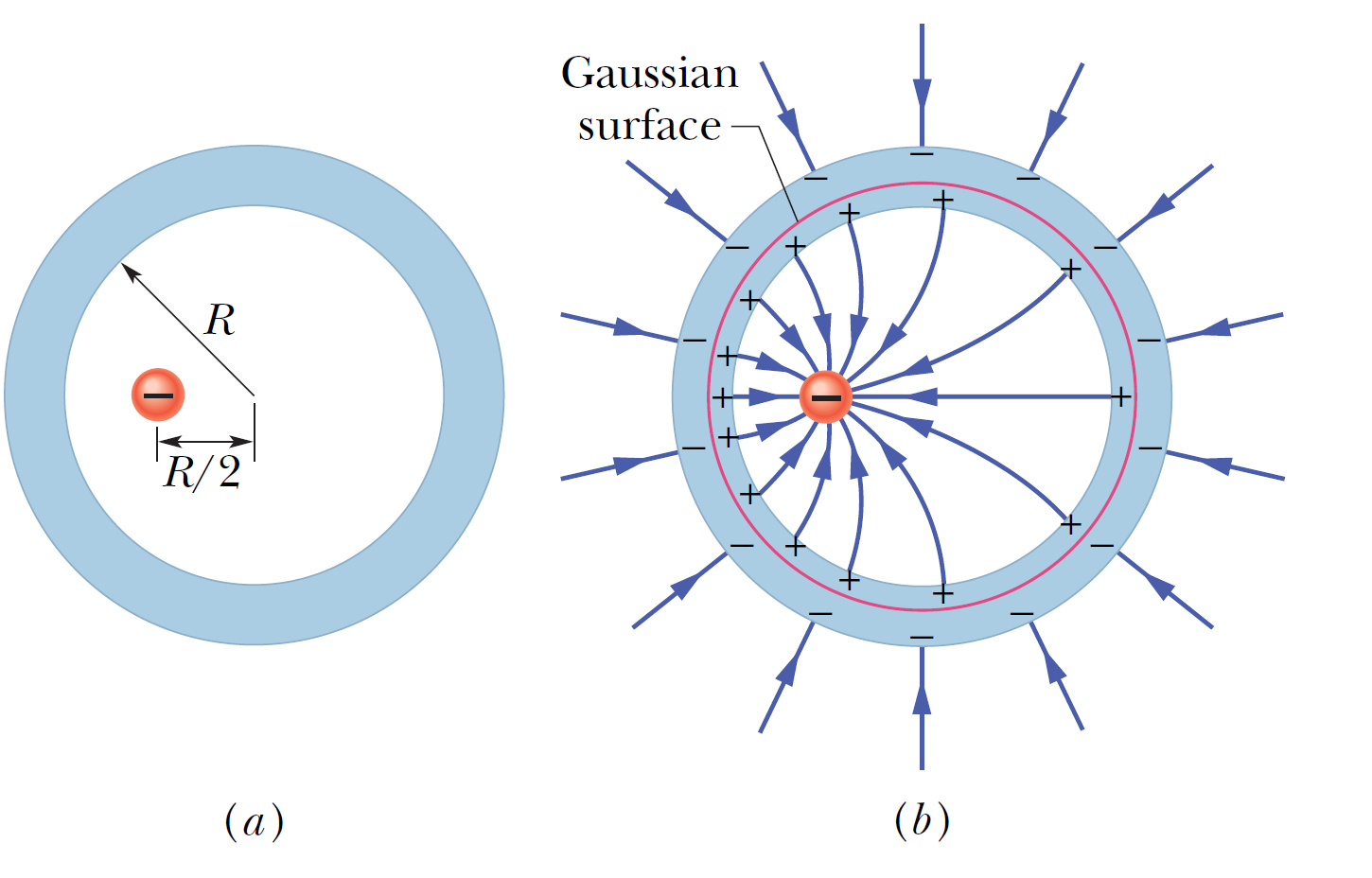
The figure (a) shows a cross section of a spherical metal shell of inner radius \(R\). A point charge of \(5.0 \, \mu\)C is located at a distance \(R/2\) from the center of the shell. If the shell is electrically neutral, what are the (induced) charges on its inner and outer surfaces? Are those charges uniformly distributed? What is the field pattern inside and outside the shell? 圖 (a) 顯示了內半徑為 \(R\) 的球形金屬殼的橫截面。 \(5.0\, \mu\)C 的點電荷位於距離殼中心 \(R/2\) 處。 如果殼是電中性的,它的內外表面的(感應)電荷是多少? 這些費用是均勻分佈的嗎? 外殼內外的場模式是什麼? |
 |
授課教師
陳永忠 ycchen@thu.edu.tw