電位
庫倫靜電力是一種保守力,位能和保守力息息相關是非常有用的一種物理觀念。靜電位能是電荷系統所擁有的能量,這種能量可視為外力對抗電荷間的庫倫力所做的功,並以位能的形式儲存在電荷系統內,靜電位能之於庫倫靜電力,相似於重力位能之於萬有引力。萬有引力有重力場的概念,而庫倫靜電力也有電場的概念。和重力場息息相關的一個概念就是重力位。同樣的,和電場相關的一個概念就是電位,從電位差與電場間的關係我們可以了解等位面與電力線之間的關係。本單元將定義電荷系統的靜電位能和電位,並分析電位與電場間的關係。如何計算一個電荷分佈系統的電位差及電位,並從而計算電場。靜電平衡條件下的帶電導體具有一些特殊的電學性質,本單元也將引用電位差與電場的概念,討論導體的尖端效應與靜電屏蔽等現象。電位能差及電位能
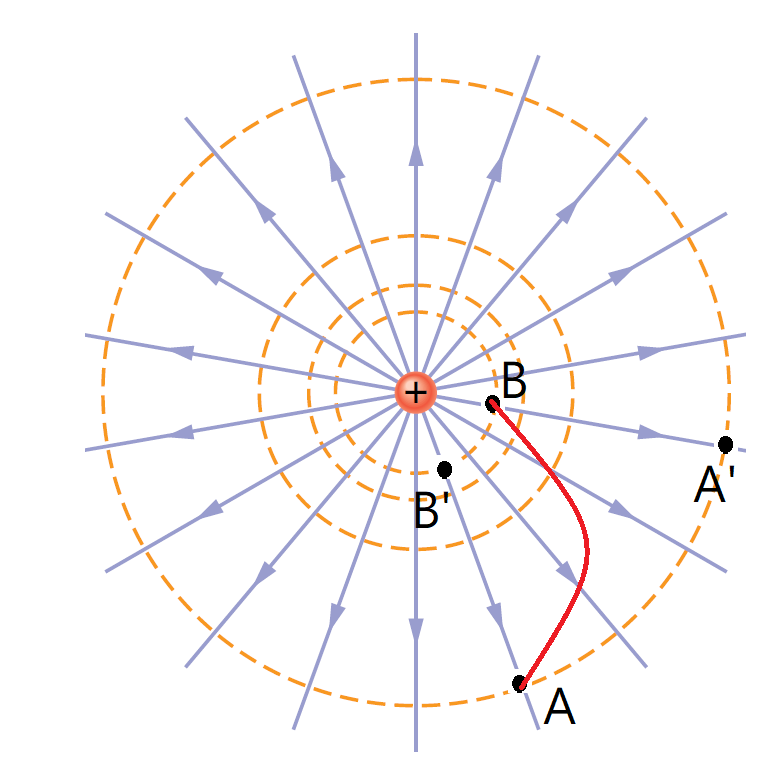 萬有引力是一種保守力,靜電力遵守庫倫定律,而庫倫定律在數學形式上類似於牛頓的萬有引力定律,因此庫倫靜電力也是一種保守力。並且因為疊加原理適用於庫倫靜電力,因此一個點電荷的電場所擁有的特性,一般都能加以推廣應用到任意的電荷分佈。為了簡化討論,我們就從單一點電荷來討論空間中的電場和電位。假設有一個點電荷\(q\)固定於空間某一點\(O\),並且將這個點設定為空間座標的原點,我們假設\(q \gt 0\)。在圖中我們描繪出此電和周圍的一些電力線。考慮置放在圖中\(A\)點的一個測試點電荷\(q_0\),由於電荷\(q, \, q_0\)間的庫倫力\(F_e\)之作用,因此要將\(q_0\)停留在\(A\)點上必須對之施加一個外力\(F_{ext}\)來平衡此庫倫力。現在讓我們將\(q_0\)從\(A\)點沿路徑\(C\)移到另一點\(B\),並計算外力\(F_{ext}\)對抗庫倫力\(F_e\)所必須做的功。假設在此過程中點電荷\(q_0\)處於力的平衡狀態,外力剛好抵銷庫倫力\(\vec{F}_{ext}=-\vec{F}_e=-q_0 \vec{E}\),外力對\(q_0\)沿路徑\(C\)做一小位移,\(d\vec{l}\)所需做的功為\(dW=-q_0 \vec{E} \cdot d\vec{l}\),其中\(\vec{E}\)為電場。路徑C是以A為起點B為終點,沿著這條曲線外力對測試電荷所做的功可以透過路徑積分得到,也就是下面的積分公式:
\[W_C=\int_C \vec{F}_{ext} \cdot d\vec{l} = -q_0 \int_C \vec{E} \cdot d\vec{l} \]
起點與終點分別是A點和B點的路徑有無窮多個,我們還可以考慮下面兩個特別的路徑。第一個是從A點沿著同心圓到達A'點,再從A'點沿著半徑方向,指向原點到達B點。對這條路徑來做功的計算,我們不難發現從A到A'地路徑方向與電場方向垂直(\(d\vec{l} \perp \vec{E}\)),因此這段路徑的積分為0,沒有貢獻。
同樣的我們可以考慮另外一個路徑,從A沿著半徑方向指向圓心,到達B'點,再從B'點沿著同心圓的路徑到達B點,同理B到B'的這段圓弧的路徑積分沒有貢獻,徑向路徑(\(A \rightarrow B'\))上的積分與前一個路徑中(\(A' \rightarrow B\))的路徑積分相同,因此這兩個路徑積分會給出相同的功值(\(W_{A-A'-B}=W_{A-B'-B}\))。前面的路徑C也可以分段拆解成這兩種路徑積分的合成,因此沿路徑C所作的路徑積分也會得到相同的數值。透過這些觀察我們不難證明只要起點與終點固定為A和B,無論選擇什麼樣的路徑,庫倫靜電力所做的功值全都相同。因此我們可以類比重力一樣,定義點A與B之間存在位能差,這個差值只跟A,B兩點的座標有關,與所選擇積分的路徑無關,這就是電位能差的基本定義:
\[dU=dW=\vec{F}_{ext} \cdot d\vec{l}=-q_0 \vec{E} \cdot d\vec{l}\]
\[\Delta U= \int_i^f q_0 \vec{E} \cdot d\vec{l}。 \]
具有這種做功的大小與路徑無關的特性的力稱為保守力。如果外力做正功(電力做負功)則靜電位能增加,反之則減少;若外力所做的功為零,則靜電位能沒有改變,\(\Delta U=0\)。
萬有引力是一種保守力,靜電力遵守庫倫定律,而庫倫定律在數學形式上類似於牛頓的萬有引力定律,因此庫倫靜電力也是一種保守力。並且因為疊加原理適用於庫倫靜電力,因此一個點電荷的電場所擁有的特性,一般都能加以推廣應用到任意的電荷分佈。為了簡化討論,我們就從單一點電荷來討論空間中的電場和電位。假設有一個點電荷\(q\)固定於空間某一點\(O\),並且將這個點設定為空間座標的原點,我們假設\(q \gt 0\)。在圖中我們描繪出此電和周圍的一些電力線。考慮置放在圖中\(A\)點的一個測試點電荷\(q_0\),由於電荷\(q, \, q_0\)間的庫倫力\(F_e\)之作用,因此要將\(q_0\)停留在\(A\)點上必須對之施加一個外力\(F_{ext}\)來平衡此庫倫力。現在讓我們將\(q_0\)從\(A\)點沿路徑\(C\)移到另一點\(B\),並計算外力\(F_{ext}\)對抗庫倫力\(F_e\)所必須做的功。假設在此過程中點電荷\(q_0\)處於力的平衡狀態,外力剛好抵銷庫倫力\(\vec{F}_{ext}=-\vec{F}_e=-q_0 \vec{E}\),外力對\(q_0\)沿路徑\(C\)做一小位移,\(d\vec{l}\)所需做的功為\(dW=-q_0 \vec{E} \cdot d\vec{l}\),其中\(\vec{E}\)為電場。路徑C是以A為起點B為終點,沿著這條曲線外力對測試電荷所做的功可以透過路徑積分得到,也就是下面的積分公式:
\[W_C=\int_C \vec{F}_{ext} \cdot d\vec{l} = -q_0 \int_C \vec{E} \cdot d\vec{l} \]
起點與終點分別是A點和B點的路徑有無窮多個,我們還可以考慮下面兩個特別的路徑。第一個是從A點沿著同心圓到達A'點,再從A'點沿著半徑方向,指向原點到達B點。對這條路徑來做功的計算,我們不難發現從A到A'地路徑方向與電場方向垂直(\(d\vec{l} \perp \vec{E}\)),因此這段路徑的積分為0,沒有貢獻。
同樣的我們可以考慮另外一個路徑,從A沿著半徑方向指向圓心,到達B'點,再從B'點沿著同心圓的路徑到達B點,同理B到B'的這段圓弧的路徑積分沒有貢獻,徑向路徑(\(A \rightarrow B'\))上的積分與前一個路徑中(\(A' \rightarrow B\))的路徑積分相同,因此這兩個路徑積分會給出相同的功值(\(W_{A-A'-B}=W_{A-B'-B}\))。前面的路徑C也可以分段拆解成這兩種路徑積分的合成,因此沿路徑C所作的路徑積分也會得到相同的數值。透過這些觀察我們不難證明只要起點與終點固定為A和B,無論選擇什麼樣的路徑,庫倫靜電力所做的功值全都相同。因此我們可以類比重力一樣,定義點A與B之間存在位能差,這個差值只跟A,B兩點的座標有關,與所選擇積分的路徑無關,這就是電位能差的基本定義:
\[dU=dW=\vec{F}_{ext} \cdot d\vec{l}=-q_0 \vec{E} \cdot d\vec{l}\]
\[\Delta U= \int_i^f q_0 \vec{E} \cdot d\vec{l}。 \]
具有這種做功的大小與路徑無關的特性的力稱為保守力。如果外力做正功(電力做負功)則靜電位能增加,反之則減少;若外力所做的功為零,則靜電位能沒有改變,\(\Delta U=0\)。上面我們定義了A,B兩點之間的位能差\(\Delta U\),但是我們並未定義A點的位能的絕對數值,因為我們並未選定位能的零點在何處。在習慣上,科學家選擇距離所有電荷無窮遠處的電位能為零,在這個選擇下A點和B點的位能值就有了明確的定義。但是這個選擇並不是唯一的,我們可以針對不同的問題、不同的電荷組態來選擇位能的0點,用以簡化我們的計算。例如在下面要討論的帶電平行面板,我們會選擇靠近其中一個面板的電位為0。根據電位能差的定義我們可以很快的計算出A點的電位能,也就是我們將一個測試電荷\(q_0\)沿著半徑方向的直線,從無窮遠處移動到A點,電場所做的功就是A點的電位能,其公式如下(假設A點到點電荷也就是座標原點的距離為\(r_A\)): \[U_A-U_{\infty}=- \int_\infty^A q_0 \vec{E} \cdot \text{d}\vec{l} = -q_0 \int_\infty^{r_A} \dfrac{kq q_0}{r^2}(-|\text{d}r|) \\ = -q_0 \int_\infty^{r_A} \dfrac{kq q_0}{r^2} \, \text{d}r= -q_0 \left[ -\dfrac{kq q_0}{r} \right]_{\infty}^{r_A}= \dfrac{k q q_0}{r_A} - \dfrac{k q q_0}{\infty} \\ \] \[ U_{\infty}=0 \rightarrow U_A= \dfrac{k q q_0}{r_A} =\dfrac{q q_0}{4 \pi \varepsilon_0 r_A} \]
電位差及電位
就如同我們把庫侖力除以測試電荷的電量來定義電場一樣,我們把靜電位能差\(\Delta U\)除以測試電荷的電量\(q_0\)用來定義電位差\(\Delta V\): \[\Delta V=\dfrac{\Delta U}{q_0}=-\frac{W_e}{q_0}\] \(W_e\)是電場所做的功等於負的靜電位能差:\(W_e=-\Delta U\)。如果我們定義距離電荷無窮遠處的電位能為0,那麼無窮遠處的電位也是0。我們就可以對空間中任何一點定義該位置的電位: \[V(x,y,z)=\dfrac{U(x,y,z)}{q_0}\] 對放置在座標原點的點電荷\(q\)而言,空間中任何一點\(P=(x,y,z)\)的電位就可寫成與點電荷距離的一次方成反比的電位公式: \[ V_P (x,y,z)=\dfrac{kq}{r}, \quad r=\sqrt{x^2+y^2+z^2}\] \[ V_P (x,y,z)=\dfrac{kq}{\sqrt{x^2+y^2+z^2}} \] 從這個公式我們知道,對一個帶正電的點電荷而言,空間中的電位會隨著遠離正電荷的距離增加而漸漸減少;從遠方靠近正電荷的時候,電位會不停的增加。也就是靠近正電荷的電位較高,遠離正電荷的電位較低。相對地,對負電荷而言靠近負電荷電位比較低,遠方的電位比較高。有許多的電荷的電位
同樣的,如果我們在空間中有兩個點電荷\(q_1, q_2\),座標位置向量分別為\(\vec{r}_1=(x_1,y_1,z_1)\), \(\vec{r}_2=(x_2,y_2,z_2)\),並且定義無窮遠處的電位為0,那麼在\(P\)點的電位可以透過從無窮遠處將一個測試電荷移動到\(P\)點所需做的功,來定義\(P\)點的電位。當我們要計算功的時候,我們會用到線性疊加原則。分別對兩個電荷做路徑積分,因此\(P\)點的電位,最後會是個別的電荷的距離反比定律所得到的電位之和: \[ V_P (x,y,z)=\dfrac{kq_1}{r_1}+\dfrac{kq_2}{r_2}, \\ r_1=\sqrt{(x-x_1)^2+(y-y_1)^2+(z-z_1)^2} \\ r_2=\sqrt{(x-x_2)^2+(y-y_2)^2+(z-z_2)^2}\] 更進一步的推廣,空間中如果有N個電荷,電荷的電量和放置的位置分別是\(q_i\)和\(\vec{r}_i\),在坐標\(\vec{r}=(x,y,z)\)處的電位可以從下面的公司做計算: \[ V_P (x,y,z)= \sum_i \dfrac{kq_i}{|\vec{r}-\vec{r}_i|} \]從電位的微分得到電場
當我們要計算電位的時候我們已經習慣使用距離反比定律來計算空間中的電位,但是我們不要忘了電位的原始定義是在電荷所建立的電場中進行路徑積分而得到。因為點電荷的電場大小與距離的平方成反比,經過路徑積分之後得到電位與距離的一次方成反比,這是積分的結果。既然如此,已知電場可以得到電位,反過頭來,積分的逆運算是微分,如果已知空間中的電位分佈函數,我們也原則上可以利用微分得到相對應的電場向量。要得到這個結果我們必須使用向量場的微分,稱為梯度的運算。關於梯度算符的精確定義與應用,同學們會在二年級的應用數學中再詳細介紹,在這個單元的學習中我們只簡單的寫出梯度的運算公式: \[\vec{E}=-\nabla V(x,y,z)\] \[\nabla V(x,y,z)= \dfrac{\partial V}{\partial x} \hat{i} + \dfrac{\partial V}{\partial y} \hat{j} + \dfrac{\partial V}{\partial z} \hat{k}\] 其中\(\dfrac{\partial V}{\partial x}\)代表對電位函數\(V(x,y,z)\)進行\(x\)的偏微分,也就是對\(V(x,y,z)\)進行\(x\)的微分時,將函數中的\(y\)和\(z\)視為常數。例如:\[V(x,y,z)=x^2 + y^2 +z^2 \\ \dfrac{\partial V}{\partial x}=2x; \quad \dfrac{\partial V}{\partial y}=2y; \quad \dfrac{\partial V}{\partial z}=2z \]等電位面
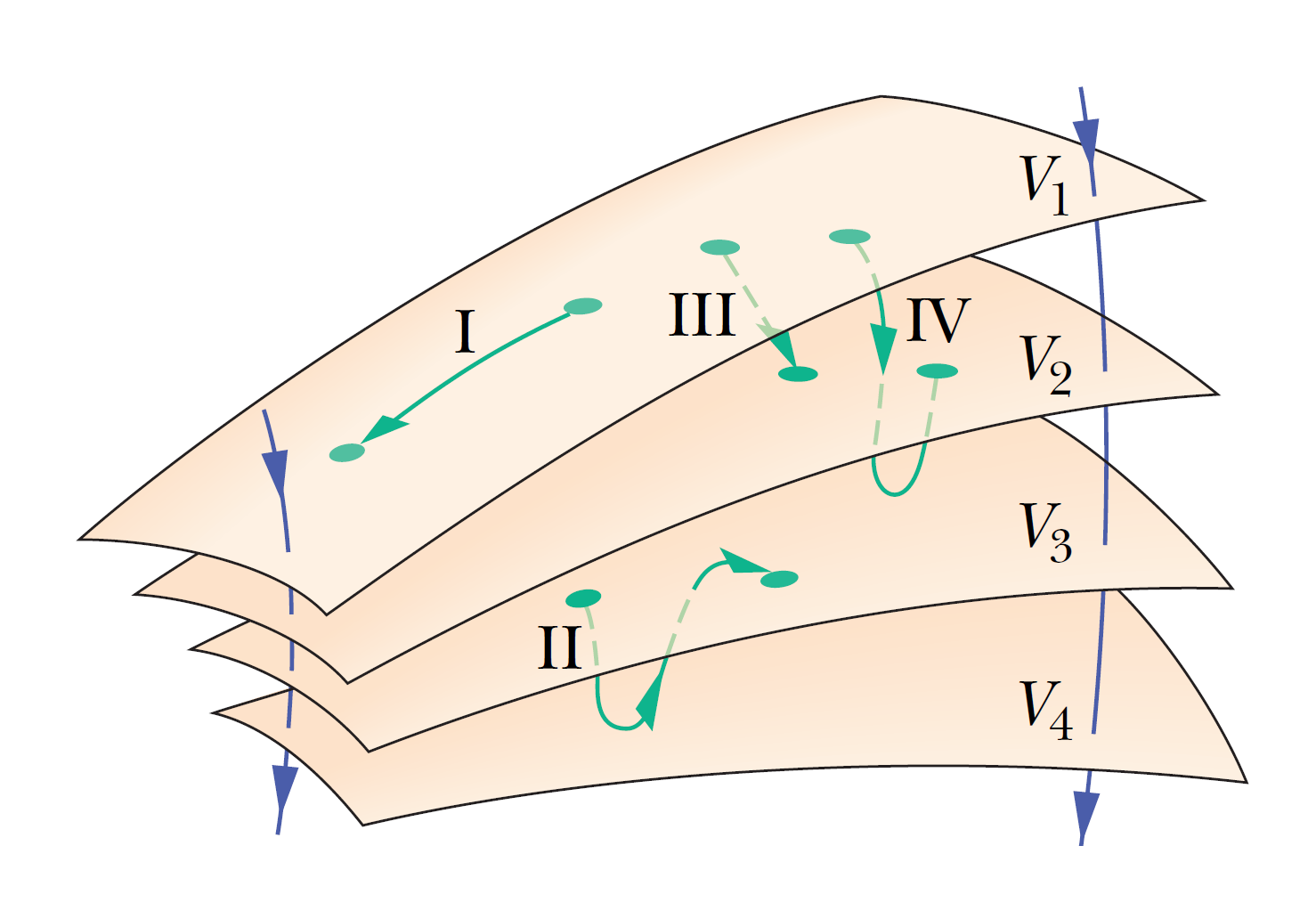 具有相同電位的相鄰點形成等位面,該等位面可能是想像的表面,也可能是真實的物理表面。當帶電粒子\(q_0\)在同一等位面上的兩點 \(i\) 和 \(f\) 之間移動時,電場不會對帶電粒子做淨功 \(W\), 因為 \(V_f= V_i,W=q_0 \Delta V=q_0 (V_f - V_i)=0\)。由於功的路徑獨立性,對於給定等位面上連接點 i 和 f 的任何路徑,無論該路徑是否完全位於該表面上,\(W= 0\)。
具有相同電位的相鄰點形成等位面,該等位面可能是想像的表面,也可能是真實的物理表面。當帶電粒子\(q_0\)在同一等位面上的兩點 \(i\) 和 \(f\) 之間移動時,電場不會對帶電粒子做淨功 \(W\), 因為 \(V_f= V_i,W=q_0 \Delta V=q_0 (V_f - V_i)=0\)。由於功的路徑獨立性,對於給定等位面上連接點 i 和 f 的任何路徑,無論該路徑是否完全位於該表面上,\(W= 0\)。在右圖中我們畫了4個等位面,並且選擇4個路徑。考慮路徑1和路徑2,當一個帶電粒子沿著路徑1移動時,帶電粒子始終是在一個等位面上移動,因此電位沒有改變,在路徑1的移動中在任何位置電力都不做功。考慮路徑2,雖然帶電粒子移動的過程跨越了不同的等位面,電位改變的過程中,電力做功,但是路徑2的終點回到起始點的等位面上,因此電力所作的淨功為0。第3個和第4個路徑都跨越了不同的等位面,並且起點和終點的電位不同,因此電荷沿著這兩個路徑移動,電力都必須做功。希望同學們能夠透過比較這4個路徑中電位的變化和電力做功的情況,進一步理解等位面的意義
從上面的討論中我們理解到,電荷的組態與電力解的幾何結構,乃至等位面的型態都是息息相關的,在下面的圖中我們呈現了幾種不同的電荷組態的電力線和等位面。
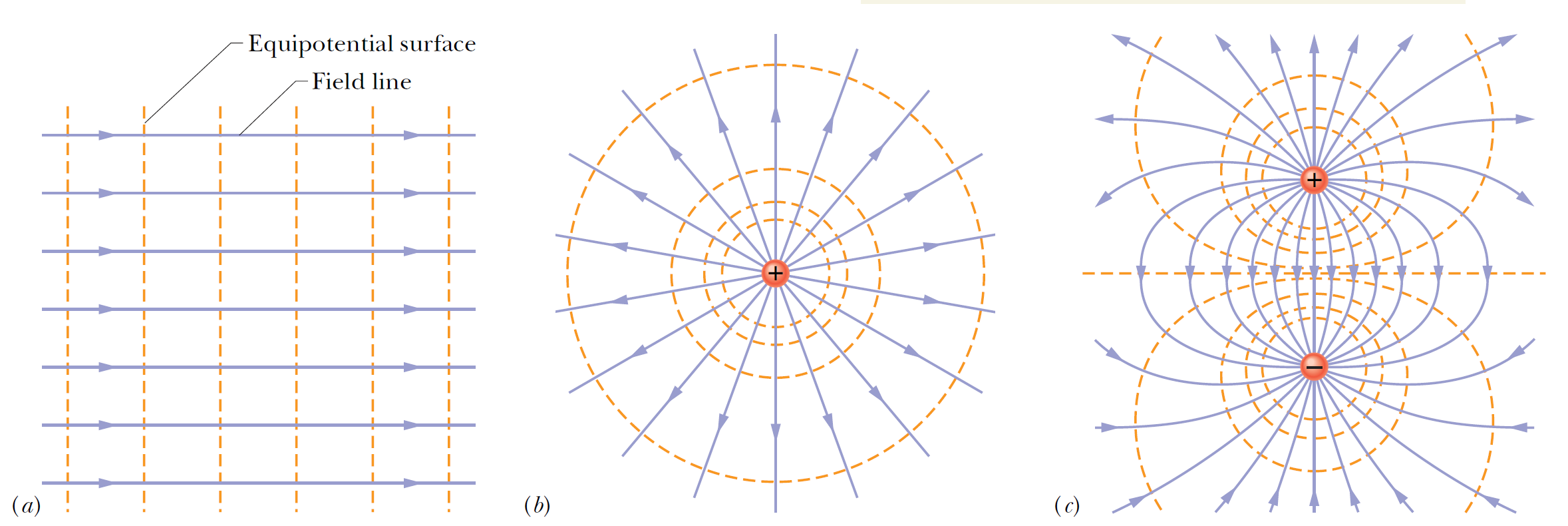
- 帶電平面的等位面 無論是第2單元應用庫倫定律直接計算電場,或是第3單元利用高斯定律來計算電場,我們已經知道帶電平面能夠提供一個方向與大小接均勻的電場\(E=\dfrac{\sigma}{2 \varepsilon_0}\),其電場的大小與面電荷密度\(\sigma \gt 0\)成正比,電場的方向在平面的法線方向上。根據我們上面關於電位的定義,我們選擇圖中沿著電力線向正x軸方向位移的直線路徑,路徑的切線方向就是面的法線方向,電場的方向與路徑的方向完全重疊,因此路徑積分當中的內積可以輕易算出,帶電平面的電位公式如下: \[ \Delta V =V_f - V_i = - \int_i^f \vec{E} \cdot d\vec{l} = -Ed =-\dfrac{\sigma d}{2 \varepsilon_0}\] 帶電平板的等位面顯然會是一個與電板平行的平面,在同一個平面上的電位都相等,電位隨著平面遠離帶電平板而逐漸下降\(\Delta V \propto -d\)。等位面始終與電場垂直。同樣的性質也應用在兩個帶異性電荷的平行電板的中間區域,這個討論我們會在下一個單元討論電容的時候會廣泛運用。
- 點電荷的等位面 點電荷的等位面點電荷的電場以電荷為中心,以球狀沿徑向向四面八方輻射,因此點電荷的等位面就是以電荷為球心的同心球面,在球面上的任何一點該處的電場與等位球面垂直。根據上面的推導我們知道,等位面的電位隨著遠離電荷而呈現1次方反比的關係,逐漸減小。
- 電偶極矩的等位面 我們考慮一正一負兩個電荷所形成的電偶極矩的等位面,當非常靠近其中一個電荷的時候,所有電場和電位的性質都由這個電荷主導,因此在正電荷附近的電場與單一點電荷的電場相近,所以等位面會以正電荷的位置為球心,形成同心球面的等位面。離開正電荷之後等位面就開始變大而且變形,直到到達兩個電荷的中點處,等位面會變成一個平面,兩個電荷連線的垂直平分面。越過中點之後,電場和電位的性質又漸漸地由負電荷主導,非常接近負電荷的時候又會形成以負電荷為球心的等位球面,這就是電偶極矩的等位面幾何結構。
靜電能
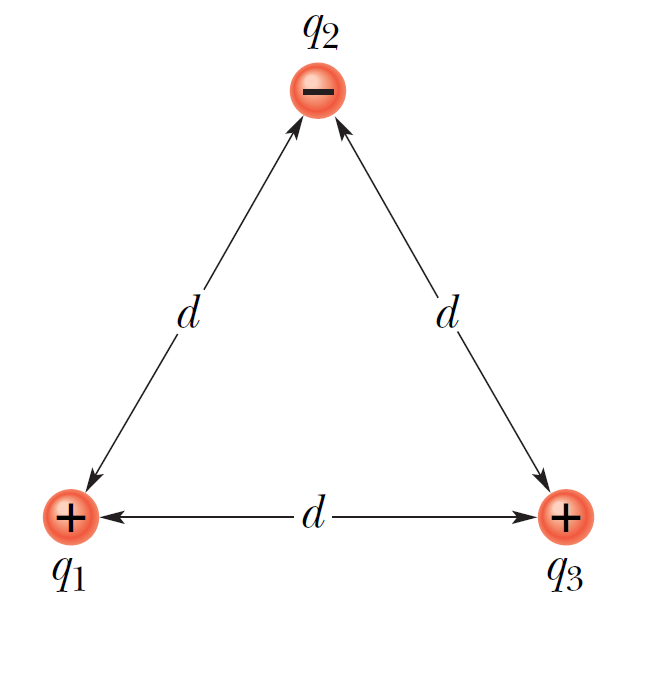
下面我們來考慮兩個關於靜電能的應用。- 假設我們有三個電荷分別從無窮遠處移動到圖中正三角形的三個頂點,請問這個過程中我們對系統做得多少功?有多少靜電位能儲存在這個電荷系統當中?
- 拉塞福散射實驗
 回答這個問題非常簡單,就是我們在討論靜電位能的時候已經了解點電荷之間的靜電位能與兩者距離的1次方成正比,
\[U_{12}=\dfrac{k q_1 q_2}{r_{12}}\]
並且利用線性疊加原理,我們可以把兩兩一對的電荷之間的靜電位能分別算出之後再加總,就可以得到系統中所儲存的總電位能,也就是外界對這個電荷系統所做的功。所以我們用下面的公式來回答整個問題:
\[U=U_{}+U_{}+U_{31}=\dfrac{k q_1 q_2}{r_{12}}+\dfrac{k q_2 q_3}{r_{23}}+\dfrac{k q_3 q_1}{r_{31}}=\dfrac{k}{d}[q_1 q_2+q_2 q_3+q_3 q_1] \]
回答這個問題非常簡單,就是我們在討論靜電位能的時候已經了解點電荷之間的靜電位能與兩者距離的1次方成正比,
\[U_{12}=\dfrac{k q_1 q_2}{r_{12}}\]
並且利用線性疊加原理,我們可以把兩兩一對的電荷之間的靜電位能分別算出之後再加總,就可以得到系統中所儲存的總電位能,也就是外界對這個電荷系統所做的功。所以我們用下面的公式來回答整個問題:
\[U=U_{}+U_{}+U_{31}=\dfrac{k q_1 q_2}{r_{12}}+\dfrac{k q_2 q_3}{r_{23}}+\dfrac{k q_3 q_1}{r_{31}}=\dfrac{k}{d}[q_1 q_2+q_2 q_3+q_3 q_1] \]
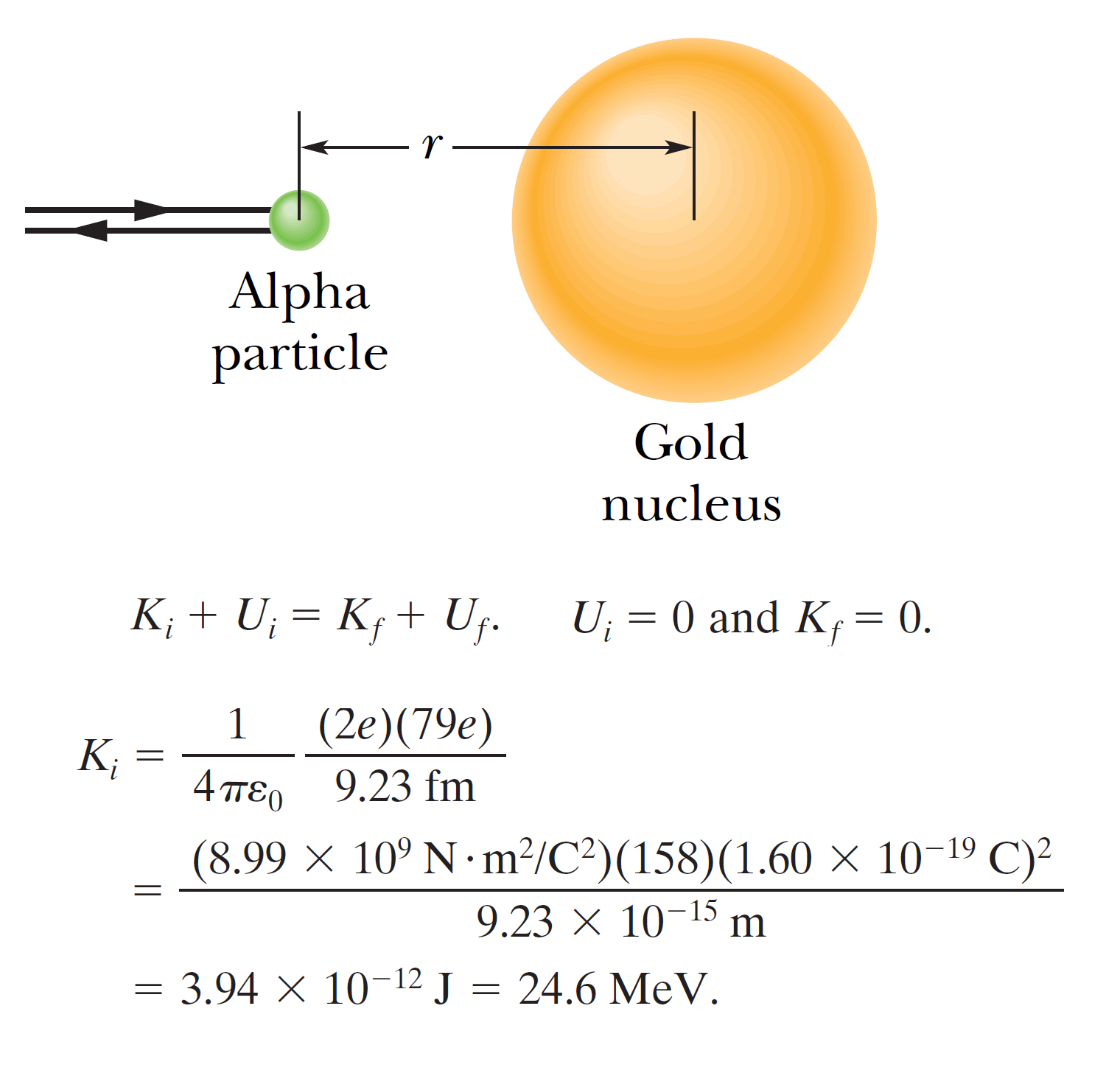 二十世紀初著名的拉塞福散射實驗的結果,讓拉塞福發現原子具有質量集中又帶正電的原子核。在散射實驗中拉塞福用\(\alpha\)粒子(阿法粒子)(帶正電,有兩個質子,兩個中子)來撞擊金原子。金原子基本上是由帶正電的原子核(79 個質子,118 個中子)吸引外圍的79個電子。入射的\(\alpha\)粒子因為質量遠遠大於電子,只要\(\alpha\)粒子的動能足夠大,就可以穿過電子殼層,向金原子核逼近。 \(\alpha\)粒子受到金原子核正電的排斥而開始減速,然後會在距離原子核\(r = 9.23 \times 10^{-15}\) m 時暫時停止,然後沿著入射路徑向後移動。我們的問題是要計算\(\alpha\)粒子的初始動能應該是多少?假設在整個過程中\(\alpha\)粒子和金原子核之間的庫倫排斥力,是\(\alpha\)粒子運動中唯一受到的力。
二十世紀初著名的拉塞福散射實驗的結果,讓拉塞福發現原子具有質量集中又帶正電的原子核。在散射實驗中拉塞福用\(\alpha\)粒子(阿法粒子)(帶正電,有兩個質子,兩個中子)來撞擊金原子。金原子基本上是由帶正電的原子核(79 個質子,118 個中子)吸引外圍的79個電子。入射的\(\alpha\)粒子因為質量遠遠大於電子,只要\(\alpha\)粒子的動能足夠大,就可以穿過電子殼層,向金原子核逼近。 \(\alpha\)粒子受到金原子核正電的排斥而開始減速,然後會在距離原子核\(r = 9.23 \times 10^{-15}\) m 時暫時停止,然後沿著入射路徑向後移動。我們的問題是要計算\(\alpha\)粒子的初始動能應該是多少?假設在整個過程中\(\alpha\)粒子和金原子核之間的庫倫排斥力,是\(\alpha\)粒子運動中唯一受到的力。計算的原則非常簡單,因為靜電力是一個保守力,保守力要滿足力學能守恆的條件,所以散射之初的力學能要等於阿法粒子停止時的力學能。在初始位置因為距離近原子核很遠,所以我們可以視為無窮遠處,電位能為零,所以力學能只有動能。在停止處動能為0,而電位能由距離反比定律決定,因此我們可以很快的計算出出時的動能就是靜止時的位能: \[ \dfrac{k q_{\alpha} q_{Au}}{r}=3.94 \times 10^{-12} \, \text{J} \] 焦耳(J)是能量和功的SI單位,但是在微觀世界當中,我們會習慣使用另外一個能量的單位,稱為電子伏特(electron volt, eV),也就是1個電子在1伏特的電位差作用下動能會增加一個電子伏特。 \[1 \, \text{eV} = \Delta U=q \Delta V=(1.6 \times 10^{-19} \, \text{C}) \cdot (1 \, \text{V})=1.6 \times 10^{-19} \, \text{J} \] 1個電子伏特等於\(1.6 \times 10^{-19}\)焦耳。電子伏特是一個非常重要的能量單位,在微觀世界、近代物理、量子物理、半導體工業與光電工業當中被廣泛應用,同學們一定要非常清楚這個能量單位與焦耳之間的換算關係。1 MeV=\(10^6\) eV。
導體的電場與電位
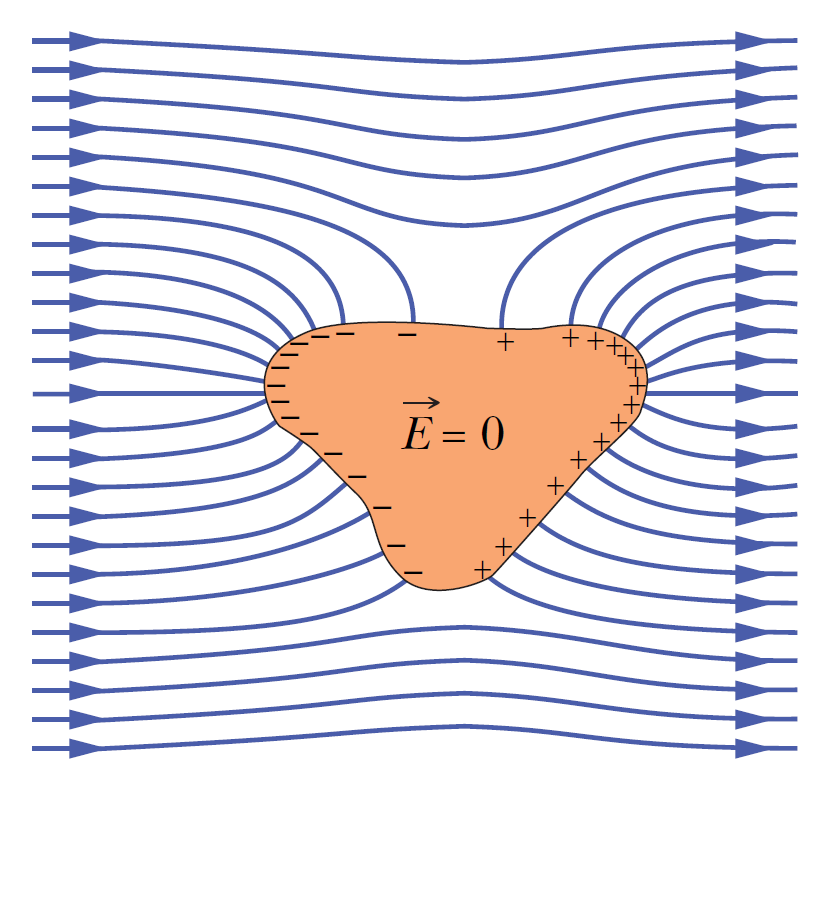 在第三單元,我們討論導體內部的電場,結論是導體的內部電場為零。因為電場如果不為零,就會讓導體內的導電電子在導體內部流動,如果電子會流動就不是一個平衡狀態,直到所有導電電子都不運動的時候,系統達到平衡必然會得到導體內部電場為零的結論。利用高斯定律我們知道,在導體內部選擇任何一個高斯面,高斯面上的電場都是0,根據高斯定律高斯面內的淨電荷為0。如果導體內部沒有空腔,或者有空腔但空腔內部沒有淨電荷,那麼導體的內部就不會有任何多餘的電荷,這是導體的基本性質。導體的電位性質又是如何呢?
在第三單元,我們討論導體內部的電場,結論是導體的內部電場為零。因為電場如果不為零,就會讓導體內的導電電子在導體內部流動,如果電子會流動就不是一個平衡狀態,直到所有導電電子都不運動的時候,系統達到平衡必然會得到導體內部電場為零的結論。利用高斯定律我們知道,在導體內部選擇任何一個高斯面,高斯面上的電場都是0,根據高斯定律高斯面內的淨電荷為0。如果導體內部沒有空腔,或者有空腔但空腔內部沒有淨電荷,那麼導體的內部就不會有任何多餘的電荷,這是導體的基本性質。導體的電位性質又是如何呢?因為導體內部的電場為零,所以根據電位差的定義,我們得到導體內部由導體所連通的路徑上電位差是0,也就是電位相等: \[E=0 \, \text{(inside conductor)} \Rightarrow \Delta V = \int_i^f \vec{E} \cdot \text{d}\vec{l}=0 \] 放置在隔離導體上的多餘電荷將自行分佈在該導體的表面上,因此導體的所有點(無論是在表面還是內部)都具有相同的電位。即使導體具有內部空腔和即使該空腔包含淨電荷,導體本身的所有點都具有相同的電位。一個不帶電的導體懸浮在外電場中。導體中的自由電子如圖所示分佈在表面上,從而使導體內部的淨電場降為零,使表面處的淨電場垂直於表面。
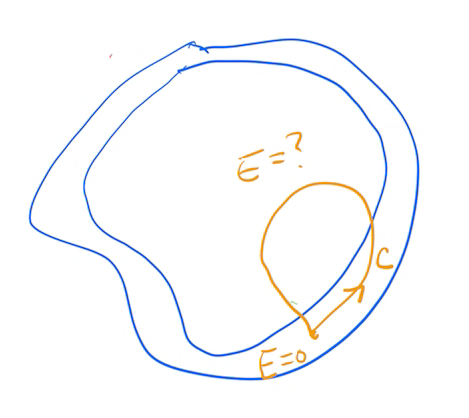 如果把這個導體變成是一個金屬導體殼,也就是內部是一個很大的空穴。同樣的感應電荷會重新分布,使得空穴的內部沒有電場存在。證明這個結果的方法很簡單,在左圖中我們選擇一個封閉的路徑,因為電場是保守場所以電場沿著這個路徑積分是0。這個路徑可以分成兩個部分,一個部分在導體本身的內部,另外一部分是在空穴當中,在導體之中的電場為0,因此在導體中的路徑積分貢獻是0。因為整個封閉路徑的積分為0,空穴中的路徑的積分也必須是0。因為這個路徑是隨意選取的,我們可以從導體的表面慢慢的向空穴的內部增加路徑的長度,所以電場為0的這個特性可以從導體的內部到導體的表面,一直延伸到空穴的內部,所以我們可以證明空穴的內部電場也是0。這是一個非常有趣的結果,他告訴我們,如果我們希望有一個空間能夠保持不被外部的電場侵入,我們只要用金屬的薄膜包住這個空間的外圍,就可使這個空間維持電場為零,不受外界電場的影響,這一個效應稱為導體的遮蔽效應(screening effect)。
如果把這個導體變成是一個金屬導體殼,也就是內部是一個很大的空穴。同樣的感應電荷會重新分布,使得空穴的內部沒有電場存在。證明這個結果的方法很簡單,在左圖中我們選擇一個封閉的路徑,因為電場是保守場所以電場沿著這個路徑積分是0。這個路徑可以分成兩個部分,一個部分在導體本身的內部,另外一部分是在空穴當中,在導體之中的電場為0,因此在導體中的路徑積分貢獻是0。因為整個封閉路徑的積分為0,空穴中的路徑的積分也必須是0。因為這個路徑是隨意選取的,我們可以從導體的表面慢慢的向空穴的內部增加路徑的長度,所以電場為0的這個特性可以從導體的內部到導體的表面,一直延伸到空穴的內部,所以我們可以證明空穴的內部電場也是0。這是一個非常有趣的結果,他告訴我們,如果我們希望有一個空間能夠保持不被外部的電場侵入,我們只要用金屬的薄膜包住這個空間的外圍,就可使這個空間維持電場為零,不受外界電場的影響,這一個效應稱為導體的遮蔽效應(screening effect)。
範例-1:地球表面附近的電勢能
|
來自太空的宇宙射線粒子不斷地將電子從大氣中的空氣分子中撞出,一旦被釋放,由於地球上已經存在的帶電粒子在大氣中產生的電場,每個電子都會受到靜電力的影響。在地球表面附近,電場的大小為 E=150 N/C,並且指向下方。當靜電力使其垂直向上移動時,當電子在鉛垂方向位移 520公尺,電子的電位能的變化 \(\Delta U\) 是多少? |

|
範例-2:電位差的計算(路徑積分)
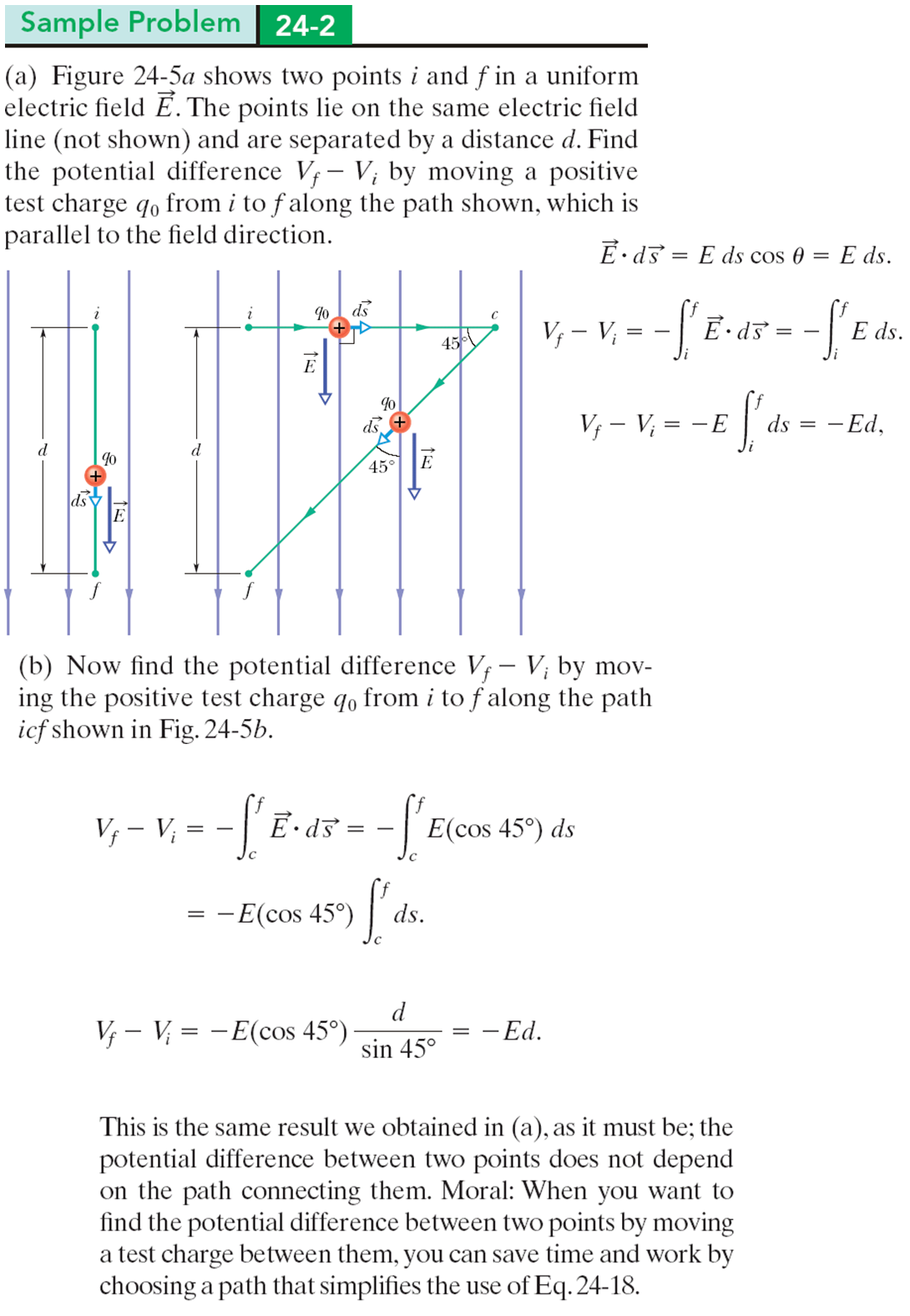
| (a) 圖中顯示了均勻電場中的兩點 \(i\) 和 \(f\)。這兩個點位於同一電場線上,並且相距 \(d\)。 通過沿所示路徑將正測試電荷 \(q_0\),沿著與場方向平行的路徑,從\(i\)移動到\(f\),請計算電位差 \(V_f - V_i\)。 (b)現在通過沿圖中所示的路徑\(icf\),將正測試電荷 \(q_0\) 從 \(i\) 移動到 \(f\),請計算電位差 \(V_f - V_i\)。 |
|
範例-3:電位差的計算(點電荷)
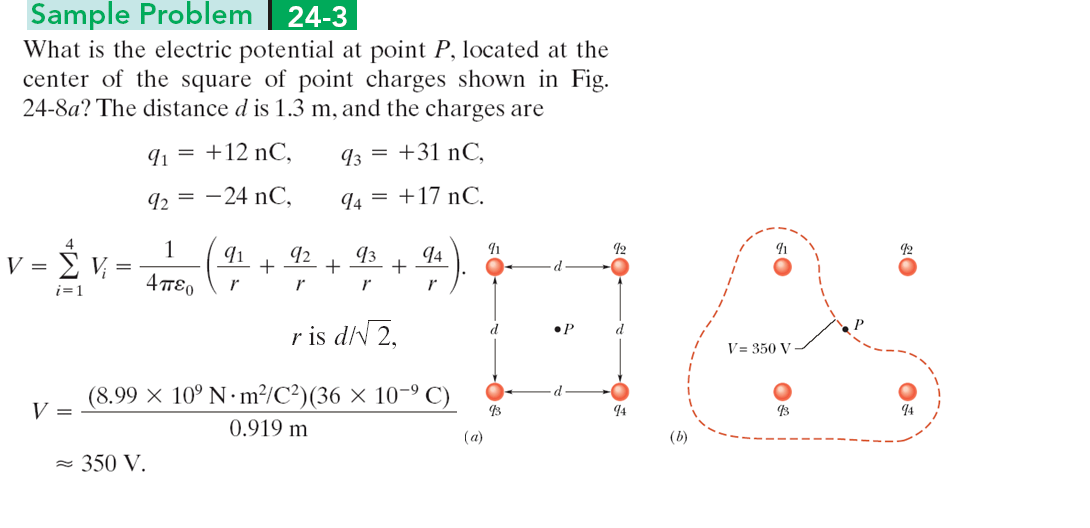
| 點 P 位於圖中點電荷正方形的中心,請計算其電位是多少? |
|
範例-4:帶電圓弧電位差的計算
|
(a)右圖中,12個電子(電荷=-e)等間距固定在一個半徑為\(R\)的圓上。相對於無窮遠處\(V=0\),由於這些電子而導致圓的中心\(C\)處的電位和電場是多少? (b)如果電子沿著圓移動直到它們在 120° 弧上不均勻地間隔(如圖),那麼 \(C\) 處的電位是多少? \(C\) 處的電場如何變化? |

|
範例-5:電位差的計算
|
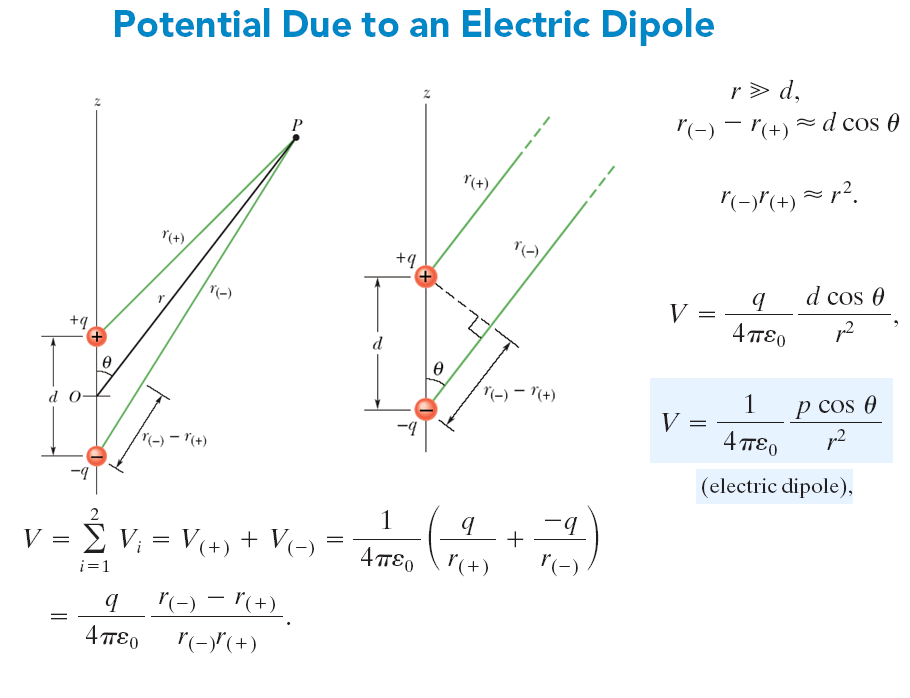
現在讓我們將點電荷的電位公式應用於電偶極子,以求出圖中任意點 \(P\) 的電位。 在 \(P\) 處,正點電荷(在距離 \(r_{(+)}\) 處)建立電位 \(V_{(+)}\),負點電荷(在距離 \(r_{(-)}\) 處建立電位 \(V_{(-)}\)。 \(P\) 處的淨電位根據線性疊加原理為兩者之和:
\[V_P=V_{(+)}+V_{()} \]
|
|
範例-6:均勻的帶電直線所貢獻的電位計算
|
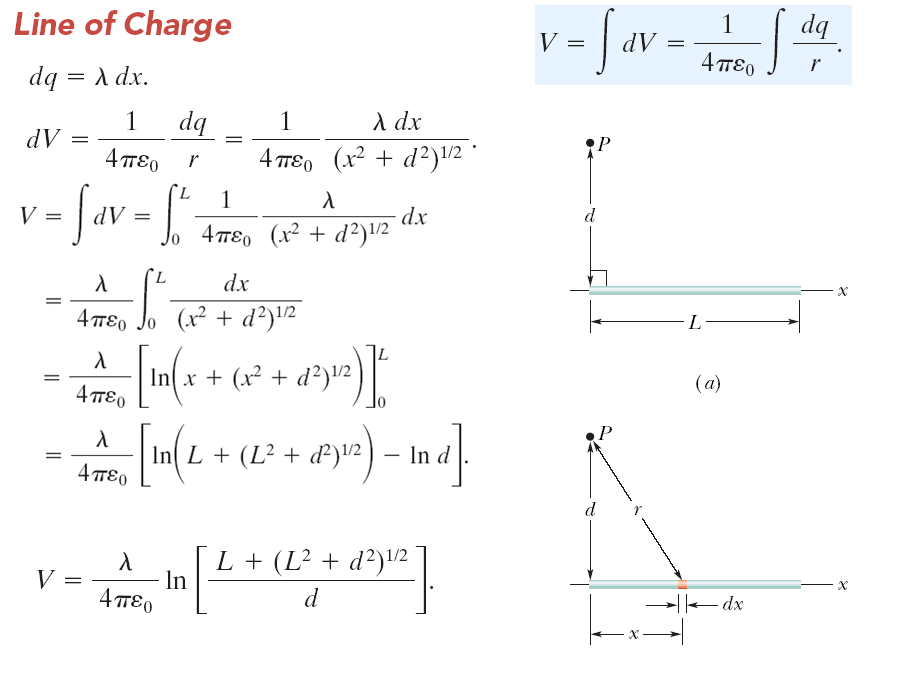
在圖中,長度為 \(L\) 的細不導電棒具有均勻線密度 \(\lambda\) 的正電荷。\(P\)點與棒的左端垂直距離 \(d\),請計算棒子上所帶的電荷在p點所建立的電位。 如圖所示,我們考慮桿的微分元素 \(dx\)。棒的這個(或任何其他)元素具有微量電荷 \(dq = \lambda dx\),該微量電荷在點 \(P\) 處產生電位 \(dV\)。點\(P\)與微量電荷的距離為 \(r = (x^2 + d^2)^{1/2}\)。將微量電荷視為點電荷,我們可以將電位 \(dV\) 寫為 \[ dV= \dfrac{1}{4 \pi \varepsilon_0} \dfrac{dq}{r} = \dfrac{\lambda dx}{ (x^2 + d^2)^{1/2}} \] 由於棒上的電荷是正的,並且我們在無窮遠處取 \(V = 0\),我們知道 \(dV\) 一定是正的。積分可能難以推導。但是您可以通過微分來驗證結果: \[ \dfrac{d}{dx} \ln \left( x+(x^2+d^2)^{1/2} \right) = \dfrac{1}{(x^2+d^2) ^{1/2}} \] |
|
範例-7:帶電塑膠圓盤中心軸上電位差的計算
|
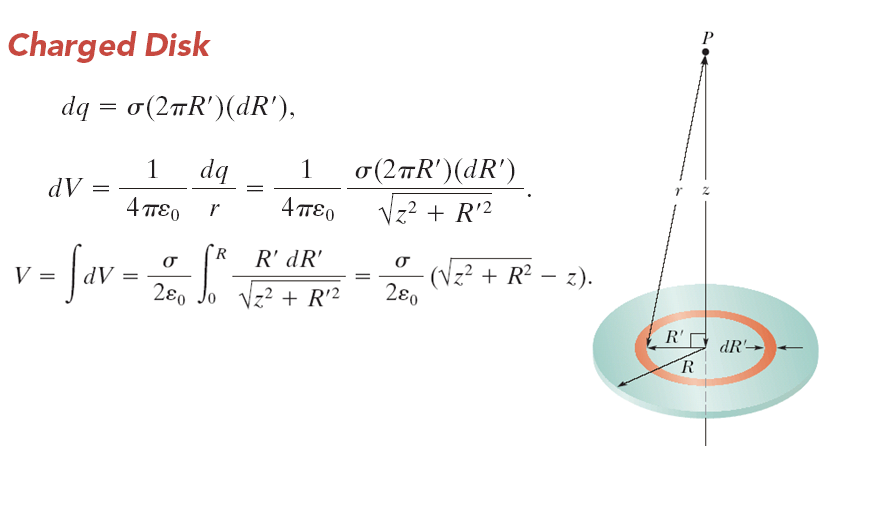
之前在第二和第三單元的時候,我們計算了半徑為 \(R\) 的帶電塑膠圓盤中心軸上各點的電場大小,該圓盤在一個表面上具有均勻的電荷密度 \(\sigma\)。 在此,我們推導出 \(V(z)\) 的表達式,即中心軸上任意點的電位。在圖中,考慮一個由半徑為 \(R'\) 和徑向寬度為 \(dR'\) 的圓環組成的微分元素。它的電荷量為 \(dq=\sigma (2 \pi R')(dR')\),其中 \(2 \pi R )(dR) \)是環的表面積。這個帶電元素的所有部分與圓盤軸上的點 \(P\) 的距離 \(r\) 相同。 從圖中我們不難發現,可以使用點電荷的電位公式將這個環對 \(P\) 處的電位的貢獻寫為
\[dV=\dfrac{1}{4 \pi \varepsilon_0} \dfrac{dq}{r}=\dfrac{1}{4 \pi \varepsilon_0} \dfrac{\sigma (2 \pi R')( dR')}{\sqrt{z^2+R'^2}} \]
同樣,您可以通過反向微分驗證積分結果。有了電位差的函數,我們可以透過微分得到電場的函數。
|
|
範例-8:電位函數的微分得到電場的函數
|
均勻帶電圓盤中心軸上任一點的電位由下式給出
\[V=\dfrac{\sigma}{2 \varepsilon_0} (\sqrt{z^2 + R^2} -z) \]
從這個表達式,導出圓盤軸上任意點的電場的公式。
|

|
範例-9:電荷系統的電位能
|
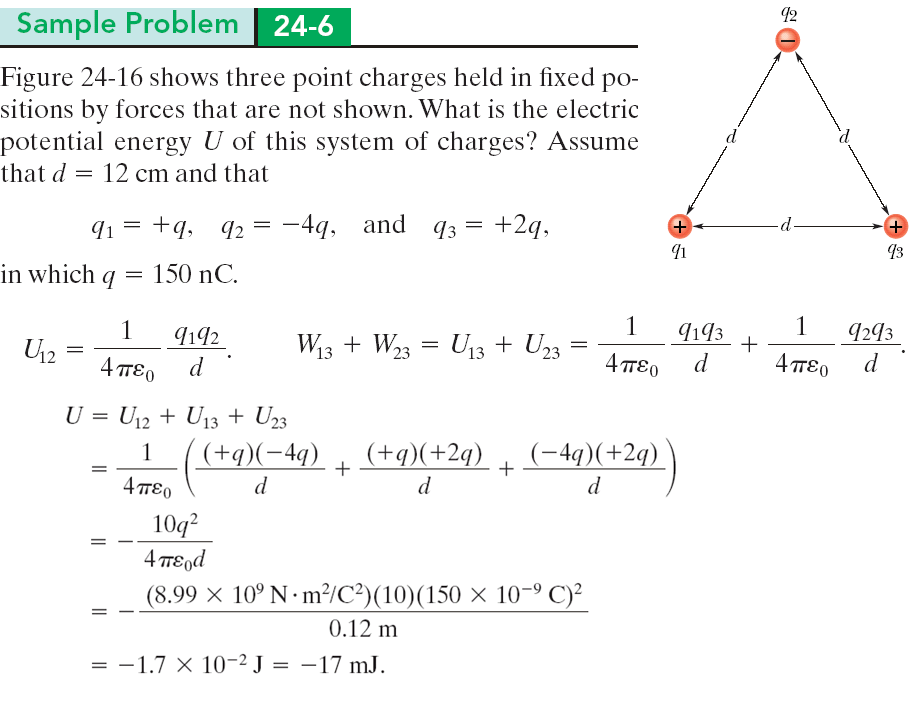
圖中顯示了三個點電荷通過未顯示的力保持在固定位置。 這個電荷系統的電位能 \(U\) 是多少? 假設 \(d = 12\) cm 並且
\[q1=+q, \quad q_2=-4q, \quad \text{and} \quad q_3 =+2q,\]
其中 \(q = 150\) nC。
|
|
授課教師
陳永忠 ycchen@thu.edu.tw