�q�e
���u�{�v�b�]�p�@�ǹ�Ϊ��]�ƮɡA�ݭn�@�ǰ��ѨӤF�ѳo�dz]�p�]�Ʈɩһݭn����z�A���z�Ǯa�N�b��¦��ǤW���u�{�v���ѳo�˪����ѡA�ڭ̦b�o�ӳ椸���n���Q���@�ӷ����`�����Ҥl�N�O�q�e���C�q�e���O�@�إi�H�x�s�q��˸m�A�Ҧp�b�Ӭ۾����A�q���q�L��q�e�����R�q�N��q�x�s�b�{���O�椸���C�q�����M������ѯ�q����t�v�O����w�C���A���{���O�Ө��q�����ѯ�q���t�v�����H���{���O�b�����o���A�۹�a�A�q�e���N�i�H�F��o�˪��\��C�q�e���@���Q�R�q�A���{���O�QIJ�o�ɥ��i�H�Χ��t�v�A���ѵ��{���O��q�A���{���O����o�X�@�}���G�����F��Ӭ۪��ت��C�q�e������z�]�Q���s���L���]�ơA�ҦpIJ���ù��ACCD�Ӭ۾��A���b���骺�����������s�b�q�e����z�C��L�P�q�����������p�A�Ҧp��H�Ǯa�b��s�a�y���j��h�����q���ɱN�a�y�ݦ��O�@�ӥ��j���q�e���A�ӹq�e���q�L�{�q������q�y���j��P�a�y���������{�q�C�ڭ̰Q�q�e�����Ĥ@�B�O�T�w�@�ӹq�e���i�H�s�x�h�ֹq���A�o�ӼƭȺ٬��q�e�ȡC�������O�P�q�e���w�q
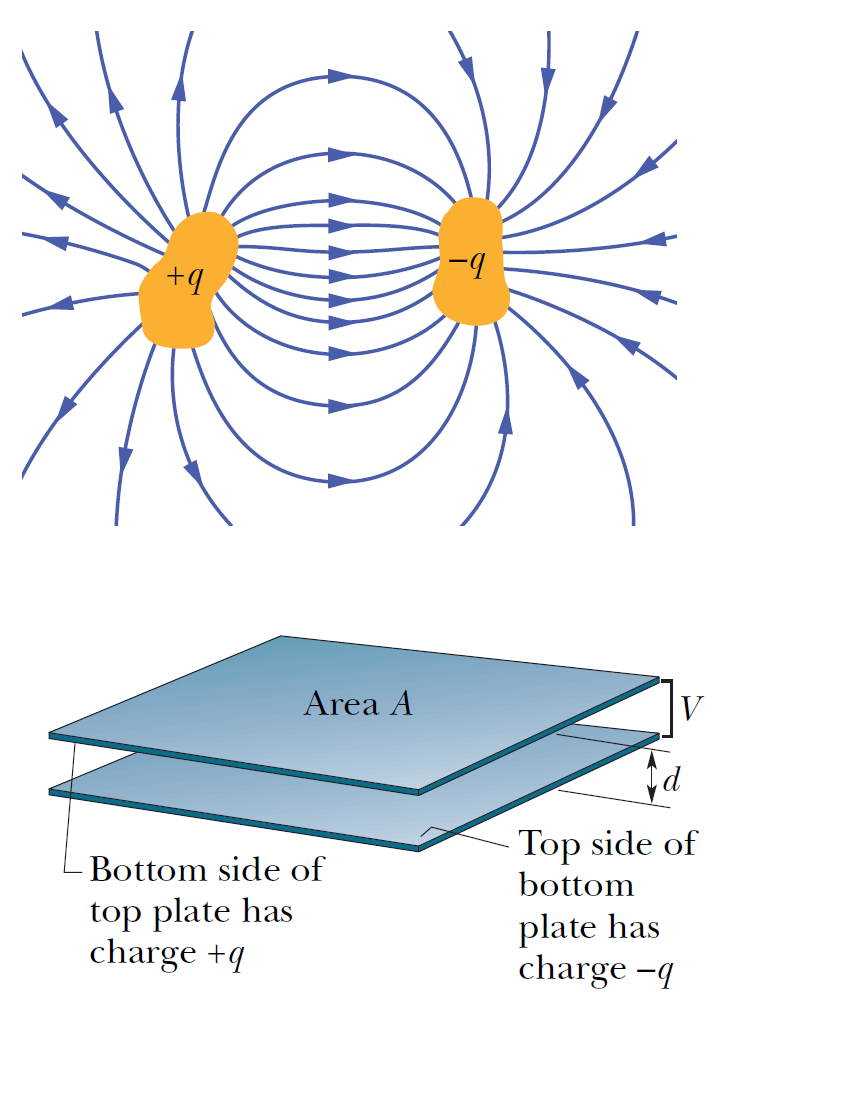 �k����ܤF�q�e�����զ��X�X����Ϊ�����ӹj������C�L�ץ��̪��X��Ϊ��p��A���Z�P�_�A�ڭ̳��ٳo�Ǿ���O�C��²�檺�q�e�N�O�������O�ҧΦ����q�e���A���]���歱�O�����n�OA�A��O�l�۹j���Z��d�C�p�G�ڭ̱q�W��������O���ʳ������q�l��m��U��������O�W�A�N�i�H�ϤW����O�a��\(+Q\)���q���A�U����O�a��\(Q\)���q���C�ڭ̫e�����椸���Q�L�a�q����O�����㦳���ê��q���A�q������V�q�a���q���W�q�O���V�a�t�q���U�q�O�A�q������V�¤U�P���O�����A�q�����j�p�P����O�����q���K��\(\sigma=Q/A\)�����C�P�˪��b��ӹq�O�����s�b�q��t\(\Delta V=Ed\)�G
\[\Delta V=Ed \\ =\dfrac{\sigma}{\varepsilon_0} d \\ =\dfrac{\sigma A}{\varepsilon_0 A} d \\ = \dfrac{Q d}{\varepsilon_0 A} \\ \Rightarrow Q \\ =\left[ \dfrac{\varepsilon_0 A}{d} \right] \Delta V \]
����O�W���a�q�qQ������ӥ���O�a�q��t�A�o�өʽ�i�H�s�x�a���Φb�Ҧ����q�e���W�C�]���@�ӹq�e������Ӿ���W���O�R�H���ʹq���A�]���|�y����Ӿ��餧���s�b�q���A�]�s�b�q��t�A���M�]�N�x�s���R�q���A�x�s�R�q���N�O�q�e�����D�n�\��C��e�@�ӹq�e���x�s�q������O�A�N�b�q���P�q��t��������ұ`�ơG
\[C=\dfrac{Q}{\Delta V} \quad \text{�b�S���V�c�����p�U�q��t��V�Ӫ��ܡG} C=\dfrac{Q}{V}\]
�k����ܤF�q�e�����զ��X�X����Ϊ�����ӹj������C�L�ץ��̪��X��Ϊ��p��A���Z�P�_�A�ڭ̳��ٳo�Ǿ���O�C��²�檺�q�e�N�O�������O�ҧΦ����q�e���A���]���歱�O�����n�OA�A��O�l�۹j���Z��d�C�p�G�ڭ̱q�W��������O���ʳ������q�l��m��U��������O�W�A�N�i�H�ϤW����O�a��\(+Q\)���q���A�U����O�a��\(Q\)���q���C�ڭ̫e�����椸���Q�L�a�q����O�����㦳���ê��q���A�q������V�q�a���q���W�q�O���V�a�t�q���U�q�O�A�q������V�¤U�P���O�����A�q�����j�p�P����O�����q���K��\(\sigma=Q/A\)�����C�P�˪��b��ӹq�O�����s�b�q��t\(\Delta V=Ed\)�G
\[\Delta V=Ed \\ =\dfrac{\sigma}{\varepsilon_0} d \\ =\dfrac{\sigma A}{\varepsilon_0 A} d \\ = \dfrac{Q d}{\varepsilon_0 A} \\ \Rightarrow Q \\ =\left[ \dfrac{\varepsilon_0 A}{d} \right] \Delta V \]
����O�W���a�q�qQ������ӥ���O�a�q��t�A�o�өʽ�i�H�s�x�a���Φb�Ҧ����q�e���W�C�]���@�ӹq�e������Ӿ���W���O�R�H���ʹq���A�]���|�y����Ӿ��餧���s�b�q���A�]�s�b�q��t�A���M�]�N�x�s���R�q���A�x�s�R�q���N�O�q�e�����D�n�\��C��e�@�ӹq�e���x�s�q������O�A�N�b�q���P�q��t��������ұ`�ơG
\[C=\dfrac{Q}{\Delta V} \quad \text{�b�S���V�c�����p�U�q��t��V�Ӫ��ܡG} C=\dfrac{Q}{V}\]
 �`��\(C\)�V�j�A���ܦb���w���q��t���U�A�i�H�x�s���q���N�V�h�A�x�s�q���O�N�V�j�C�ҥH�ڭ̧�o�@�Ӥ�ұ`�Ʃw�q���q�e�����q�e��(capacitance)�C�H�W�z������O�q�e�Ө��q�e��\(C=\dfrac{\varepsilon_0 A}{d}\)�A��P�������q�e���A�q�e�Ȫ������]���P�C�q�e���j�p�P�q�e���ؤo�B�X��Ϊ��M���Ʀ����A�ڭ̦b�U���|�v�@���СC�N����O�q�e���Ө��A�q�e�ȥ����O�����n�P����O�������Z�����Ϥ�C�ھڹq�e�Ȫ��w�q�ڭ̹q�e��SI���O�w�۰��H��S(C/V=F)�o�ӳ��ڭ̤S�٬��k��(F, Farad)�A���F�����k�ԲĦb�q�ϾǤW���^�m�A�q�e�����H�k�ԲĬ��W�C�Ъ`�N�b�ڭ̤�`�����Τ��k�ԬO�@�ӫD�`�j���q�e���A�q�`�ڭ̷|�ϥ�1 pF =10 -12F�����Ӵy�z�@��q�e�����q�e�ȡCpF=picofarad�F 1 \(\mu\)F=\(10^{-6}\) F=microfarad�C
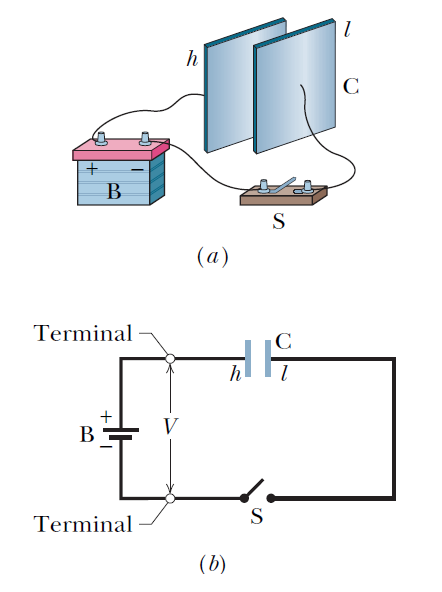
�`��\(C\)�V�j�A���ܦb���w���q��t���U�A�i�H�x�s���q���N�V�h�A�x�s�q���O�N�V�j�C�ҥH�ڭ̧�o�@�Ӥ�ұ`�Ʃw�q���q�e�����q�e��(capacitance)�C�H�W�z������O�q�e�Ө��q�e��\(C=\dfrac{\varepsilon_0 A}{d}\)�A��P�������q�e���A�q�e�Ȫ������]���P�C�q�e���j�p�P�q�e���ؤo�B�X��Ϊ��M���Ʀ����A�ڭ̦b�U���|�v�@���СC�N����O�q�e���Ө��A�q�e�ȥ����O�����n�P����O�������Z�����Ϥ�C�ھڹq�e�Ȫ��w�q�ڭ̹q�e��SI���O�w�۰��H��S(C/V=F)�o�ӳ��ڭ̤S�٬��k��(F, Farad)�A���F�����k�ԲĦb�q�ϾǤW���^�m�A�q�e�����H�k�ԲĬ��W�C�Ъ`�N�b�ڭ̤�`�����Τ��k�ԬO�@�ӫD�`�j���q�e���A�q�`�ڭ̷|�ϥ�1 pF =10 -12F�����Ӵy�z�@��q�e�����q�e�ȡCpF=picofarad�F 1 \(\mu\)F=\(10^{-6}\) F=microfarad�C�b�k�ϤW(a)�A�ڭ���ܤ@�Ӽзǹ�q�e�R�q����k�A�N�O�ϥΤ@�ӹq���M�@�Ӷ}���C���u�����n�F�H��A�N�}���s�q�q���N�|��q�e���}�l�R�q�A�q�e���W���q���|�q0�W�[�칡�M�q���C����Ӿ���㦳���M�q��\(+q, \, -q\)���ɭԡA��ӥ���O�������q��t�N�O�q����ݪ��q��t\(\Delta V= \mathscr{E}\)�A�䤤\(\mathscr{E}\)=�q�����q�ʶաC��ӽu�����˸m�i�H�e���k�ϤU(b)���q���ϡA�Ϥ��ڭ̥i�H�ݨ��Τ@�ӥ���O���Ÿ��ӥN���@�ӹq�e���C�b�ڭ̤U�����ҵ{���|�g�`�ݭn��q�e�B�q���B�q�������e�ϡA�b�o�عq���Ϥ��q�e���o�Ӥ���N�H�@�ӥ���O���Ÿ��N���o�Ӥ���m�M�q�e�Ȫ��j�p�C
�P�b��W��q�e
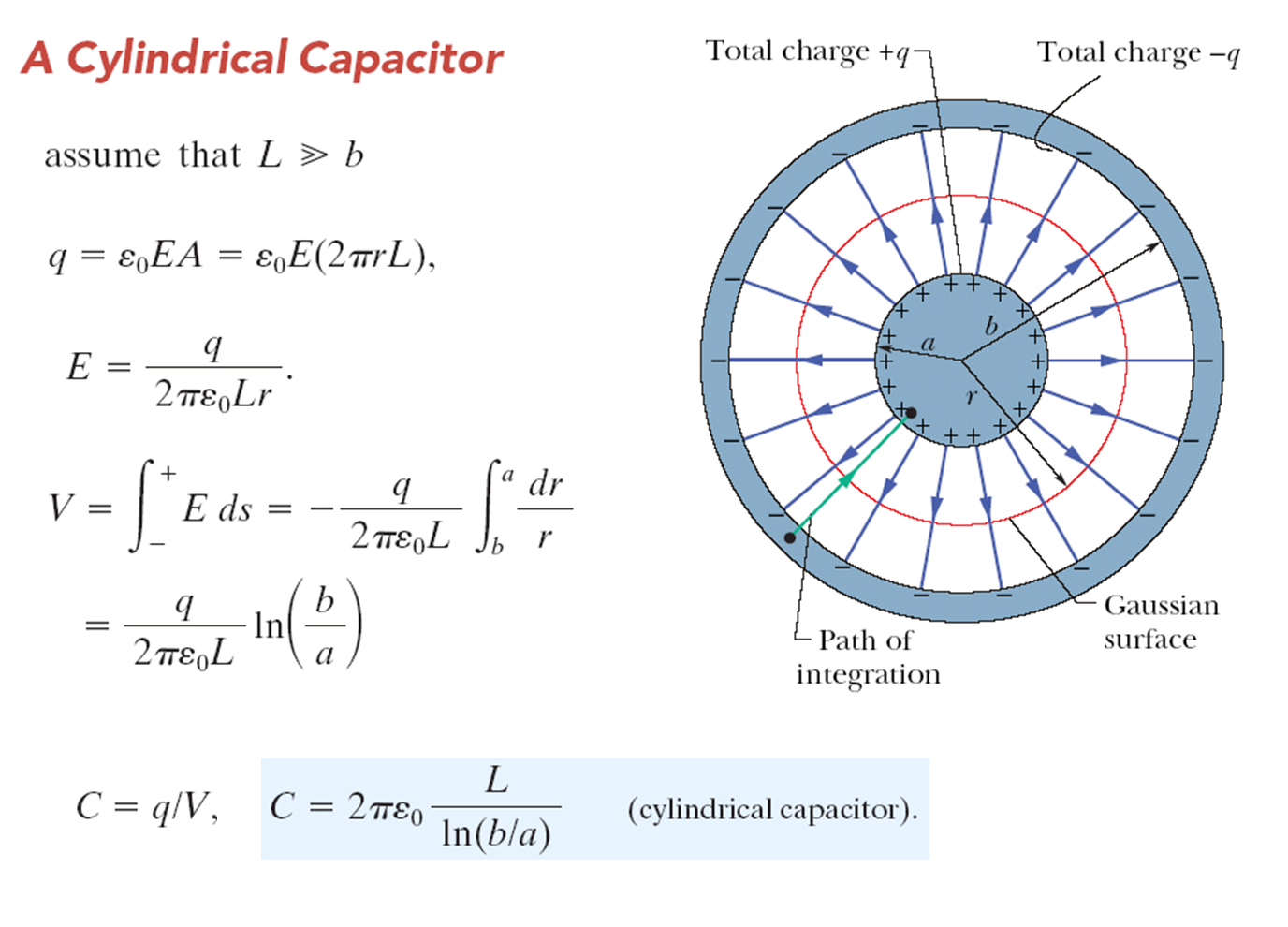
�@�Ӫ��� \(L\) ����W�ιq�e���A�Ѩ�ӥb�|�� \(a\) �M \(b\) ���P�b��W��զ��C �ڭ̰��] \(L \gg b\) �H�K�ڭ̥i�H������W�饽�ݲ��ͪ��q����t�~�X�C����W��a \(+q\) ���q���A�~��W��a \(-q\) ���q���C�F�n�p��o�ӹq�e���q�e�ȡA�ڭ̥����n��X�q��t�A�ӹq��t�O�q�������|�n���A�ҥH�����ڭ̭n�Q�ΰ����w�ߨӱ��ɹq���������C�q��W�骺�����Ϥ��ڭ̬ݨ��~�߾���M���h���餺�h���餧�����q������V�O�Ѷb�ߦV�~��g�P��W�������A�]���ڭ̿�ܤ@�Ӫ��� \(L\) �M�b�|�� r ���P�����W��@�b�ߪ���W���@�����������A�p�Ͼ�⪺��ҥܡC��W���������q�q�q�p��P�a�q���u���p�������A�b�W�\�M�U�\�������]���q���P�\�l�ꭱ���k�u��V�����A�]���W�U��ӻ\�l�S���q�q�q���^�m�C�����������k�u�M�q������A�]��������q�����W�������n�N�O���������q�q�q�C�]���ڭ̱o��P�b��W�骺�q�������P�a�q���u�������@�ˡG \[E=\dfrac{q}{2\pi \varepsilon_0 L r}\]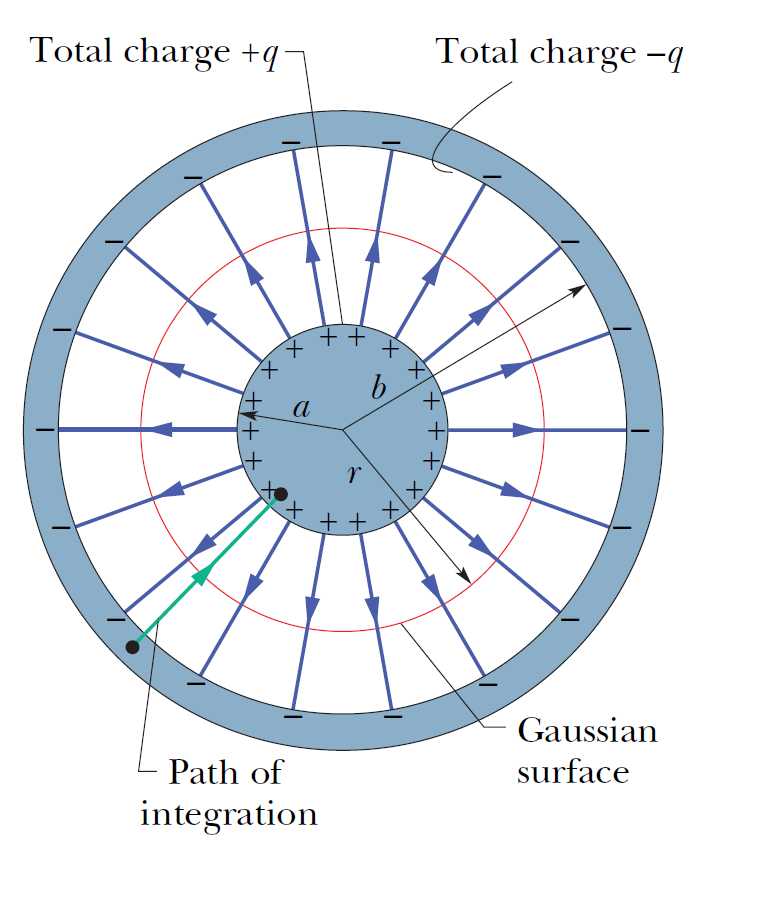 ��W�餺�����q�����j�p�]�O�P�Z�����@����Ϥ�A�b��q���u�ۥb�|�¥~����V�n���N�i�H�o���Ӿ��餧�����q��t�G
\[\Delta V = \dfrac{q}{2\pi \varepsilon_0 L} \ln \dfrac{b}{a} \]
�̫�ھڹq�e���w�q�N�a�q�q���H�q��t�A�o��q�e�������G
\[C=\dfrac{Q}{\Delta V}=2 \pi \varepsilon_0 \dfrac{L}{\ln (b/a)} .\]
��W�餺�����q�����j�p�]�O�P�Z�����@����Ϥ�A�b��q���u�ۥb�|�¥~����V�n���N�i�H�o���Ӿ��餧�����q��t�G
\[\Delta V = \dfrac{q}{2\pi \varepsilon_0 L} \ln \dfrac{b}{a} \]
�̫�ھڹq�e���w�q�N�a�q�q���H�q��t�A�o��q�e�������G
\[C=\dfrac{Q}{\Delta V}=2 \pi \varepsilon_0 \dfrac{L}{\ln (b/a)} .\]
�P�߾���y�q�e
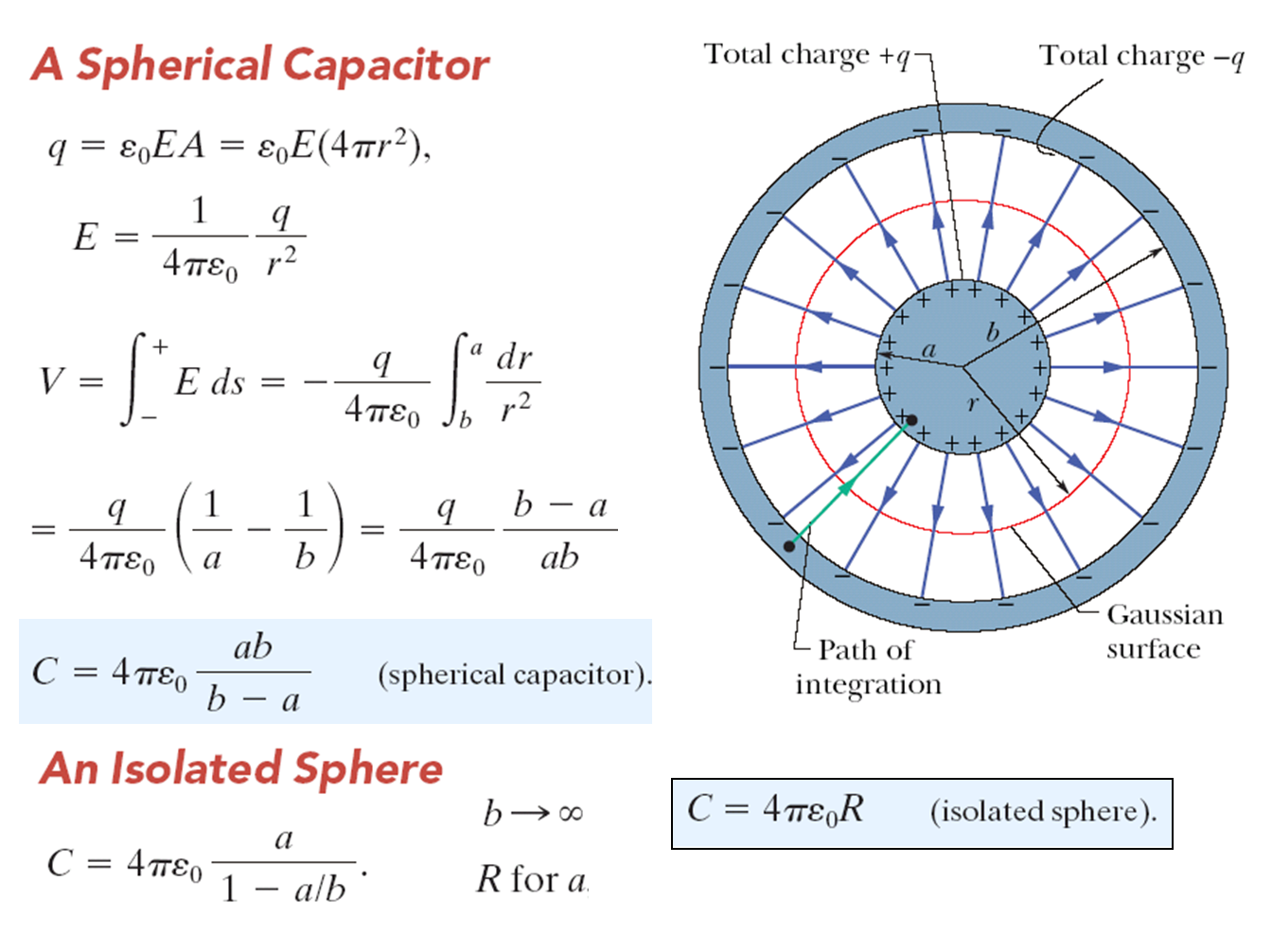
�W�Ϥ]�i������ӦP�ߪ�����y�A���y���b�|�O\(a\)�A�~�y���b�|�O\(b\), (\(b \gt a \))�A�ڭ̭n�p��o�ӦP�߾���y���q�e�C��h�W�q�e�����ӥu��o�ӹq�e�X�c���ѼƦ����A�P���~�y�ұa���q�q�L���A���O���F�p��X�q�e�ȡA�ڭ̰��]�b���y�a����q���`�q�q�A�~�y�a���tq���`�q�q�A�ڭ̧Q�ΰ����w�ߥi�H���p��X�b�����y�������q���j�p�C�z�L�q��t�һݭn���q�����|�n���A�i�H�p��X��y�������q��t�C�ڭ̪��D���y���q��@�w����~�y���q��A�p�⪺�����p�U�G \[ �����w�ߡG E(4 \pi r^2)=\dfrac{Q}{\varepsilon_0} \Rightarrow E=\dfrac{Q}{4 \pi \varepsilon_0 r^2} \] \[��y�������q��t�G \Delta V=\int_b^a \dfrac{Q}{4 \pi \varepsilon_0 r^2} dr= \dfrac{Q}{4 \pi \varepsilon_0}(1/a -1/b) \] �ھڹq�e���w�q�ڭ̥i�H�o��o�ӦP�߾���y���q�e���� \[C=\dfrac{Q}{\Delta V}=4 \pi \varepsilon_0 \left( \dfrac{ab}{b-a} \right) \] ���]�o�O��ӫD�`�j���P�߲y�A���~�|�������t���ܤp�G(\(b -a=d \ll a ) \)�A�W�z�������i�H����p�U�G \[C \approx \dfrac{\varepsilon_0(4 \pi a^2)}{d}=\dfrac{\varepsilon_0 A}{d} \] �o�ӵ��G���P��q�O���q�e�C��@����y���q�e
�p�G�ڭ̧�W�����Q�פ����~����y���b�|�ͪ��L�a�j(\(b \rightarrow \infty \) )�A�b�������Ŷ����N�u���@�ӳ�@�@�Ӿ���y�A�b�|��\(a\)�A�b�o�ӱ��p�U�q�e�������|�ܦ��G \[C=4 \pi \varepsilon_0 \left( \dfrac{ab}{b} \right)=4 \pi \varepsilon_0 a\] �o�Ӥ����N�O�@�Ӿ���y���q�e�ȡA�q�e�Ȫ��j�p�u�P�y���b�|�����A�P�y���b�|������A�y�V�j�q�e�ȴN�V�j�C�q�e���p�P���p
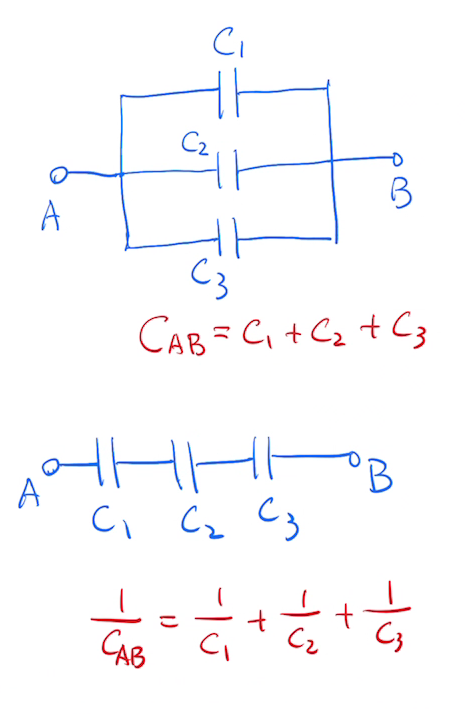 �ڭ̦b���ǮɥN���ǹL�q�y������������q�������p�M���p�A���D���˭p����p�q���M���p�q�������Ĺq���A�P�˪��A�X�ӹq�e�s���b�@�_�A�i�H�Ψ��p�M���p���զX�C�����ڭ̨ӦҼ{�q�e�����p�C�ڭ̨ӦҼ{3�ӥ���O���q�e���A�p�G�ڭ̧�T�ӹq�e���@�ݱ��b�q�������ݡA�T�ӹq�e���t�~�@�ݳ����b�q�����t�q�ݡA�p�ϩҥܡC�q���N�|��o3�ӹq�e�R�q�A�q�q���Ҭy�X���q���`�q����3�ӹq�e�W���q���Ȫ��`�M�A�åB�]���T�ӹq�e�O���p�A�]���T�ӹq�e���q��t���O�q����ݪ��q��t�C�ھڹq�e���w�q�ڭ̥i�H�g�U�U���T�ӻP�q�e��������{���G
\[Q_1=C_1 V; \quad Q_2=C_2 V; \quad Q_3=C_3 V; \quad \]
�N�o�T�ӹq���[�b�@�_�A�ڭ̥i�H�ܧ֪��ҩ��A���Ī��q�e�ȴN�O�T�ӹq�e���q�e�Ȫ��`�M�G
\[Q=Q_1+Q_2+Q_3=(C_1 + C_2 + C_3) V \]
\[\Rightarrow C_{eq}=C_1 + C_2 + C_3 \]
���סG�q�e���p�����Ĺq�e�ȬO�U���߹q�e���q�e�Ȥ��M�C����o�ӵ��קڭ̥i�H�q�U�����Q�רӲz�ѡC�ڭ�3�ӹq�e���T�ӥ���O�Һc�����q�e�A���ڭ̧�3�ӹq�e���@���s���b�@�_���ɭԵ��P��N�q�e�����n�W�j�A����O�������Z���S�����ܡA�]�����Ĺq�e����O�N���n�[���ӶZ�����ܪ��q�e�A�]���ھڥ���O�q�e�������G
\[C_{eq}=\dfrac{\varepsilon_0 (A_1 + A_2 + A_3)}{d}=\dfrac{\varepsilon_0 A_1}{d}+\dfrac{\varepsilon_0 A_2}{d}+\dfrac{\varepsilon_0 A_3}{d}=C_1 + C_2 + C_3 \]
���Ĺq�e�ȴN�H�ۭ��n�[�j���ܤj�C
�ڭ̦b���ǮɥN���ǹL�q�y������������q�������p�M���p�A���D���˭p����p�q���M���p�q�������Ĺq���A�P�˪��A�X�ӹq�e�s���b�@�_�A�i�H�Ψ��p�M���p���զX�C�����ڭ̨ӦҼ{�q�e�����p�C�ڭ̨ӦҼ{3�ӥ���O���q�e���A�p�G�ڭ̧�T�ӹq�e���@�ݱ��b�q�������ݡA�T�ӹq�e���t�~�@�ݳ����b�q�����t�q�ݡA�p�ϩҥܡC�q���N�|��o3�ӹq�e�R�q�A�q�q���Ҭy�X���q���`�q����3�ӹq�e�W���q���Ȫ��`�M�A�åB�]���T�ӹq�e�O���p�A�]���T�ӹq�e���q��t���O�q����ݪ��q��t�C�ھڹq�e���w�q�ڭ̥i�H�g�U�U���T�ӻP�q�e��������{���G
\[Q_1=C_1 V; \quad Q_2=C_2 V; \quad Q_3=C_3 V; \quad \]
�N�o�T�ӹq���[�b�@�_�A�ڭ̥i�H�ܧ֪��ҩ��A���Ī��q�e�ȴN�O�T�ӹq�e���q�e�Ȫ��`�M�G
\[Q=Q_1+Q_2+Q_3=(C_1 + C_2 + C_3) V \]
\[\Rightarrow C_{eq}=C_1 + C_2 + C_3 \]
���סG�q�e���p�����Ĺq�e�ȬO�U���߹q�e���q�e�Ȥ��M�C����o�ӵ��קڭ̥i�H�q�U�����Q�רӲz�ѡC�ڭ�3�ӹq�e���T�ӥ���O�Һc�����q�e�A���ڭ̧�3�ӹq�e���@���s���b�@�_���ɭԵ��P��N�q�e�����n�W�j�A����O�������Z���S�����ܡA�]�����Ĺq�e����O�N���n�[���ӶZ�����ܪ��q�e�A�]���ھڥ���O�q�e�������G
\[C_{eq}=\dfrac{\varepsilon_0 (A_1 + A_2 + A_3)}{d}=\dfrac{\varepsilon_0 A_1}{d}+\dfrac{\varepsilon_0 A_2}{d}+\dfrac{\varepsilon_0 A_3}{d}=C_1 + C_2 + C_3 \]
���Ĺq�e�ȴN�H�ۭ��n�[�j���ܤj�C�۹諸�p�G�ڭ̱N�T�ӹq�e���p�b�@�_�A�A�H�@�ӹq���ӥR�q���ɭԡA�L��3�ӹq�e�Ȫ��j�p�p��A�T�ӹq�e�W���q���������ۦP�A�]���ڭ̤]�|�o��U��3�ӵ����G \[V_1=\dfrac{Q}{C_1}; V_2=\dfrac{Q}{C_2}; V_3=\dfrac{Q}{C_3}\] �]���O���p�]���T�ӹq�e�U�۪��q��t�ۥ[����|����q�����q��t�G \[V=V_1 + V_2 + V_3=Q \left[\dfrac{1}{C_1}+\dfrac{1}{C_2}+\dfrac{1}{C_3} \right] \] �]���ڭ̥i�H�o����p�����Ĺq�e�ȡG \[\dfrac{V}{Q}=\dfrac{1}{C_{eq}}=\left[\dfrac{1}{C_1}+\dfrac{1}{C_2}+\dfrac{1}{C_3} \right] \] �T�ӹq�e���p�����Ĺq�e���q�e�ȻP�U���߹q�e���q�e�Ȥ��������Y�O�˼Ƭۥ[�����Y�A������q�������p�������p�ⵥ�Ĺq���p��C����o�ӵ��G�ڭ̤]�i�H�ܧ֪��b�w�ʤW�z�ѡC���ӹq�e�Τ@���q�u��q�e���p�۱����ɭԡA�o�s�����o�⭱�q�e�O���M�㦳���q�����ʹq���A�]���۷���N��ӹq�e��K�b�@�_�A��IJ�������驿�����p�A�N�o��@�ӹq�e�A�۷���N�O�l���Z���[�j�A�Ҽ{���T�Ӧ��p���q�e�h�Z���ܱo��j�A�]���q�e���p���ɭԵ��P��N����O�������Z����j�A�]�����Ĺq�e�|�U���C
�D�ѹq�e����
 �N���q�պ����@�˧ڭ̥i�H�Ҽ{�h�ӹq�e�M�h�ӹq���s�����@�Ӻ����A�q����q�e�R�q�ϱo�C�@�ӹq�e�W�����Y�z�q���A�ڭ̥i�H�Q�ιq�e���w�q�M�W���ҰQ������h�ӹq�e���p�P���p�����Ĺq�e�A�ӭp��C�@�ӹq�e�W���q���q�M�q��t�A�]�N�O�n�D�Ѥ@�ӹq�e�����C
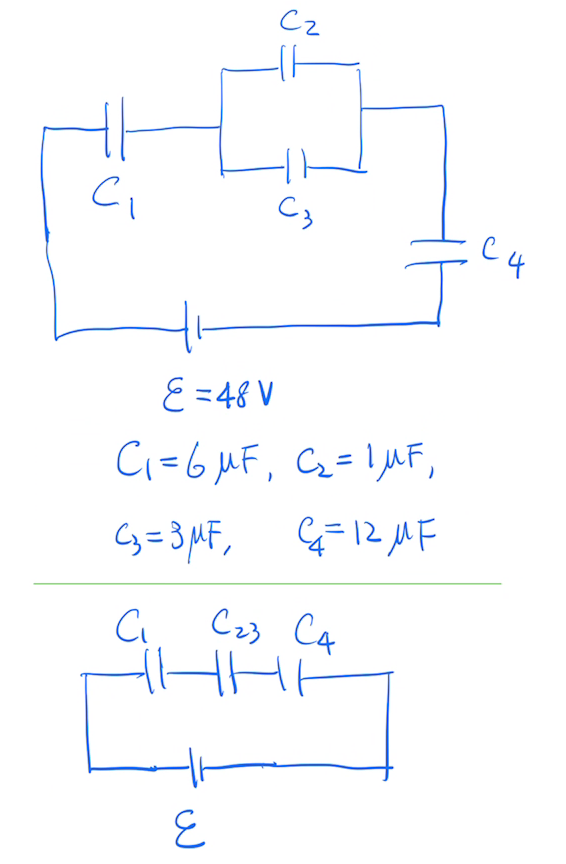
�b�k�Ϥ�
�@��48��S���q���s���F4�ӹq�e�A�ڭ̪��ت��O�n�p��X�A���t�ιF�쥭�Ū��ɭԡA�b4�ӹq�e�W���q���q�U���h�֡C�����ڭ̱q\(C_2, C_3\)�o��Ө��p�q�e�o��䵥�Ĺq�e�Ȭ���ӹq�e���M\(C_{23}=C_2+C_3=4\, \mu\)F�C���۴N�O\(C_1, C_{23}, C_4\)�T�ӹq�e�����p�A�i�H�o����骺���Ĺq�e�Ȭ�
\[C_{eq}=\dfrac{1}{1/6 + 1/4 + 1/12}=\dfrac{1}{6/12}=2 \,\mu \text{F}\]
�]���i�H�p��X�q�q���`�@��X�F�h�ֹq��\(Q\)
\[Q=C_{eq} V=2(48)=96 \,\mu \text{C}\]
\(C_1, C_4\)�P�q�����p�A�ҥH��ӹq�e�W���q���q�P�q����X���`�q�q�۵�:\(Q_1=Q_4=Q=96\,\mu \text{C}\)�C\(Q_2,Q_3\)���q���q�`�X�]�O\(Q\)�A�]����̨�ݹq���ۦP(\(Q_2/C_2=V_2 =V_3=Q_3/C_3\))�A�ҥH�q���q�P�q�e�Ȧ�����A�]���ڭ̥i�H�o��U�q�e�W���`�q�q���O�p�U�G
�N���q�պ����@�˧ڭ̥i�H�Ҽ{�h�ӹq�e�M�h�ӹq���s�����@�Ӻ����A�q����q�e�R�q�ϱo�C�@�ӹq�e�W�����Y�z�q���A�ڭ̥i�H�Q�ιq�e���w�q�M�W���ҰQ������h�ӹq�e���p�P���p�����Ĺq�e�A�ӭp��C�@�ӹq�e�W���q���q�M�q��t�A�]�N�O�n�D�Ѥ@�ӹq�e�����C
�b�k�Ϥ�
�@��48��S���q���s���F4�ӹq�e�A�ڭ̪��ت��O�n�p��X�A���t�ιF�쥭�Ū��ɭԡA�b4�ӹq�e�W���q���q�U���h�֡C�����ڭ̱q\(C_2, C_3\)�o��Ө��p�q�e�o��䵥�Ĺq�e�Ȭ���ӹq�e���M\(C_{23}=C_2+C_3=4\, \mu\)F�C���۴N�O\(C_1, C_{23}, C_4\)�T�ӹq�e�����p�A�i�H�o����骺���Ĺq�e�Ȭ�
\[C_{eq}=\dfrac{1}{1/6 + 1/4 + 1/12}=\dfrac{1}{6/12}=2 \,\mu \text{F}\]
�]���i�H�p��X�q�q���`�@��X�F�h�ֹq��\(Q\)
\[Q=C_{eq} V=2(48)=96 \,\mu \text{C}\]
\(C_1, C_4\)�P�q�����p�A�ҥH��ӹq�e�W���q���q�P�q����X���`�q�q�۵�:\(Q_1=Q_4=Q=96\,\mu \text{C}\)�C\(Q_2,Q_3\)���q���q�`�X�]�O\(Q\)�A�]����̨�ݹq���ۦP(\(Q_2/C_2=V_2 =V_3=Q_3/C_3\))�A�ҥH�q���q�P�q�e�Ȧ�����A�]���ڭ̥i�H�o��U�q�e�W���`�q�q���O�p�U�G
\[Q_1=96\,\mu \text{C}\]
\[Q_2=24\,\mu \text{C}\]
\[Q_3=72\,\mu \text{C}\]
\[Q_4=96\,\mu \text{C}\]
example:���Ĺq�e���p��

���q��
�b�ڭ̤W�����Q�פ��A����@�ӹq�e����Ӿ���A�]���a�����ʹq���Ӧb�����إ߹q���A�åB�x�s�R�q���C���鶡���Ŷ��O�u�Ū��A�]���ڭ̦b�Ҧ����������|�Ψ�@�ӯu�Ť��q�`��\(\varepsilon_0\)�ӭp��q�e���q�e�ȡC�{�b�ڭ̦Ҽ{�b�o�������ϰ��J�@�ǵ��t�����ơA���]�o�ӧ��ƬO���q�����Ҳզ��C���q������m�b�q�����A�q��������V�|����q�����v�T�ӫ��V�q������V�C�q���������Ҳ��ͪ��q���ѥ��q���ۭt�q�A�P�q��������V�ۤϡC�]���q�������q���P�q�e��ӱa�q�O�Ҳ��ͪ��q����V�ۤϡA�]����Ӿ��餧�����q���|�Q�q�����d�z�A�q���Q�d�z����ҧڭ̥Τ@�Ӥ��q�`�ƨӨ�e�q�����������C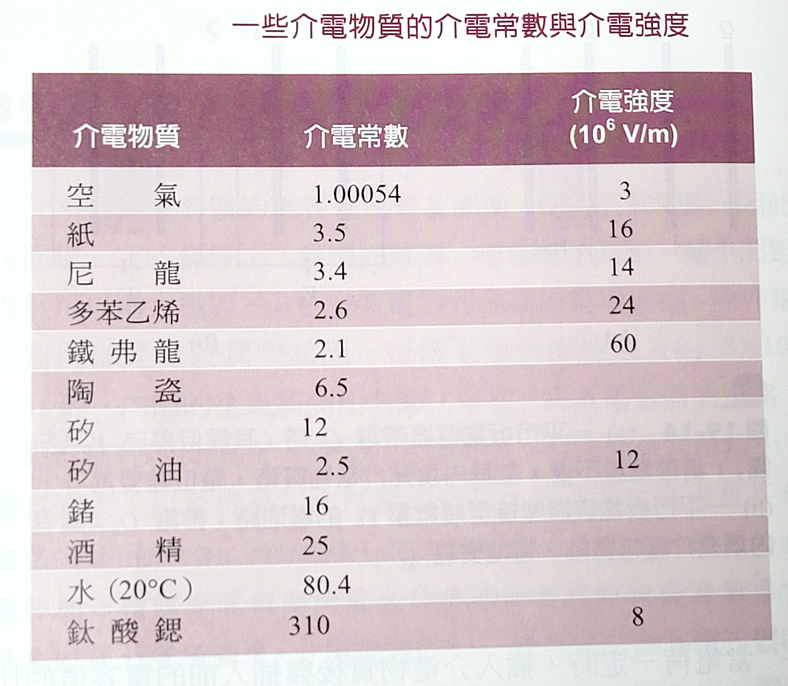 �o�ب㦳�q���������Ƨڭ̺٩I�����q��C��@�Ө㦳���q����ƪ��q�e�Ө��A��q�e�Ȥ]�|�o�ͧ��ܡA�ڭ̥��w�ʦa�Q�פ��q���q�e�Ȥj�p���v�T�C���]�ڭ̦��@�өt�ߪ��q�e�A�q�e����Ӿ���a��\(+q\)�M\(-q\)���q�q�A�{�b�ڭ̱N�@�Ӥ��q�贡�J��Ӿ��餧���A���]���q�觹���R���o�ӪŶ��A�q�����ϥ���O�������q���U���A�⥭��O���q��t�]�H���U���C���O�q���O�t�ߪ��S���y���A�]���ھڹq�e���w�q�G
\[C'=\dfrac{Q}{V}=\dfrac{Q}{V/\kappa} \Rightarrow C'=\kappa C\]
�q��t�a�U���A�y���q�e���ܤj�A�q�e���ܤj�����\(\kappa\)�N�O�o�Ӥ��q�誺���q�`�ơA�o�ӼƨèS�����(���q�`��,\(\kappa\)=�۹�q�e�v�A\(\varepsilon_{\text{r}}=\dfrac{\varepsilon}{\varepsilon_0}\))�C�b�k������������A�ڭ̳��C�F�`�����誺���q�`�ƩM���q�j�סC
�o�ب㦳�q���������Ƨڭ̺٩I�����q��C��@�Ө㦳���q����ƪ��q�e�Ө��A��q�e�Ȥ]�|�o�ͧ��ܡA�ڭ̥��w�ʦa�Q�פ��q���q�e�Ȥj�p���v�T�C���]�ڭ̦��@�өt�ߪ��q�e�A�q�e����Ӿ���a��\(+q\)�M\(-q\)���q�q�A�{�b�ڭ̱N�@�Ӥ��q�贡�J��Ӿ��餧���A���]���q�觹���R���o�ӪŶ��A�q�����ϥ���O�������q���U���A�⥭��O���q��t�]�H���U���C���O�q���O�t�ߪ��S���y���A�]���ھڹq�e���w�q�G
\[C'=\dfrac{Q}{V}=\dfrac{Q}{V/\kappa} \Rightarrow C'=\kappa C\]
�q��t�a�U���A�y���q�e���ܤj�A�q�e���ܤj�����\(\kappa\)�N�O�o�Ӥ��q�誺���q�`�ơA�o�ӼƨèS�����(���q�`��,\(\kappa\)=�۹�q�e�v�A\(\varepsilon_{\text{r}}=\dfrac{\varepsilon}{\varepsilon_0}\))�C�b�k������������A�ڭ̳��C�F�`�����誺���q�`�ƩM���q�j�סC���q�誺���ƪ���z(�q�l���ơB��l���ơB���V����)�i�H�ѦҺ���ʬ쪺���e�G���q��(wiki)
�b�q�Ͼ��ءA���q���T���~�q�����I�[�ӹq���ƪ��Ŷq�A�٬��q�e�v�C�b�D�u�Ť��ѩq��Q�q���ơA�b���褺�����`�q���|��p�C�q�e�v���Y�줶�q��ǿ�]�ήe�\�^�q������O�C�q�e�v�Ŷq�q����˼v�T���q��A��˳Q���q��v�T�C�q�e�v�S�٬��u����q�e�v�v�C�q�첾(\(\mathbf{D}=\varepsilon_{0}\mathbf{E} +\mathbf{P}; \quad \mathbf{P}=���ƪ��q���Ʊj��\))�P�q�������Y��{����
\[\mathbf{D} =\varepsilon \mathbf{E}; \]
�䤤�A\( \varepsilon \) �O�q�e�v�C���u�ʤ���A�q�e�v�P�u�Źq�e�v����v�A�٬��۹�q�e�v�A\(\varepsilon_{\text{r}}\)�G
\[ \varepsilon_{\text{r}}=\frac{\varepsilon}{\varepsilon_{0}}\]
�Ъ`�N�A�o�����u���b�R��B�s�W�v�����p�~���ߡC
���U�V���ʧ��ơA�۹�q�e�v�O�ӱi�q�F���U�V�P�ʧ��ơA�۹�q�e�v�O�Ӽжq�C���u�ʤ��q��A�q���Ʊj��\( \mathbf{P}\)�P�q��\(\mathbf{E}\)������G \[\mathbf{P} =\chi_{\text{e}} \varepsilon_{0}\mathbf{E}\] �N�o��{���N�J�q�첾���w�q���A�i�H�o��q�첾�P�q�������Y���G \[\mathbf{D} =(1+\chi_{\text{e}})\varepsilon_{0}\mathbf{E}\] �ҥH�A�q�e�v�P�q���Ʋv�����Y���� \[ \varepsilon =(1+\chi_{\text{e}})\varepsilon_{0}\] �b�@�몺���ΤW�ڭ̷|��۹�q�e�v�s�����q�`��\(\kappa\) \[\kappa=\varepsilon_{\text{r}}=(1+\chi_{\text{e}}); \quad C'=\kappa C; E'=E/\kappa; V'=V/\kappa\] \(\kappa\)�٬����q�`��(dielectric constant)�A�o�ӼƨèS�����C
���q��(wiki)
���U�V���ʧ��ơA�۹�q�e�v�O�ӱi�q�F���U�V�P�ʧ��ơA�۹�q�e�v�O�Ӽжq�C���u�ʤ��q��A�q���Ʊj��\( \mathbf{P}\)�P�q��\(\mathbf{E}\)������G \[\mathbf{P} =\chi_{\text{e}} \varepsilon_{0}\mathbf{E}\] �N�o��{���N�J�q�첾���w�q���A�i�H�o��q�첾�P�q�������Y���G \[\mathbf{D} =(1+\chi_{\text{e}})\varepsilon_{0}\mathbf{E}\] �ҥH�A�q�e�v�P�q���Ʋv�����Y���� \[ \varepsilon =(1+\chi_{\text{e}})\varepsilon_{0}\] �b�@�몺���ΤW�ڭ̷|��۹�q�e�v�s�����q�`��\(\kappa\) \[\kappa=\varepsilon_{\text{r}}=(1+\chi_{\text{e}}); \quad C'=\kappa C; E'=E/\kappa; V'=V/\kappa\] \(\kappa\)�٬����q�`��(dielectric constant)�A�o�ӼƨèS�����C
���q��(wiki)
�d��-1�G�P�߲y�q�e�A�P�b�q�l�q�e
�P�߲y�q�e
|
�P�b�q�l�q�e
|
�d��-2�G�q�e���ݤ��a�q�����p��
|
In the figure, switch S is closed to connect the uncharged capacitor of capacitance \(C = 0.25 \mu\)F to the battery of potential difference \(V = 12\) V. The lower capacitor plate has thickness \(L = 0.50\) cm and face area \(A = 2.0 \times 10^{-4}\) m2, and it consists of copper, in which the density of conduction electrons is \(n = 8.49 \times 10^{28}\) electrons/m3. From what depth \(d\) within the plate (figure) must electrons move to the plate face as the capacitor becomes charged? �Ϥ��A�}��S���X�A�N�q�e\(C = 0.25\mu\)F�����R�q�q�e���s����q��t\(V = 12\)V���q���C�U�q�e���O���p��\(L = 0.50\) cm �����n\(A = 2.0 \times 10^{-4}\) m2�A�ѻɲզ��A�䤤�Ǿɹq�l���K��\(n = 8.49 \times 10^{28}\) �ӹq�l/m3�C ���q�e���R�q�ɡA�q�l�����q�O�]�ϡ^��������`�� \(d\) ���ʨ�O���H |
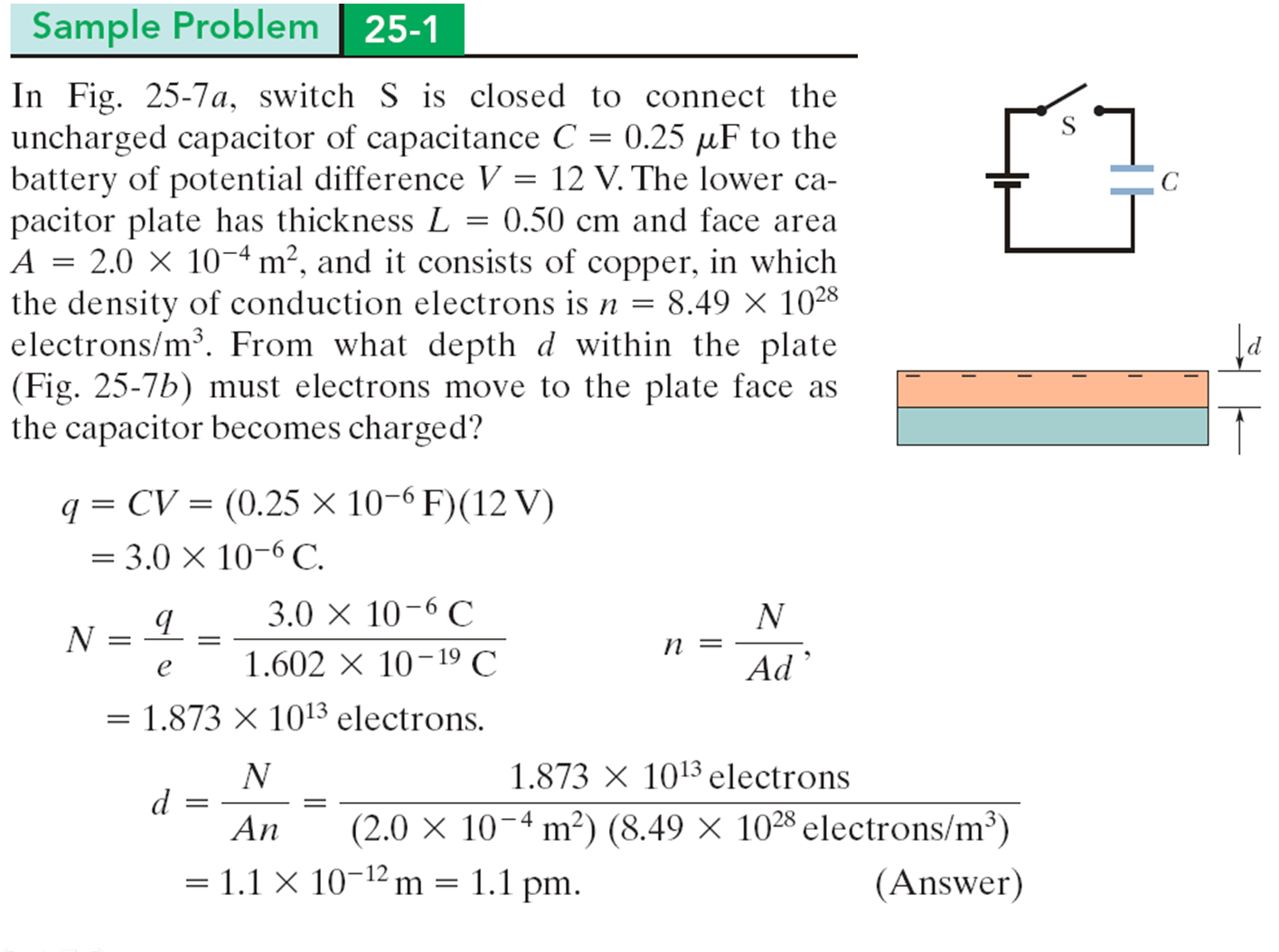
|
�d��-3�G���Ĺq�e���p��
|
(a) Find the equivalent capacitance for the combination of capacitances shown in the figure, across which potential difference \(V\) is applied. Assume
\[C_1 =12.0 \mu\text{F}, \, C_1 =5.3 \mu\text{F},\, \text{and} \, C_1 =4.5 \mu\text{F}.\]
(b) The potential difference applied to the input terminals in the figure is \(V= 12.5\) V. What is the charge on \(C_1\)? (a) �D�Ϥ��ҥܹq�e�զX�����Ĺq�e�A�b��W�I�[�q��t \(V\)�C �{�� \[C_1 =12.0 \mu\text{F}, \, C_1 =5.3 \mu\text{F},\, \text{and} \, C_1 =4.5 \mu\text{F}.\] (b) �Ϥ���J�ݪ��q��t��\(V= 12.5\) V�C\(C_1\) �W���q���O�h�֡H |

|
�d��-4�G�q�����s���G
|
Capacitor 1, with \(C1=3.55 \, \mu\)F, is charged to a potential difference \(V+0=6.30\) V, using a 6.30 V battery. The battery is then removed, and the capacitor is connected as in the figure to an uncharged capacitor 2, with \(C_2=8.95 \, \mu\)F. When switch S is closed, charge flows between the capacitors. Find the charge on each capacitor when equilibrium is reached. \(C1=3.55\,\mu\)F ���q�e�� 1 �ϥ� 6.30 V �q���R�q�ܹq��t \(V+0=6.30\) V�C �M����X�q���A�p�ϩҥܱN�q�e���s���쥼�R�q���q�e�� 2�A�䤤 \(C_2=8.95 \, \mu\)F�C ���}�� S ���X�ɡA�q���b�q�e�������y�ʡC ���F�쥭�ŮɡA��X�C�ӹq�e���W���q���C |

|
�d��-6
|
An isolated conducting sphere whose radius \(R\) is 6.85 cm has a charge \(q = 1.25\) nC. (a) How much potential energy is stored in the electric field of this charged conductor? (b) What is the energy density at the surface of the sphere? �b�| \(R\) �� 6.85 cm ���t�߾ɹq�y��㦳�q�� \(q = 1.25\) nC�C (a) �o�ӱa�q���骺�q�����x�s�F�h�ֶկ�H (b) �y���������q�K�O�h�֡H |

|
�d��-7
|
A parallel-plate capacitor whose capacitance \(C\) is 13.5 pF is charged by a battery to a potential difference \(V = 12.5\) V between its plates. The charging battery is now disconnected, and a porcelain slab ((\kappa=6.50\)) is slipped between the plates. (a) What is the potential energy of the capacitor before the slab is inserted? (b) What is the potential energy of the capacitorslab device after the slab is inserted? �q�e \(C\) �� 13.5 pF ������O�q�e���ѹq���R�q�ܨ䷥�O�������q��t \(V = 12.5\) V�C �R�q�q���{�b�w�_�}�A�@�����O ((\kappa=6.50\)) �b�O�����ưʡC (a) ���J���O���e�q�e�����կ�O�h�֡H (b) �O�����J��A�q�e���O�˸m���կ�O�h�֡H |

|
�d��-8
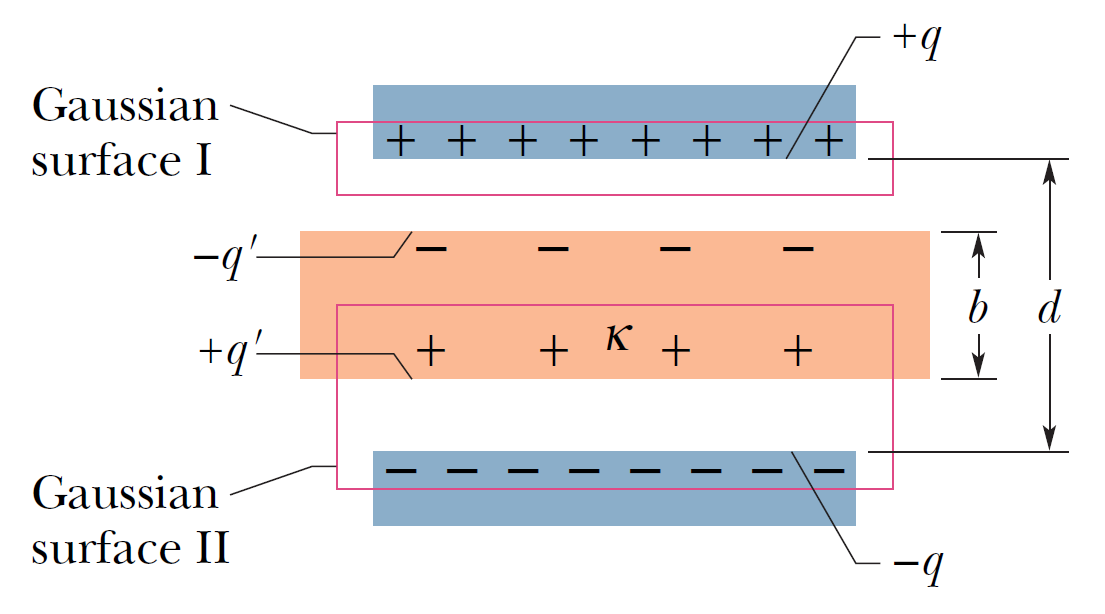 |

|
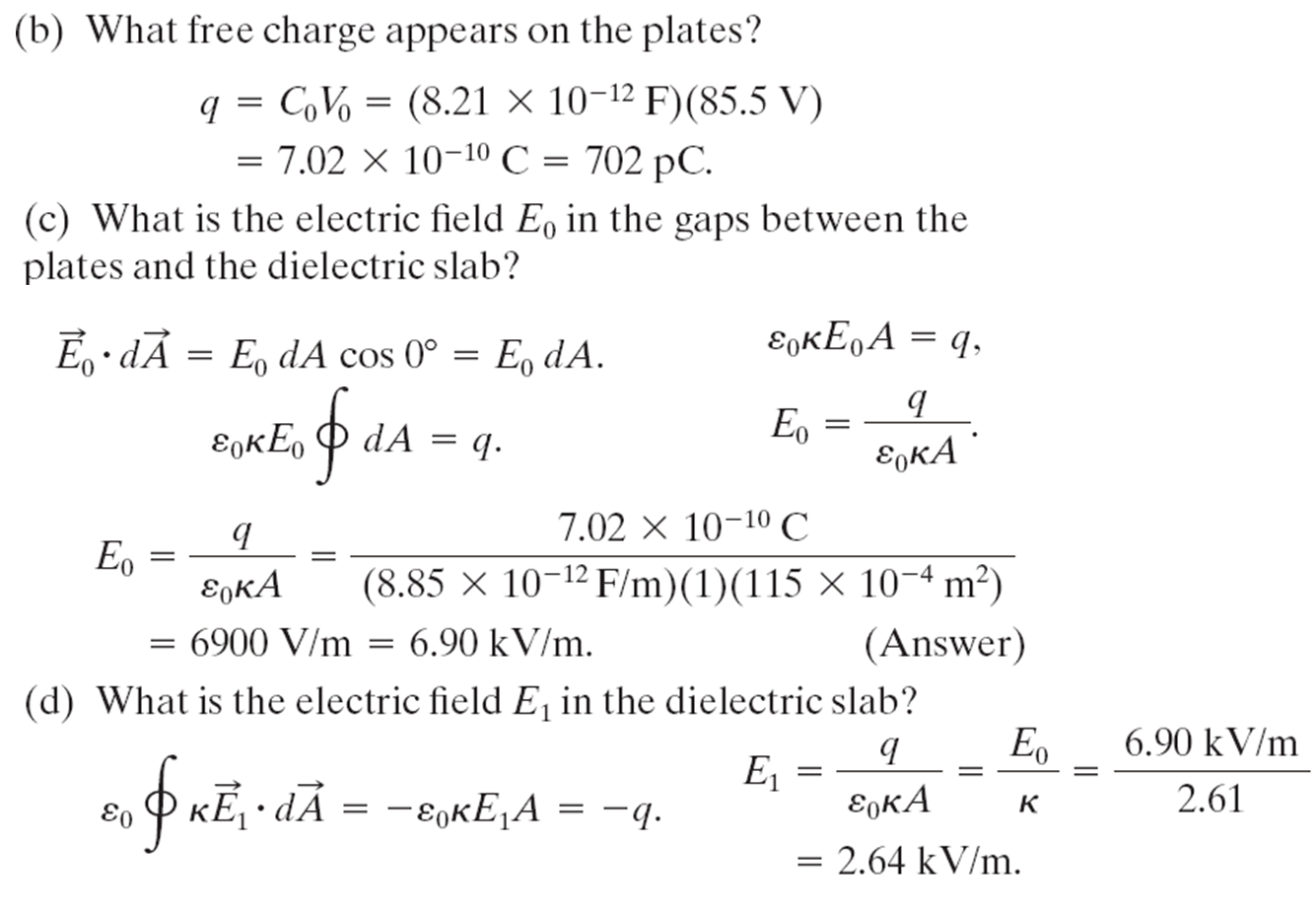
|

|
�½ұЮv
���é� ycchen@thu.edu.tw