電路
你被電路包圍。您可能會為自己擁有的電子設備數量感到自豪,甚至可能會在腦海中列出您希望擁有的設備。這些設備中的每一個,以及為您的家庭供電的電網,都依賴於現代電氣工程。我們無法輕易估計電氣工程及其產品當前的財務價值,但我們可以肯定,隨著越來越多的任務以電氣方式處理,其財務價值每年都在增長。收音機現在是電子調諧而不是手動調諧。信息現在通過電子郵件而不是通過郵政系統發送。研究期刊現在可以在計算機上閱讀,而不是在圖書館大樓裡閱讀,研究論文現在以電子方式複制和歸檔,而不是影印並塞進文件櫃。電氣工程的基礎科學是物理學。在本章中,我們將介紹由電阻器和電池以及電容器組合而成的電路的物理特性。我們將討論直流電路,電荷限制在沿一個方向流過的電路。電動勢
用導線將兩個帶電的導體相連時,導線上會出現短暫的電流,但是當兩個導體間的電位差變為零的時候,電流就停止。同理,一個蓄電的電容器也只能提供短暫的電流,純粹靠靜電的方式並不能提供持續的電流。要建立一個持續的電流,必須有一個完整、封閉的導電通路,而且在通路上必須有可以對電流載子做功,能夠使電流從低電位移往高電位的裝置存在。顯然,這種對載流子做功的機制,必須是有一有別於靜電的方式。金屬導線有電阻,有電阻的裝置在電路學上通常以這個符號表示。化學電池也可以對導電電子做功,稱為電動勢,通常以這個符號來表示。長線代表電位較高的正極,短線代表電位較低的負極。有電阻的元件稱為一個電阻器。假如我們把一個電阻器的兩端,連接到一個化學電池的正負極,以電路的符號表示如圖。右圖所顯示的電路圖代表一個完整的導電通路,而導電電子為電流載子,電阻器以及用以連接導線固然是導電的介質,電池的內部也可以導電。圖中所顯示的電路中,電流載子是帶負電的導電電子,但習慣上我們用帶有正電的粒子說明電流的現象,正電荷從電池的正極上出發,經導線電阻器再到電池的負極上,經過電池的內部又回到正極上。電池在正負極之間維持一定的電位差,當正電荷在負極上時其能量減少,從負極上進入電池的內部後,必須由電池做功,才能從電位較低的負極,經電池內部回到電位較高的正極,因此經過這樣的循環,就可以形成持續的電流。當有\(dq\)的正電荷流經過電池的內部,而電池對電荷作功\(dW\),可以下面的方程式表示 \[dW=\mathscr{E} dq\] \(\mathscr{E}\)稱為電池的電動勢。電動勢可定義為電池對通過其內部的單位正電荷所做的功,電動勢的因次和電位差相同,因此電動勢的單位也是以伏特表示。電流在只在電池的內部流通時,它從電動勢所獲得的能量會有部分損失,也就是電池的內部對電流而言有電阻,這種電阻稱為電池的內電阻。內電阻通常以符號\(r\)表示,所以嚴格說,一個電池在電路上的符號應該用一個沒有內電阻電動勢\(\mathscr{E}\)串聯一個電阻\(r\)的電阻器表示之。當一個電阻為\(R\)的電阻器和一個化學電池串聯時,其正確的電路表示法應該如右圖所示。當有\(dq\)的電荷在\(dt\)的時間內,流經此電路一次,電池對其所做的功為\(\mathscr{E} dq\),而此電荷流經外電阻\(R\)及內電阻\(r\)時,所損失的能量就是焦耳熱,\(I^2 (R+r)dt\)。所以 \[\mathscr{E} dq=I^2 (R+r)dt\] 上面的方程式兩邊都用\(dt\)除之,可得 \[\mathscr{E}I=I^2 (R+r)\] 這個方程式表示在單位時間內電池對電流所做的功等於電路上的總焦耳熱。將方程式的兩邊都以電流\(I\)除之,可得 \[\mathscr{E}=I(R+r)\] 上面的方程式也可以表示成 \[ I=\dfrac{\mathscr{E}}{R+r} \] 電池正負極之間的電位差,稱為電池的端電壓(terminal voltage)。斷路時,也就是電池沒有連接到外電阻的時候,電流為0,此時電池的端電壓就是他的電動勢。但是當電池外接電阻時,電池兩端的電壓是\(\mathscr{E}-Ir\),\(I\)是當時流經過電池的電流,\(r\)是電池的內電阻。
當內電阻遠小於負載電阻時,\(r \ll R\),端電壓值會與電動勢非常接近,但是當電池使用一段時間之後,內電阻\(r\)會增加,若內電阻\(r\)的大小接近負載電阻\(R\)時,端電壓會明顯下降。因此可知,相同電動勢的電池,內電阻較小者,在相同負載下,可提供較大的電流,因而有較大的輸出功率。
HL27示例問題-1:電流迴路與電池內電阻
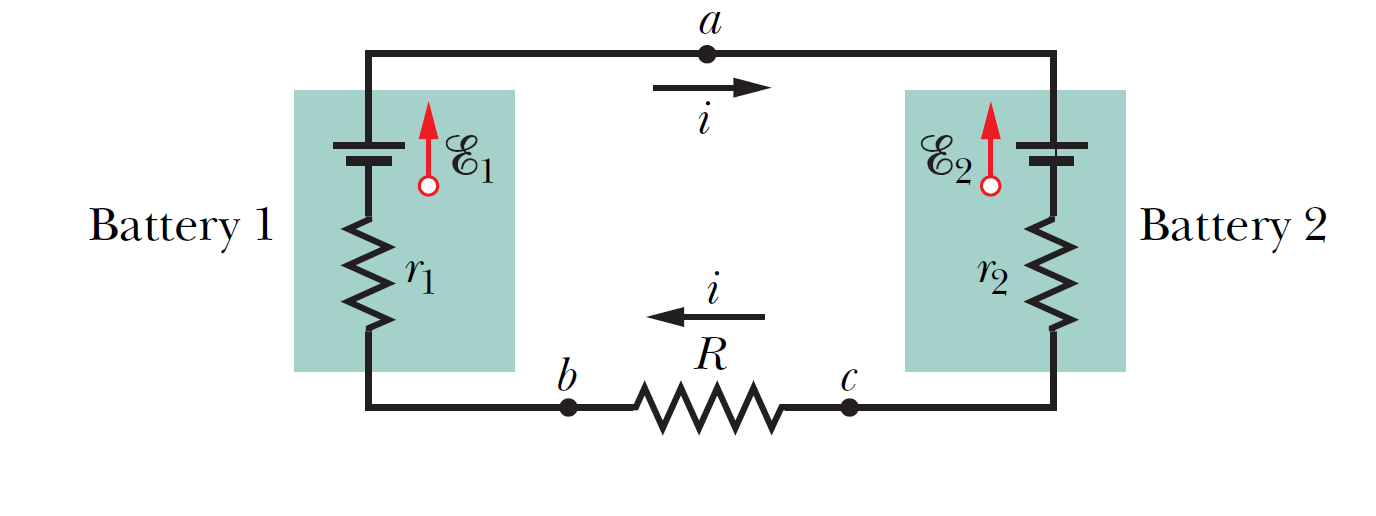 The emfs and resistances in the circuit of the figure have the following values:\[ \mathscr{E}_1= 4.4 V, \mathscr{E}_2= 2.1 V, \] \[r_1 = 2.3 \Omega, r_2 = 1.8 \Omega, R= 5.5 \Omega .\] (a) What is the current \(i\) in the circuit? (b) What is the potential difference between the terminals of battery 1 in the figure?
The emfs and resistances in the circuit of the figure have the following values:\[ \mathscr{E}_1= 4.4 V, \mathscr{E}_2= 2.1 V, \] \[r_1 = 2.3 \Omega, r_2 = 1.8 \Omega, R= 5.5 \Omega .\] (a) What is the current \(i\) in the circuit? (b) What is the potential difference between the terminals of battery 1 in the figure? 圖中電路中的電動勢和電阻值如下:\[ \mathscr{E}_1= 4.4 \,V,\quad \mathscr{E}_2= 2.1 \, V, \quad r_1 = 2.3 \, \Omega, \quad r_2 = 1.8 \, \Omega, \quad R = 5.5 \Omega .\] (a) 電路中的電流 \(i\) 是多少? (b) 圖中電池 1 的端子之間的電位差是多少?
\[-\mathscr{E}_1 + ir_1 + iR + ir_2 + \mathscr{E}_2=0 \] \[ i=\dfrac{\mathscr{E}_1 -\mathscr{E}_2}{R+r_1+r_2}=\dfrac{4.4-2.1}{5.5+2.3+1.8}=0.2396\,\text{A}\]
\[V_b - ir_1 + \mathscr{E}_1=V_a\] \[V_a - V_b = -ir_1 + \mathscr{E}_1=-(0.2396)(2.3)+4.4=3.84 \,\text{V} \]
電阻的串聯與並聯
當電路上有兩個電阻如圖所示的方式連結在一起時,我們稱這兩個電阻串聯。串聯的兩個電阻上有過相同的電流,這兩個串聯的電阻可用一個電阻取代,而不會影響a與b兩點間的電位差,以及電路其他部分流通的電流,這個電阻稱為等效電阻\(R_{eq}\)。令a與b兩點間的電位差為\(V_{ab}\),從圖中可以得到如下的公式 \[V_{ab}=IR_1 + IR_2 =I(R_1+R_2)\] 並且從等效電阻的電路圖可以得到 \[V_{ab}=IR_{eq}\] 比較上面兩個方程式,就可得到等效電阻, \[R_{eq}=R_1 + R_2 \] 電路中的兩個電阻如果像右圖的方式連接時,稱為並聯。並聯的兩個電阻有相同的電位差,並聯的兩個電阻也可用一個等效電阻來取代,並不會改變a與b兩點的電位差,以及電路其他部分流通的電流。從電路圖中我們可以得到 \[V_{ab}=I_1 R_1 = I_2 R_2 \] 其中的\(I_1, \, I_2\)分別是流過\(R_1, \, R_2\)的電流。因為電流不會在導線上或電阻器內產生或消滅,也就是電荷守恆,我們有下面的關係: \[ I=I_1 + I_2 \] 綜合上面的方程式我們可以得到等效電阻必須滿足的方程式如下: \[\dfrac{1}{R_{eq}}=\dfrac{1}{R_1}+\dfrac{1}{R_2} \] 並聯的等效電阻\(R_{eq}\)顯然小於分電阻\(R_1, \, R_2\)。並且 \[I_1 =\dfrac{V_{ab}}{R_1}; \, I_2 =\dfrac{V_{ab}}{R_2}; \, \dfrac{I_1}{I_2}=\dfrac{R_2}{R_1} \] 上面這個式子表示流經過兩個並聯電阻上的電流與分電阻的電阻值成反比。如果有兩個以上的電阻串聯等效電阻的公式為: \begin{equation} R_\text{series} = R_1 + R_2 + \cdots + R_N. \end{equation} 如果有兩個以上的電阻並聯等效電阻的公式為: \begin{equation} \frac{1}{R_\text{parallel} } = \frac{1}{R_{1}} + \frac{1}{R_{2}} + \cdots + \frac{1}{R_{N}}, \end{equation}
克希荷夫法則與多迴路電路
電路中一個完整封閉的電流通路,稱為一個迴路(loop)。一個電池的兩極連接是一個電阻的簡單電路,只有一個迴路。有兩個以上迴路的電路,稱為多迴路電路,右圖所示的就是一個多迴路的電路。abc的構成一個迴路,cdef也是一個迴路。有相同電流流過的路段,稱為一個分支(branch),右圖中有cd, bad,fed,3個分支。兩個分支的交點,稱為一個節點,如右圖中的d點。要完整解出右圖所示的電路,必須解出三個分支的電流\(I_1, \, I_2, \,I_3\)。克希荷夫法則(克希荷夫定律)可以解出多迴路電路的問題。克希荷夫法則有兩個, \[法則1:流入一個節點的總電流等於流出的總電流。\] \[法則2:一個迴路上的總電位差為0\] 法則1是源自於電荷守恆原理,也就是如果電荷不會在一個節點上產生或消滅,那麼在單位時間內流入該節點的電荷量,應等於流出的總電荷量。事實上,在討論兩個電阻並聯的等效電路時,我們已經應用的這個法則。我們在討論電池的內電阻的迴路時,已經應用過法則2,其中我們得到一個單一迴路中的電位差公式 \[\mathscr{E} -Ir -IR =0 \] 上式可用文字敘述如下:從b點出發,經過電動勢的電池後,電位升高了\(\mathscr{E}\)(從流經電路的正電荷的觀點來看),經過內電阻\(r\)後電位下降了\(Ir\),再經過外電阻\(R\)後,又下降\(IR\),到b點又回到了原來的電位。第二個法則也可敘述成一個迴路上的總電位升高等於總電位降落,這個法則其實就是靜電場是一個保守場的基本結果。對一個封閉的路徑作靜電場的路徑積分,必然是零,而路徑積分就是電位差,對一個封閉的迴路做電位差的計算,必然會得到零的結果,這也就是第二法則所敘述的內容。
HL27示例問題-2:多電流迴路-1
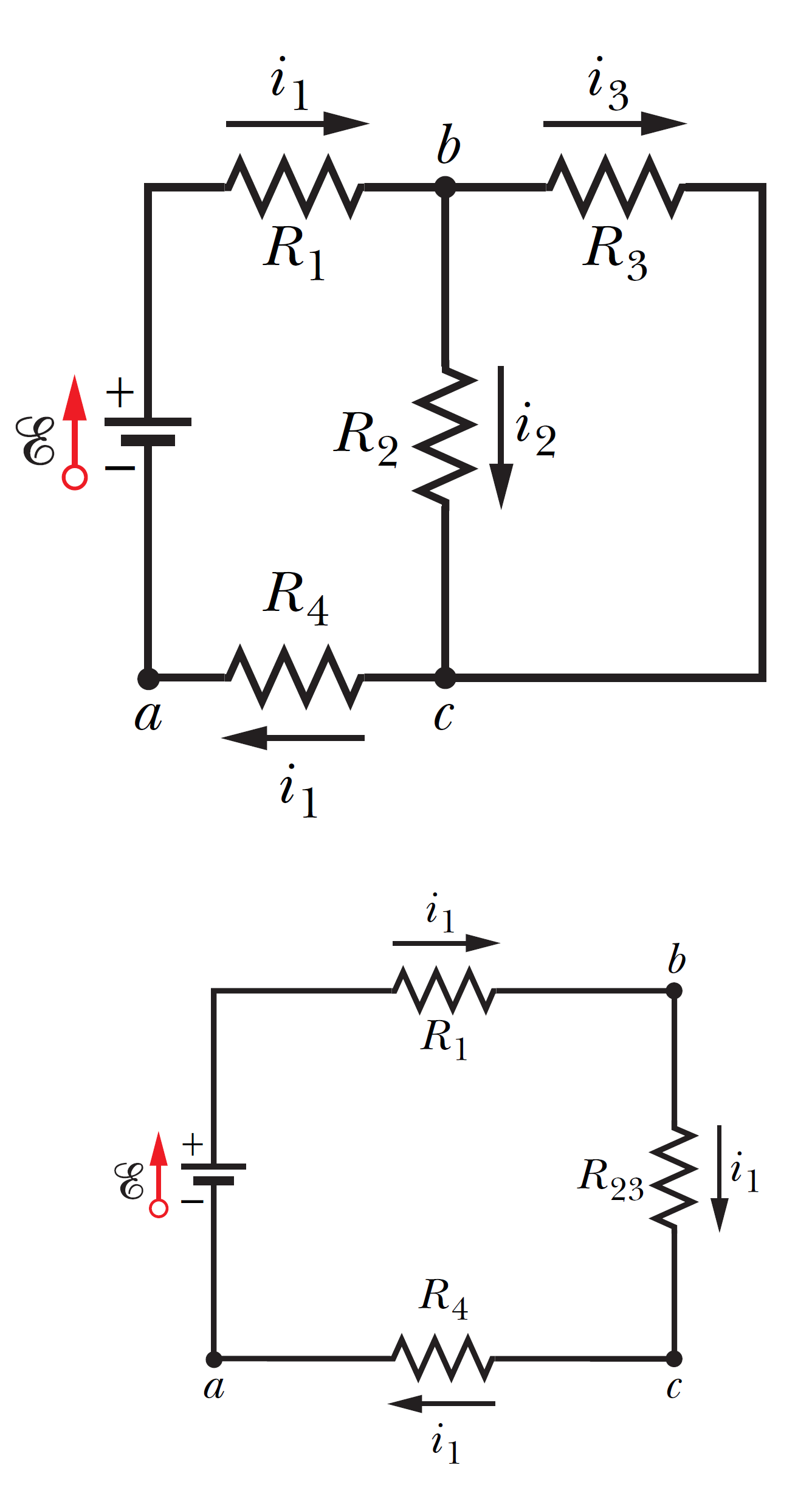 The figure shows a multiloop circuit containing one ideal battery and four resistances with the following values: \[R_1= 20 \, \Omega, \quad R_2= 20 \, \Omega,\] \[ \mathscr{E}=12 \,V, \quad R_3 = 30\, \Omega, \quad R_4= 8.0 \, \Omega.\] (a) What is the current through the battery? (b) What is the current \(i_2\) through \(R_2\)? (c) What is the current \(i_3\) through \(R_3\)?
The figure shows a multiloop circuit containing one ideal battery and four resistances with the following values: \[R_1= 20 \, \Omega, \quad R_2= 20 \, \Omega,\] \[ \mathscr{E}=12 \,V, \quad R_3 = 30\, \Omega, \quad R_4= 8.0 \, \Omega.\] (a) What is the current through the battery? (b) What is the current \(i_2\) through \(R_2\)? (c) What is the current \(i_3\) through \(R_3\)? 圖中顯示了一個包含一個理想電池和四個電阻的多迴路電路,其值如下: \[R_1= 20 \, \Omega, \quad R_2= 20 \, \Omega,\] \[ \mathscr{E}=12 \,V, \quad R_3 = 30\, \Omega, \quad R_4= 8.0 \, \Omega.\] (a) 通過電池的電流是多少? (b) 到\(R_2\) 的電流\(i_2\) 是多少? (c) 到\(R_3\) 的電流\(i_3\) 是多少?
(a)
\[R_{23}=\dfrac{R_2R_3}{R_2+R_3}=\dfrac{(20)(30)}{20+30}=12 \,\Omega\] \[+\mathscr{E}-i_1R_1-i_1R_{23}-i_1R_4=0, \quad i_1=0.3 \,\text{A}.\] (b)
\[V_2=V_3=V_{23}=i_1 R_{23}=(0.3)(12)=3.6 \,\text{V}\] \[i_2=\dfrac{V_2}{R_2}=\dfrac{3.6}{20}=0.18 \,\text{A}\] (c)
\[i_3=i_1 - i_2=0.3-0.18=0.12 \,\text{A}\]
HL27示例問題-3:多電流迴路-2
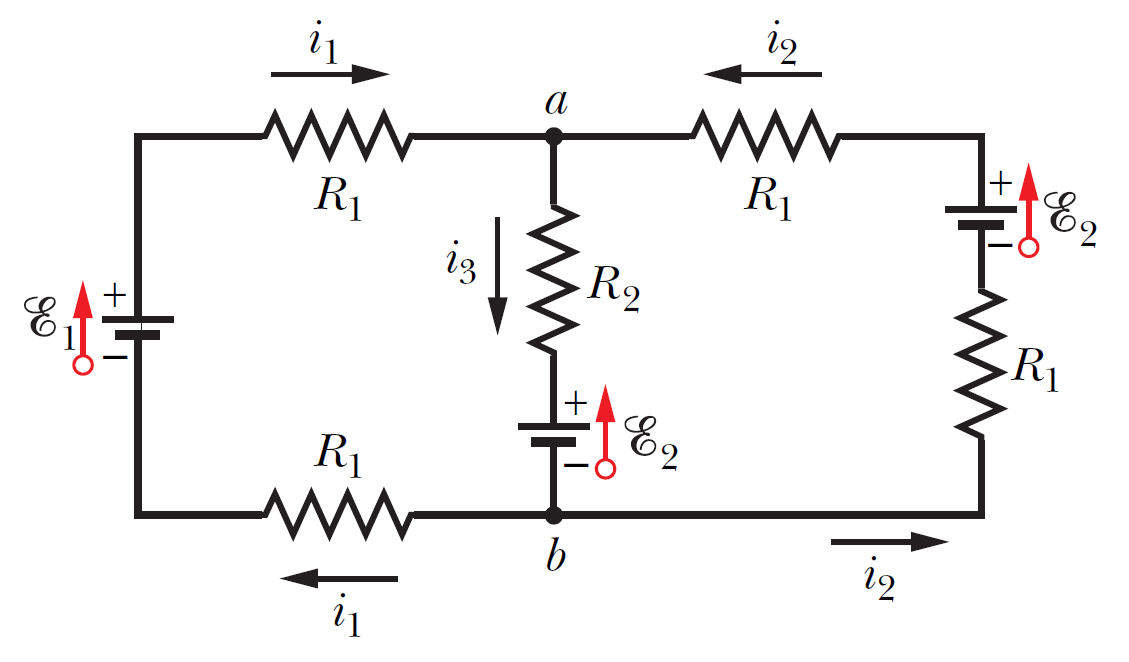 The figure shows a circuit whose elements have the following values: \[ \mathscr{E}_1= 3.0 \,V, \quad \mathscr{E}_2= 6.0 \, V, \] \[ R_1 = 2.0 \, \Omega, \quad R_2 = 4.0 \, \Omega.\] The three batteries are ideal batteries. Find the magnitude and direction of the current in each of the three branches.
The figure shows a circuit whose elements have the following values: \[ \mathscr{E}_1= 3.0 \,V, \quad \mathscr{E}_2= 6.0 \, V, \] \[ R_1 = 2.0 \, \Omega, \quad R_2 = 4.0 \, \Omega.\] The three batteries are ideal batteries. Find the magnitude and direction of the current in each of the three branches. 圖中顯示了一個電路,其元素具有以下值: \[ \mathscr{E}_1= 3.0 \,V,\quad \mathscr{E}_2= 6.0 \, V, \] \[R_1 = 2.0 \, \Omega, \quad R_2 = 4.0 \, \Omega.\] 三節電池為理想電池。 找出三個分支中每個分支中電流的大小和方向。
\[\text{left loop: } -i_1R_1+\mathscr{E}_1-i_1R_1-(i_1+i_2)R_2-\mathscr{E}_2=0\] \[ 8i_1+4i_2=-3 \tag{i}\] \[\text{right-hand loop: } -i_2R_1+\mathscr{E}_2-i_2R_1-(i_1+i_2)R_2-\mathscr{E}_2=0\] \[4i_1+8i_2=0 \tag{ii}\] \[\text{combine eq.(i) and eq.(ii): } i_1=-0.5 \,\text{A}\] \[i_2=0.25 \,\text{A}, \quad i_3=-0.25 \, \text{A}\] The positive answer we obtained for \(i_2\) signals that our choice of direction for that current is correct. However, the negative answers for \(i_1\) and \(i_3\) indicate that our choices for those currents are wrong.
\(i_2\) 獲得"+"的答案表明我們對該電流的方向選擇是正確的。 然而,\(i_1 \lt 0\) 和 \(i_3 \lt 0\) 的答案表明我們對這些電流的選擇是錯誤的。
example
|
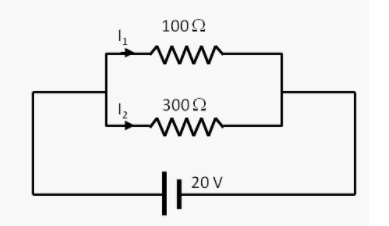
考慮此電路:
|
(a) 75 % , 25 % , (b) 75 Ω (c) 267 mA , (d) 67 mA , 200 mA
example
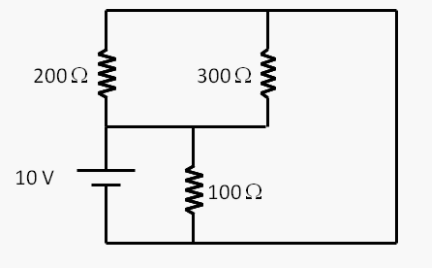
|
考慮此電路:求通過圖中給出的電路中每個電阻器的電流。 |
如果你仔細的觀察每一個電阻的連接情況,不難發現每一個電阻的兩端都接上了電池的兩端,因此三個電阻和電池並聯,每一個電阻的電位差都是電池的電位差10伏特,因此不難算出每個電阻的電流分別如下:
\begin{equation}
\frac{10}{100}=\frac{1}{10}\text{ A},\ \frac{10}{200}=\frac{1}{20}\text{ A},\ \frac{10}{300}=\frac{1}{30}\text{ A}
\end{equation}
example
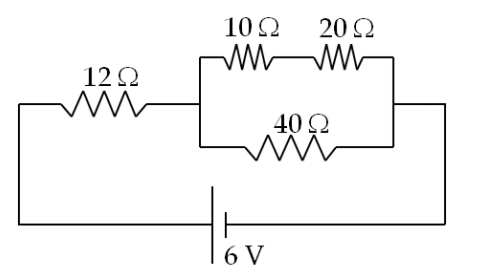
|
考慮連接到電壓源的四個電阻器,如電路所示。 找出通過每個電阻器的電流。 |
\begin{equation}
\phi_d= 0; \phi_a = 6\ \text{V}; \phi_b = \dfrac{60}{17}\ \text{V}; \phi_c = \dfrac{40}{17}\ \text{V}. I_1 = \dfrac{2}{7}\ \text{A}; I_2 = \dfrac{3}{34}\ \text{A}; I = \dfrac{7}{34}\ \text{A}.
\end{equation}
============Solution:=============
To find current through the resistors, we need potential drop across each. Therefore, we start with labeling the node potential points on the circuit as shown in the figure. As explained above, the node points represent points of unique electric potential values. There are four nodes in the given circuit, which are labeled \(a\text{,}\) \(b\text{,}\) \(c\text{,}\) and \(d\text{.}\) Node \(d\) is connected to the negative of the source and is usually set zero volt as reference, \(\phi_d = 0\text{.}\) Since voltage of the battery is 6 volts, the potential at \(a\) is 6 V, that is, \(\phi_a = 0\text{.}\) Now, we follow step-by-step procedure of simplifying the circuit to find the potentials at \(b\) and \(c\text{,}\) viz., \(\phi_b\) and \(\phi_c\text{,}\) respectively.
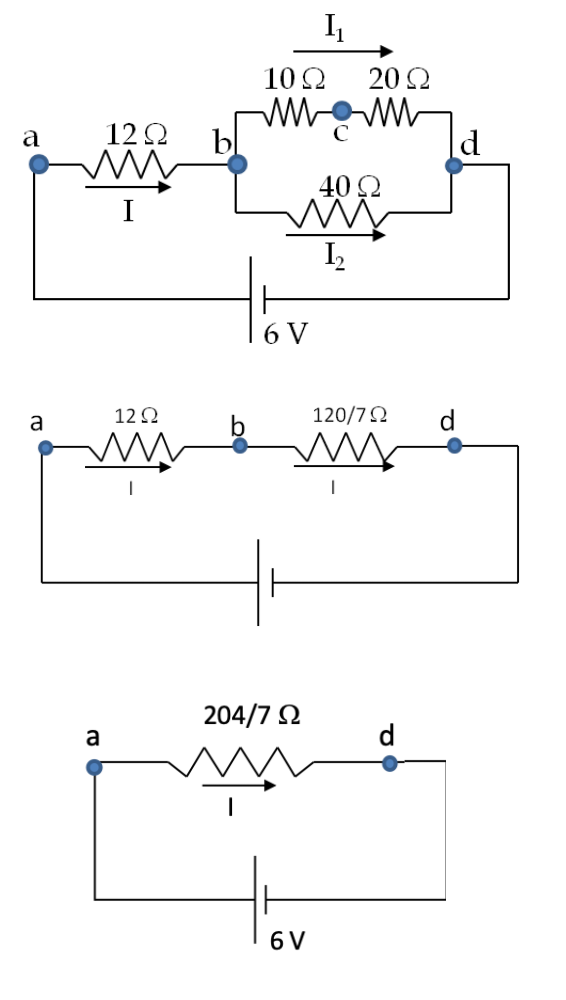 Step 1:
Step 1:
If any resistors in series, replace them by their equivalent resistors. Here only \(10\ \Omega\) and \(20\ \Omega\) are in series. Therefore, we replace them by a \(30\text{-}\Omega\) resistor. It is best to keep the same labels here as in the previous diagram.
Step 2:
If any resistors in parallel, replace them by equivalent resistors. Here only 30 \(\Omega\) and 40 \(\Omega\) are in parallel. Therefore, we replace the combination by their equivalent resistance, which is \(\dfrac{120}{7}\ \Omega\text{.}\)
Step 3:
After replacing the parallel resistors by \(\dfrac{120}{7}\ \Omega\text{,}\) we find that it is in series with the \(12\text{-}\Omega\) resistor. Therefore current through the \(\dfrac{120}{7}\ \Omega\) must be same as that goes through the \(12\text{-}\Omega\) resistor. Now the two resistors in series can be replaced by a \(\dfrac{204}{7}\text{-}\Omega\) resistor resulting in a really simple circuit. The current through the \(\dfrac{204}{7}\text{-}\Omega\) resistor must be same as the \(12\text{-}\Omega\) or \(\dfrac{120}{7}\text{-} \Omega\) resistor since it is replacing resistors in series.
Step 4:
Now, we can use Ohm's law to find the current through \(\dfrac{204}{7}\text{-}\Omega\) resistor. \begin{equation*} I = \dfrac{6V}{(204/7)\Omega} = \dfrac{7}{34}\ \text{A}. \end{equation*} Step 5:
We then trace our path backwards towards the original circuit. The current through the \(12\text{-}\Omega\) resistor is also \(7/34\text{ A}\text{.}\) Therefore, potential drop across the \(12\text{-}\Omega\) resistor i \begin{equation*} \phi_a-\phi_b = \dfrac{7}{34}\ \text{A} \times 12\ \Omega = \dfrac{42}{17}\ \text{V}. \end{equation*} The potential drop across the \(\dfrac{120}{7}\text{-} \Omega\) resistor is \((60/17)\text{V}\text{.}\) \begin{equation*} \phi_b-\phi_d = \dfrac{7}{34}\ \text{A} \times \dfrac{120}{7}\ \Omega = \dfrac{60}{17}\ \text{V}\ \ \Longrightarrow\ \phi_b = \dfrac{60}{17}\ \text{V}. \end{equation*} Going back one more step we find that potential drop across the \(30\text{-}\Omega\) resitor is same as that across the \(\dfrac{120}{7}\text{-}\Omega\) resistor we worked out. Hence, current through the \(30\text{-}\Omega\) resistor is simply \begin{equation*} I_1 = \dfrac{(60/17)\ \text{V}}{30\ \Omega} = \dfrac{2}{17}\ \text{A} \end{equation*} Therefore, voltage \(\phi_c\) is obtained from the potential drop across the \(20\text{-} \Omega\) resistor as given by \begin{equation*} \phi_c - \phi_d = \left( \dfrac{2}{17}\ \text{A} \right) \times 20\ \Omega = \dfrac{40}{17}\ \text{V}. \end{equation*} Since \(\phi_d = 0\text{,}\) we obtain \(\phi_c = \dfrac{40}{17}\ \text{V}\text{.}\) We can use the node voltages to obtain the current through various resistors. Alternately, since the total current \(I\) was split into \(I_1\) and \(I_2\text{,}\) we can find \(I_2\) by subtracting \(I_1\) from \(I\text{.}\) \begin{equation*} I_2 = I - I_1 = \dfrac{7}{34}\ \text{A} - \dfrac{2}{17}\ \text{A} = \dfrac{3}{34}\ \text{A} \end{equation*} Summarizing the answer: \begin{align*} \amp \phi_d= 0;\ \phi_a = 6\ \text{V};\ \phi_b = \dfrac{60}{17}\ \text{V};\ \phi_c = \dfrac{40}{17}\ \text{V}.\\ \amp I_1 = \dfrac{2}{7}\ \text{A};\ I_2 = \dfrac{3}{34}\ \text{A};\ I = \dfrac{7}{34}\ \text{A}. \end{align*}
To find current through the resistors, we need potential drop across each. Therefore, we start with labeling the node potential points on the circuit as shown in the figure. As explained above, the node points represent points of unique electric potential values. There are four nodes in the given circuit, which are labeled \(a\text{,}\) \(b\text{,}\) \(c\text{,}\) and \(d\text{.}\) Node \(d\) is connected to the negative of the source and is usually set zero volt as reference, \(\phi_d = 0\text{.}\) Since voltage of the battery is 6 volts, the potential at \(a\) is 6 V, that is, \(\phi_a = 0\text{.}\) Now, we follow step-by-step procedure of simplifying the circuit to find the potentials at \(b\) and \(c\text{,}\) viz., \(\phi_b\) and \(\phi_c\text{,}\) respectively.
 Step 1:
Step 1:If any resistors in series, replace them by their equivalent resistors. Here only \(10\ \Omega\) and \(20\ \Omega\) are in series. Therefore, we replace them by a \(30\text{-}\Omega\) resistor. It is best to keep the same labels here as in the previous diagram.
Step 2:
If any resistors in parallel, replace them by equivalent resistors. Here only 30 \(\Omega\) and 40 \(\Omega\) are in parallel. Therefore, we replace the combination by their equivalent resistance, which is \(\dfrac{120}{7}\ \Omega\text{.}\)
Step 3:
After replacing the parallel resistors by \(\dfrac{120}{7}\ \Omega\text{,}\) we find that it is in series with the \(12\text{-}\Omega\) resistor. Therefore current through the \(\dfrac{120}{7}\ \Omega\) must be same as that goes through the \(12\text{-}\Omega\) resistor. Now the two resistors in series can be replaced by a \(\dfrac{204}{7}\text{-}\Omega\) resistor resulting in a really simple circuit. The current through the \(\dfrac{204}{7}\text{-}\Omega\) resistor must be same as the \(12\text{-}\Omega\) or \(\dfrac{120}{7}\text{-} \Omega\) resistor since it is replacing resistors in series.
Step 4:
Now, we can use Ohm's law to find the current through \(\dfrac{204}{7}\text{-}\Omega\) resistor. \begin{equation*} I = \dfrac{6V}{(204/7)\Omega} = \dfrac{7}{34}\ \text{A}. \end{equation*} Step 5:
We then trace our path backwards towards the original circuit. The current through the \(12\text{-}\Omega\) resistor is also \(7/34\text{ A}\text{.}\) Therefore, potential drop across the \(12\text{-}\Omega\) resistor i \begin{equation*} \phi_a-\phi_b = \dfrac{7}{34}\ \text{A} \times 12\ \Omega = \dfrac{42}{17}\ \text{V}. \end{equation*} The potential drop across the \(\dfrac{120}{7}\text{-} \Omega\) resistor is \((60/17)\text{V}\text{.}\) \begin{equation*} \phi_b-\phi_d = \dfrac{7}{34}\ \text{A} \times \dfrac{120}{7}\ \Omega = \dfrac{60}{17}\ \text{V}\ \ \Longrightarrow\ \phi_b = \dfrac{60}{17}\ \text{V}. \end{equation*} Going back one more step we find that potential drop across the \(30\text{-}\Omega\) resitor is same as that across the \(\dfrac{120}{7}\text{-}\Omega\) resistor we worked out. Hence, current through the \(30\text{-}\Omega\) resistor is simply \begin{equation*} I_1 = \dfrac{(60/17)\ \text{V}}{30\ \Omega} = \dfrac{2}{17}\ \text{A} \end{equation*} Therefore, voltage \(\phi_c\) is obtained from the potential drop across the \(20\text{-} \Omega\) resistor as given by \begin{equation*} \phi_c - \phi_d = \left( \dfrac{2}{17}\ \text{A} \right) \times 20\ \Omega = \dfrac{40}{17}\ \text{V}. \end{equation*} Since \(\phi_d = 0\text{,}\) we obtain \(\phi_c = \dfrac{40}{17}\ \text{V}\text{.}\) We can use the node voltages to obtain the current through various resistors. Alternately, since the total current \(I\) was split into \(I_1\) and \(I_2\text{,}\) we can find \(I_2\) by subtracting \(I_1\) from \(I\text{.}\) \begin{equation*} I_2 = I - I_1 = \dfrac{7}{34}\ \text{A} - \dfrac{2}{17}\ \text{A} = \dfrac{3}{34}\ \text{A} \end{equation*} Summarizing the answer: \begin{align*} \amp \phi_d= 0;\ \phi_a = 6\ \text{V};\ \phi_b = \dfrac{60}{17}\ \text{V};\ \phi_c = \dfrac{40}{17}\ \text{V}.\\ \amp I_1 = \dfrac{2}{7}\ \text{A};\ I_2 = \dfrac{3}{34}\ \text{A};\ I = \dfrac{7}{34}\ \text{A}. \end{align*}
example
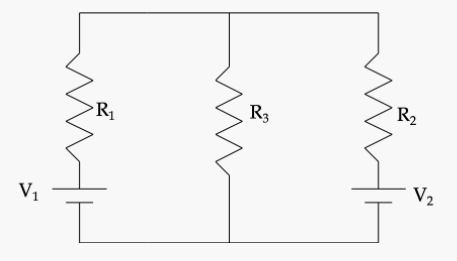
|
求圖中電路中每個電阻器的電流。 |
\begin{equation}
I_1=\dfrac{1}{22}\, \text{ A},\ I_2=\dfrac{6}{22}\, \text{ A},\ I_3=\dfrac{7}{22}\, \text{ A}.
\end{equation}
============Solution:=============
 |
\begin{equation} I_1 + I_2 - I_3 = 0.\label{eq-exp-kirk-two-source-three-loop-KCL} \end{equation} \begin{equation*} -I_3R_3 + V_1 - I_1R_1 = 0. \end{equation*} \begin{equation} -30 I_3 + 10 - 10 I_1 = 0.\label{eq-exp-kirk-two-source-three-loop-KVL-1} \end{equation} \begin{equation*} +I_2R_2 -V_2 + V_1 - I_1R_1 = 0. \end{equation*} \begin{equation} +20 I_2 -15 + 10 - 10 I_1 = 0.\label{eq-exp-kirk-two-source-three-loop-KVL-2} \end{equation} |
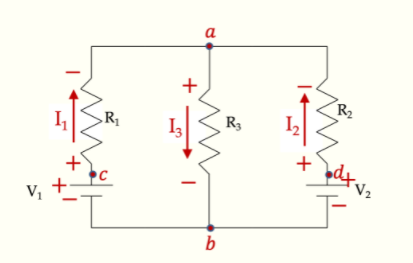
example
|
求圖中電路中每個電阻器的電流。 |
\(I = \dfrac{78}{155}\, \text{ A}\text{,} I_1 = \dfrac{51}{155}\, \text{ A}\text{,} I_2 = \dfrac{27}{155}\, \text{ A}\text{,} I_3 = \dfrac{45}{155}\, \text{ A}\text{,} I_4 = \dfrac{33}{155}\, \text{ A}\text{,} I_5 = \dfrac{6}{155}\, \text{ A}\text{,} \)
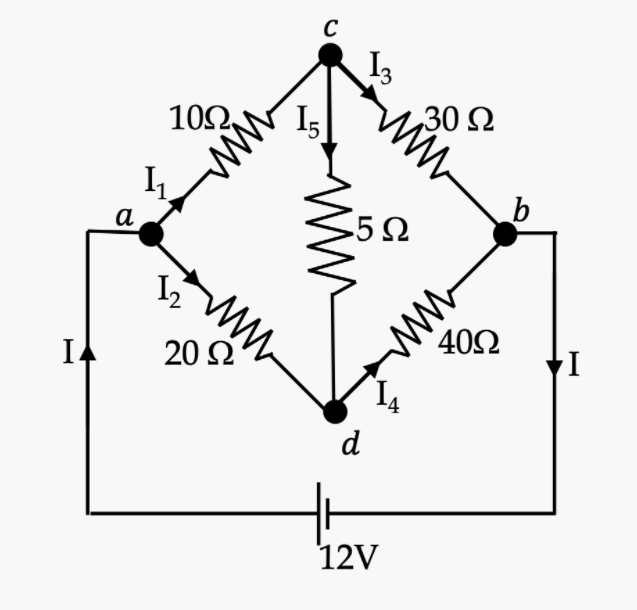
============Solution:=============
在這個由電阻所形成的一個電橋網路中,要求解流過每一個電阻的電流。首先我們注意到網路中總共有a,b,c,d四個節點,這四個節點有節點定理必須滿足。再其次,我們假設a,b,c,d個點的電位分別是\(\phi_a, \,\phi_b, \,\phi_c, \,\phi_d \),並且選擇電池的負端作為電位的0點,\(\phi_b=0\),因此a節點的電位\(\phi_a=12\) V。我們剩下\(\phi_c, \, \phi_d\)這兩個點的電位作為問題的變數。五個電阻的電流值可以歐姆定律,電流表示為電阻兩端的電位差除以該電阻的電阻值: \[I_1=\frac{12-\phi_c}{10};\quad I_2=\frac{12-\phi_d}{20};\quad I_3=\frac{\phi_c-0}{30};\quad I_4=\frac{\phi_d-0}{40};\quad I_5=\frac{\phi_c-\phi_d}{5} \] c,d的節點定理: \[I_1=I_3 + I_5, \quad I_4 = I_2 + I_5 \] 將每一個電阻的電流公式帶入上面兩個節點定理方程式可以得到\(\phi_c, \, \phi_d\)兩個變數的聯立方程式, \begin{align*} \amp 10 \phi_c - 6 \phi_d = 36,\\ \amp -8 \phi_c + 11 \phi_d = 24. \end{align*} 求解這兩個聯立方程式可以得到c和d兩點的電位分別如下: \begin{equation*} \phi_c = \dfrac{270}{31}\text{ V},\ \ \phi_d = \dfrac{264}{31}\text{ V}. \end{equation*} 再將這兩個電位帶入5個電阻電流的公式中,就可得到流過5個電阻的電流值:
\(I = \dfrac{78}{155}\, \text{ A}\text{,} I_1 = \dfrac{51}{155}\, \text{ A}\text{,} I_2 = \dfrac{27}{155}\, \text{ A}\text{,} I_3 = \dfrac{45}{155}\, \text{ A}\text{,} I_4 = \dfrac{33}{155}\, \text{ A}\text{,} I_5 = \dfrac{6}{155}\, \text{ A} \) 。
In a bridge circuit, resistors and other elements in a circuit form a bridge-like structure. You can analyze the circuit given in by setting up six equations for six currents. That is not the most economical way for analyzing this circuit since it has only four unique values of electic potentials at four nodes in the circuit. The values of potentials at two of the nodes is already known. Therefore, we need to find only two unknown potentials. Find values of electric potential at the four nodes in the circuit. Let \(\phi_a\text{,}\) \(\phi_b\text{,}\) \(\phi_c\text{,}\) and \(\phi_d\) denote electric potentials at \(a,\ b,\ c,\ d\) respectively. Since voltage source maintains potential difference across it, \begin{equation*} \phi_a - \phi_b = 12\text{ V}. \end{equation*} We can always, choose one place to be zero reference of electric potential. As customary, we will choose it to be the negative of a voltage source. Note, if we had multiple voltage sources, negative of only one of them can be set to zero. \begin{equation*} \phi_b = 0,\ \phi_a= 12\text{ V}. \end{equation*} From the circuit we have the following for Ohm's law for each resistor. \begin{align*} \amp 12- \phi_c = 10 I_1\\ \amp 12- \phi_d = 20 I_2\\ \amp \phi_c -0 = 30 I_3\\ \amp \phi_d -0 = 40 I_4\\ \amp \phi_c - \phi_d = 5 I_5 \end{align*} We will use these to replace currents in the following KCL equations at nodes \(c\) and \(d\text{,}\) \begin{align*} \amp I_1 = I_3 + I_5,\\ \amp I_4 = I_2 + I_5, \end{align*} which gives \begin{align*} \amp \dfrac{12-\phi_c}{10} = \dfrac{\phi_c}{30} + \dfrac{\phi_c - \phi_d}{5},\\ \amp \dfrac{ \phi_d}{40} = \dfrac{12-\phi_d}{20} + \dfrac{\phi_c - \phi_d}{5}. \end{align*} These can be simplified to \begin{align*} \amp 10 \phi_c - 6 \phi_d = 36,\\ \amp -8 \phi_c + 11 \phi_d = 24. \end{align*} Solving them yields \begin{equation*} \phi_c = \dfrac{270}{31}\text{ V},\ \ \phi_d = \dfrac{264}{31}\text{ V}. \end{equation*} From the potentials, it is trivial to get the currents now.
============Solution:=============
在這個由電阻所形成的一個電橋網路中,要求解流過每一個電阻的電流。首先我們注意到網路中總共有a,b,c,d四個節點,這四個節點有節點定理必須滿足。再其次,我們假設a,b,c,d個點的電位分別是\(\phi_a, \,\phi_b, \,\phi_c, \,\phi_d \),並且選擇電池的負端作為電位的0點,\(\phi_b=0\),因此a節點的電位\(\phi_a=12\) V。我們剩下\(\phi_c, \, \phi_d\)這兩個點的電位作為問題的變數。五個電阻的電流值可以歐姆定律,電流表示為電阻兩端的電位差除以該電阻的電阻值: \[I_1=\frac{12-\phi_c}{10};\quad I_2=\frac{12-\phi_d}{20};\quad I_3=\frac{\phi_c-0}{30};\quad I_4=\frac{\phi_d-0}{40};\quad I_5=\frac{\phi_c-\phi_d}{5} \] c,d的節點定理: \[I_1=I_3 + I_5, \quad I_4 = I_2 + I_5 \] 將每一個電阻的電流公式帶入上面兩個節點定理方程式可以得到\(\phi_c, \, \phi_d\)兩個變數的聯立方程式, \begin{align*} \amp 10 \phi_c - 6 \phi_d = 36,\\ \amp -8 \phi_c + 11 \phi_d = 24. \end{align*} 求解這兩個聯立方程式可以得到c和d兩點的電位分別如下: \begin{equation*} \phi_c = \dfrac{270}{31}\text{ V},\ \ \phi_d = \dfrac{264}{31}\text{ V}. \end{equation*} 再將這兩個電位帶入5個電阻電流的公式中,就可得到流過5個電阻的電流值:
\(I = \dfrac{78}{155}\, \text{ A}\text{,} I_1 = \dfrac{51}{155}\, \text{ A}\text{,} I_2 = \dfrac{27}{155}\, \text{ A}\text{,} I_3 = \dfrac{45}{155}\, \text{ A}\text{,} I_4 = \dfrac{33}{155}\, \text{ A}\text{,} I_5 = \dfrac{6}{155}\, \text{ A} \) 。
In a bridge circuit, resistors and other elements in a circuit form a bridge-like structure. You can analyze the circuit given in by setting up six equations for six currents. That is not the most economical way for analyzing this circuit since it has only four unique values of electic potentials at four nodes in the circuit. The values of potentials at two of the nodes is already known. Therefore, we need to find only two unknown potentials. Find values of electric potential at the four nodes in the circuit. Let \(\phi_a\text{,}\) \(\phi_b\text{,}\) \(\phi_c\text{,}\) and \(\phi_d\) denote electric potentials at \(a,\ b,\ c,\ d\) respectively. Since voltage source maintains potential difference across it, \begin{equation*} \phi_a - \phi_b = 12\text{ V}. \end{equation*} We can always, choose one place to be zero reference of electric potential. As customary, we will choose it to be the negative of a voltage source. Note, if we had multiple voltage sources, negative of only one of them can be set to zero. \begin{equation*} \phi_b = 0,\ \phi_a= 12\text{ V}. \end{equation*} From the circuit we have the following for Ohm's law for each resistor. \begin{align*} \amp 12- \phi_c = 10 I_1\\ \amp 12- \phi_d = 20 I_2\\ \amp \phi_c -0 = 30 I_3\\ \amp \phi_d -0 = 40 I_4\\ \amp \phi_c - \phi_d = 5 I_5 \end{align*} We will use these to replace currents in the following KCL equations at nodes \(c\) and \(d\text{,}\) \begin{align*} \amp I_1 = I_3 + I_5,\\ \amp I_4 = I_2 + I_5, \end{align*} which gives \begin{align*} \amp \dfrac{12-\phi_c}{10} = \dfrac{\phi_c}{30} + \dfrac{\phi_c - \phi_d}{5},\\ \amp \dfrac{ \phi_d}{40} = \dfrac{12-\phi_d}{20} + \dfrac{\phi_c - \phi_d}{5}. \end{align*} These can be simplified to \begin{align*} \amp 10 \phi_c - 6 \phi_d = 36,\\ \amp -8 \phi_c + 11 \phi_d = 24. \end{align*} Solving them yields \begin{equation*} \phi_c = \dfrac{270}{31}\text{ V},\ \ \phi_d = \dfrac{264}{31}\text{ V}. \end{equation*} From the potentials, it is trivial to get the currents now.
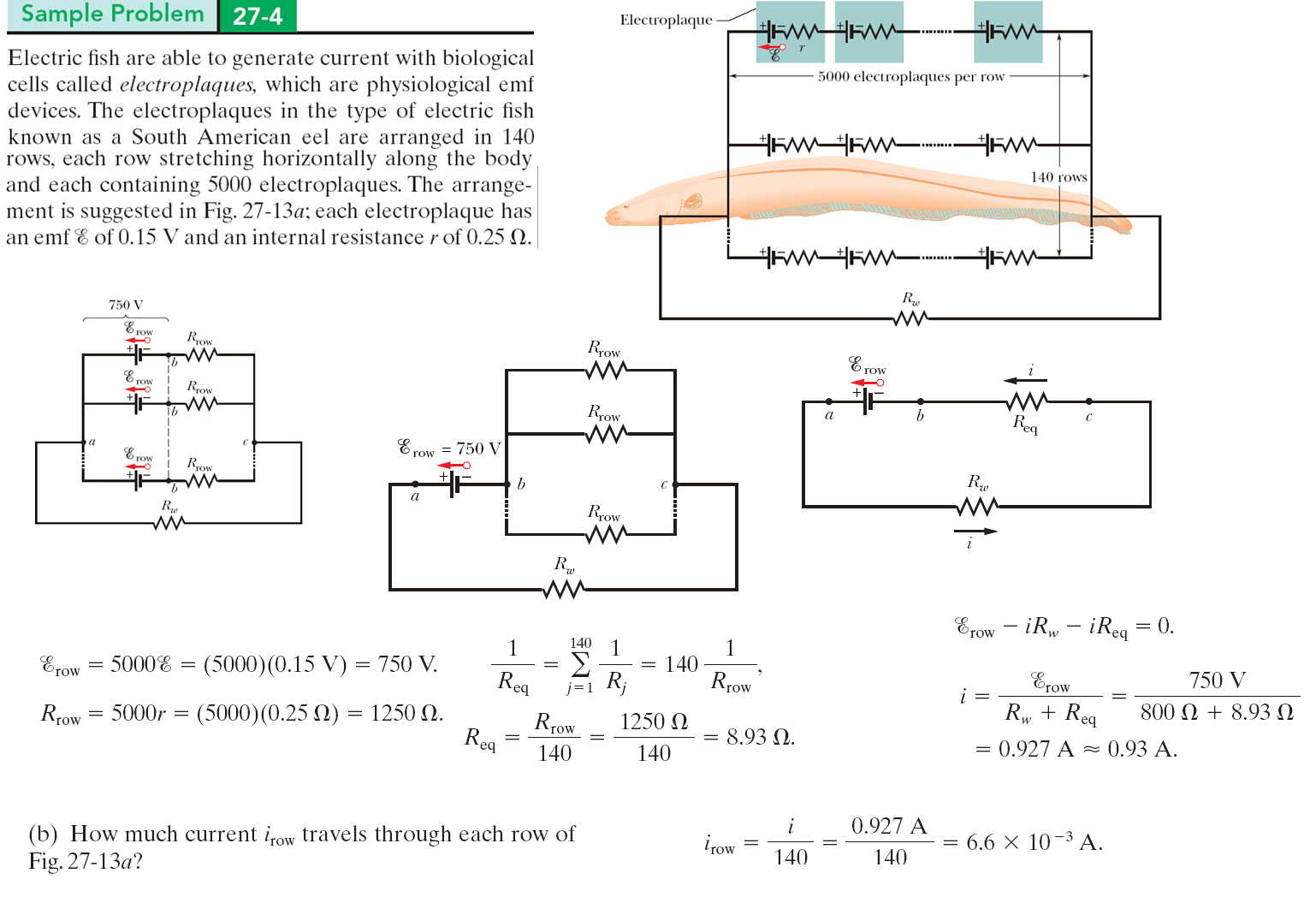
範例-4:電魚的電流迴路
|
電魚能夠利用稱為電板的生物細胞產生電流,電板是一種生理電動勢裝置。 被稱為南美鰻魚的電魚類型的電板排列成 140 排,每排沿身體水平延伸,每排包含 5000 個電板。 安排如圖所示; 每個電板都有一個電動勢 \(\mathscr{E}= 0.15\) V 和一個內阻 \(r= 0.25\,\Omega\)。 鰻魚周圍的水在電板陣列的兩端之間形成一個迴路,一端在動物的頭部,另一端靠近尾巴。 (a) 如果鰻魚周圍的水有電阻\(R_{water}= 800 \,\Omega\),鰻魚在水中能產生多少電流? (b) 多少電流\(i_{row}\) 穿過右圖的每一行? |
|
RC-電路
充了電的電容器可以作為一個可攜式的電荷供應器。當我們將一個充電的電容器用一個導線將兩個平板接通的時候,帶負電荷電板上的電子將會流向另外一面導體電板,造成所謂電容的放電現象。因此在電容的應用中充電與放電是非常基本的兩個過程,在這個小單元當中我們將要進行電容電阻充放電相關的計算。電容放電網路
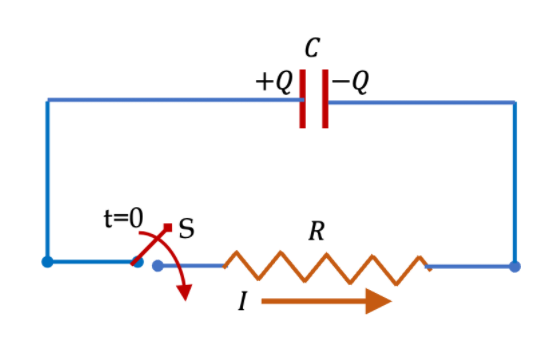 假設我們已經有一個充了電的電容器如圖所示,若要使用充電電容器上的電荷,可以通過電阻 \(R\) 的裝置和開關 \(S\) 連接電容器的末端,如圖所示。當開關閉合時,電流在電路中流動,直到來自負極板的電子中和正極板上的正電荷。放電速率取決於板上電荷的當前值,這導致電荷呈指數衰減。令 \(Q_0\) 為 \(t = 0\) 時的起始電荷。然後,使用微分方程我們可以推導出電容上的電荷量隨著時間變化的函數關係\(Q(t)\),我們在下面會推導,在此先把最後的指數函數呈現如下:
\begin{equation*}
Q(t) = Q_0 e^{ - t/RC}.
\end{equation*}
而相對應的圖形如右圖所示。
假設我們已經有一個充了電的電容器如圖所示,若要使用充電電容器上的電荷,可以通過電阻 \(R\) 的裝置和開關 \(S\) 連接電容器的末端,如圖所示。當開關閉合時,電流在電路中流動,直到來自負極板的電子中和正極板上的正電荷。放電速率取決於板上電荷的當前值,這導致電荷呈指數衰減。令 \(Q_0\) 為 \(t = 0\) 時的起始電荷。然後,使用微分方程我們可以推導出電容上的電荷量隨著時間變化的函數關係\(Q(t)\),我們在下面會推導,在此先把最後的指數函數呈現如下:
\begin{equation*}
Q(t) = Q_0 e^{ - t/RC}.
\end{equation*}
而相對應的圖形如右圖所示。
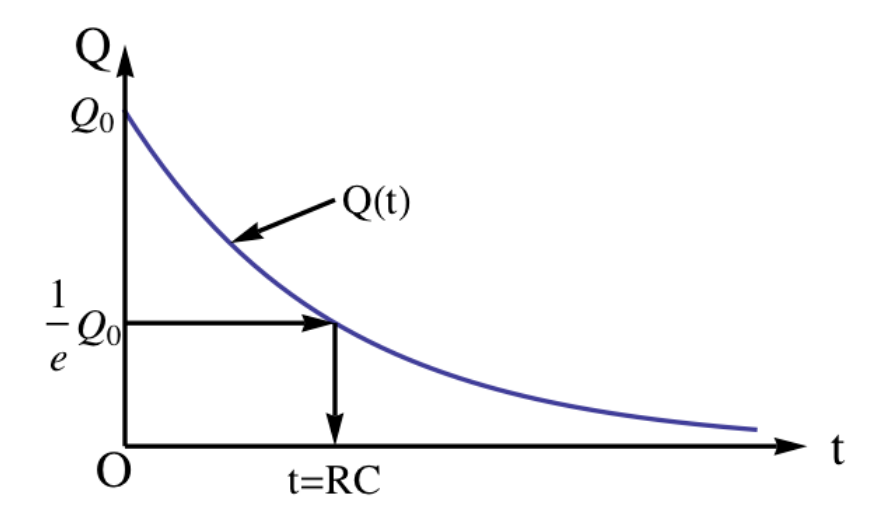 電容放電的速率就是電容上的電荷量對時間的微分(\(-\dfrac{dQ}{dt}=i\))也就是放電的電流其公式如下:
\[i=-\dfrac{dQ}{dt}=\dfrac{Q}{RC}=\dfrac{Q}{\tau}\]
電路中的電流隨時間變化,並且與瞬間板上的電荷成正比。達到原始電荷的 \(1/e\) 的時間(\(\tau=RC\)),其中 \(e\) 是歐拉數,值 \(e = 2.718...\),是電路的一個重要特徵。這個時間稱為電路的時間常數。時間常數通常用希臘字母\(\tau\)表示。當然,在這段時間內,大約\(2/3\)的電荷已經通過電路放電。電路的時間常數是電路的電阻和電容的乘積:\(\tau=RC\)。通過調整 \(R\),我們可以控制電容器放電的速率。下面我們將研究充電過程,我們會在那裡發現充電速率也具有相同的時間常數\(RC\)。
電容放電的速率就是電容上的電荷量對時間的微分(\(-\dfrac{dQ}{dt}=i\))也就是放電的電流其公式如下:
\[i=-\dfrac{dQ}{dt}=\dfrac{Q}{RC}=\dfrac{Q}{\tau}\]
電路中的電流隨時間變化,並且與瞬間板上的電荷成正比。達到原始電荷的 \(1/e\) 的時間(\(\tau=RC\)),其中 \(e\) 是歐拉數,值 \(e = 2.718...\),是電路的一個重要特徵。這個時間稱為電路的時間常數。時間常數通常用希臘字母\(\tau\)表示。當然,在這段時間內,大約\(2/3\)的電荷已經通過電路放電。電路的時間常數是電路的電阻和電容的乘積:\(\tau=RC\)。通過調整 \(R\),我們可以控制電容器放電的速率。下面我們將研究充電過程,我們會在那裡發現充電速率也具有相同的時間常數\(RC\)。下面我們透過電路的迴路定理來寫出電容放電網路的微分方程,並且找出微分方程的解。上圖的電路中我們可以看見,當開關接上了以後會有電流從電容一端發出流過電阻,到達電容平行板的另外一端,迴路定理告訴我們,電容上的電位差必然等於電阻兩端的電位差,也就是下面這個公式: \begin{equation} -R I + V_c = 0.\label{eq-cap-discharging-circuit-KVL-loop-eq} \end{equation} 電容上的電位差滿足\(V_c(t) = \dfrac{Q(t)}{C}\)這個關係,並且電流又與電荷放電的速率有關:\(I = - \dfrac{dQ}{dt}\),因此上面的公式又可寫成 \begin{equation} \dfrac{dQ}{dt} = - \dfrac{1}{RC}\,Q \end{equation} 上面這個微分方程式可以很容易的證明,下面所呈現的指數函數滿足微分方程,因此它是一個解: \begin{equation} Q(t) = Q_0\, e^{- t / RC}. \end{equation} 為了滿足初始的條件,\(Q_0\)也就是時間t=0的時候平行板電容上面的電荷量\(Q(0)=Q_0\)。基本上這個就是電容放電網路的解,同時我們可以利用微分關係寫下電容放電時電流對時間的函數關係,以及平行板電容上的電位差隨時間的變化函數: \begin{align*} I \amp = -\dfrac{dQ}{dt} = \dfrac{Q_0}{RC}\, e^{- t / RC}.\\ V_c \amp = \dfrac{Q}{C} = \dfrac{Q_0}{C}\, e^{- t / RC}. \end{align*}
電容充電網路
為了給電容器充電,我們使用恆定電動勢emf源,如圖所示的電路。在圖中,電容為 \(C\) 的電容器與電壓為 \(V\) 的emf源串聯。電阻\(R\)是電路中的總電阻,並且包括一個開關\(S\)來控制電路的閉合和斷開。假設電容器在時間 \(t = 0\) 時未充電。當開關 \(S\) 閉合時,emf源在電路中建立一個電場,使電子在導線中流動。然而,當電子到達電容器的負極板時,它們不能移動到正極板,因為極板之間有絕緣體。相反,負極板上的電子積聚會排斥正極板上的電子。隨著電荷在電容器上的積累,電容器上的電荷電場完全抵消了emf源的電場,從而使電流結束流動。電容器變為開路,電源的所有電壓 V 都下降到電容器上。我們說電容器已充滿電,電荷 \(Q = C V\)。通過使用迴路定理並求解該方程,我們在下面顯示了初始未充電電容器上瞬間 \(t\) 的電荷由 \[Q ( t) = C V [ 1 - \exp (- t / R C) ]\] 隨著 \(t \rightarrow \infty\) ,第二項變為零。也就是說,當電容器充滿電時,電容器上的最終電荷將為 \(Q_{\text{final}} = C V\)。 這證實了最終,emf源的所有電壓都下降到電容器上。函數 \(Q ( t)\) 還表明電荷達到 \( 1 - 1/e \) 需要時間 \(\tau=RC\),即大約是2/3的最終值,與我們獲得的電容器放電時間相同。我們把這個時間當作充電所需要的時間,也是放電所需要的時間,是一個特徵時間,在時間\(\tau\)內,電容器“充分”充電。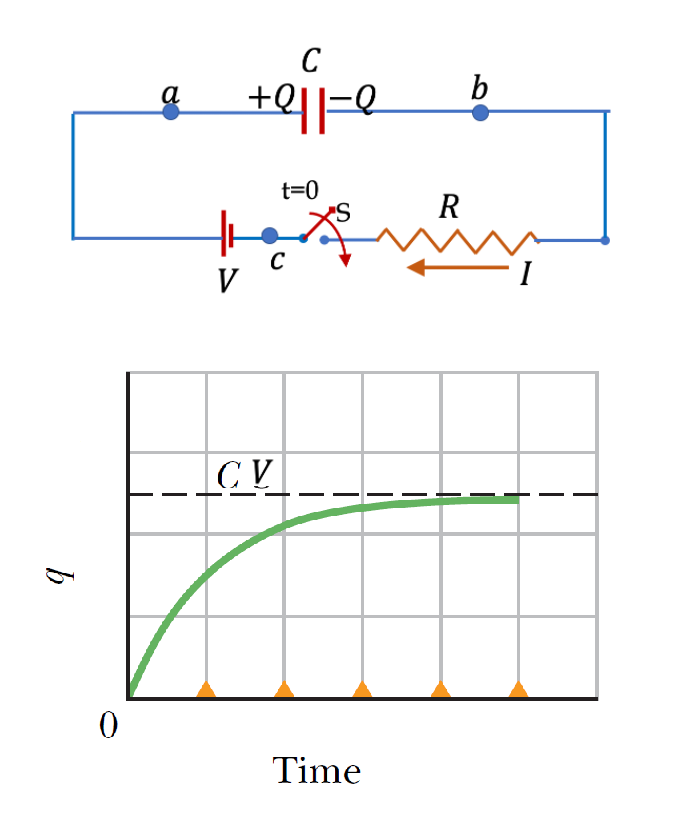
下面我們利用迴路定理來寫出,電容充電的微分方程式和這個方程式的解。
考慮某一時刻的電路狀態 \(t\text{.}\) 令 \(\pm Q(t)\) 為電容器上的電荷,我們希望確定其公式。令 \(I(t)\) 為此時電路中的電流。電容器兩端的電壓降 \(V_c\) 將由電容器公式給出, \begin{equation*} V_c = \dfrac{Q}{C} \end{equation*} 現在,在循環 \(a-b-c-a\text{,}\) 中應用迴路定理規則,我們將得到 \begin{equation*} -V_c - R I + V = 0。 \end{equation*} 當電流流入電容器的正極板時,該板上的電荷 \(Q\) 會增加。因此,我們將有 \begin{equation*} I = \dfrac{dQ}{dt} \end{equation*} 從上面的三個方程中,我們得到了以下關於電荷積累率的方程: \begin{equation*} \dfrac{dQ}{dt} + \dfrac{Q}{RC} = \dfrac{V}{R}. \end{equation*} 假設我們從未充電的電容器開始\(Q(0) = 0\text{.}\) ,尋求這個方程的解。要直接從微分方程式求解,需要一些時間學習微分方程求解的數學基礎,但是我們可以透過將已知的函數微分,來證實選取的函數確實是微分方程的解。首先我們提出一個指數成長函數作為上面的微分方程的解: \begin{equation*} Q(t) = CV \left[ 1- \exp{\left(-t/RC\right)} \right]. \end{equation*}
我們怎樣才能得到這個答案?讓我們先定義一個新的變量\(f\):
\begin{equation*}
f(t) = Q(t) - CV,
\end{equation*}
然後,我們會得到
\begin{equation*}
\dfrac{df}{dt} = \dfrac{dQ}{dt} - 0,,
\end{equation*}
可以使用方程式進行轉換。
\begin{align*}
\dfrac{df}{dt} \amp = - \dfrac{Q}{RC} + \dfrac{V}{R}, \\
\amp = - \dfrac{f + CV}{RC} + \dfrac{V}{R},\\
\amp = - \dfrac{f}{RC}。
\end{align*}
即 \(f(t)\) 服從一個更簡單的方程,
\[\dfrac{df}{dt} = - \dfrac{1}{RC}\, f,\]
這是我們在放電電路中遇到的方程。這個方程的解很容易寫下來。
\[f(t) = f(0)\, \exp\left(- \dfrac{t}{RC} \right)。\]
因此,\(Q(t)\) 是
\begin{align*}
Q(t)\amp = f(t) + CV \\
\amp = f(0)\, \exp\left(- \dfrac{t}{RC} \right) + CV。
\end{align*}
現在,我們使用初始條件在 \(t=0\text{,} Q=0\text{.}\) 這個條件可以給我們對應的初始條件 \(f(0)\text{.}\)
\[0 = f(0)\times 1 + CV\Longrightarrow f(0) = - CV。\]
所以,
\[Q(t) = -CV\, \exp\left(- \dfrac{t}{RC} \right) + CV。\]
這是方程式中的答案。
從 \(Q(t)\) 我們可以通過對 \(Q(t)\text{.}\) 求導數得到電流:
\[I(t) = \dfrac{dQ}{dt} = \dfrac{V}{R}\, \exp\left(- \dfrac{t}{RC} \right)\]
它表明最大電流 \(I_\text{max} = V/R\text{,}\) 位於 \(t=0\text{.}\) 這對應於 emf 的所有電壓下降到電阻和電容周圍沒有。這是有道理的,因為此時電容器沒有電荷,因此沒有電壓降。隨著時間的流逝,電流隨著時間常數 \(\tau = RC\text{ }\) 漸漸消失。
HL示例問題:RC網路-1
YN示例問題:RC網路-2
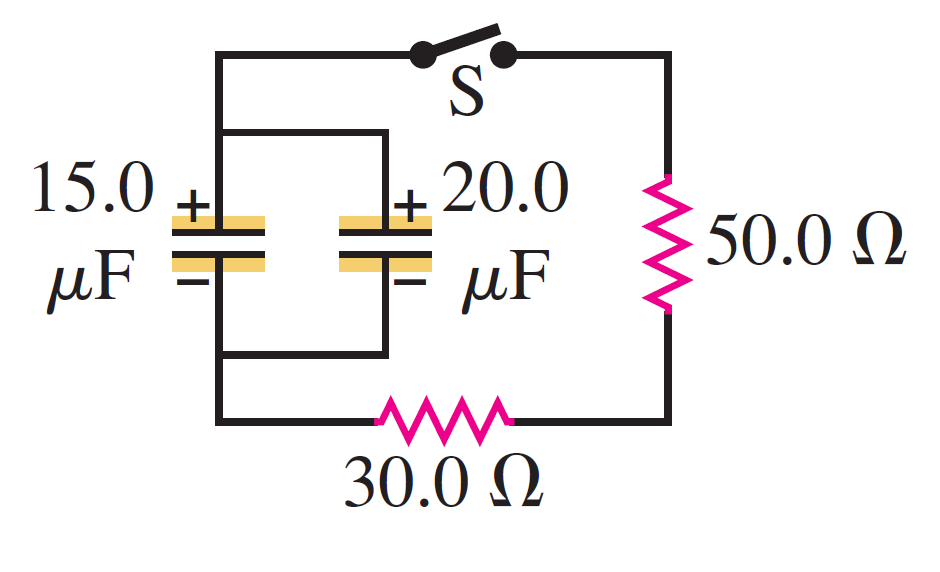 在這個電阻和電容的網路當中並沒有電池,但是起初的時候兩個並聯的電容上面都有電荷,電容上的電位差都是45伏特。在時間\(t=0\)的時候將開關接上,電容上的電荷開始放電。要我們計算電容上的電位差下降到10伏特,需要經過多久的時間,並且計算在這個時刻流過電阻的電流。
在這個電阻和電容的網路當中並沒有電池,但是起初的時候兩個並聯的電容上面都有電荷,電容上的電位差都是45伏特。在時間\(t=0\)的時候將開關接上,電容上的電荷開始放電。要我們計算電容上的電位差下降到10伏特,需要經過多久的時間,並且計算在這個時刻流過電阻的電流。這個問題的考慮非常簡單,隨著電荷從電容上流失,電容上的電位差就會下降,而流失的電荷流經過兩個串聯的電阻,會形成流過電阻的電流。兩個電阻串聯可以用一個等效電阻取代,兩個並聯的電容也可以用一個等效電容取代。等效電容是兩個分電容的和,等效電阻也是兩個分電阻的和。因此整個網路等效於一個只有單一一個電阻和電容的放電網路。因此電位差和電流都是指數衰減函數,而其中的時間常數,可以從等效電容值和等效電阻值得到: \[R_s=R_1 + R_2=80 \,\Omega; \quad C_p=C_1 + C_2=35 \, \mu F\] \[V_C(t)=V_0 e^{-t/\tau}; \quad V_0=45; \,\, \tau=R_s C_p=2.8 \times 10^{-3} \, s\] \[I(t)=\dfrac{V_0}{R_s} e^{-t/\tau}\] \[10=45 e^{-t/(2.8 \times 10^{-3})}; \Rightarrow t=(-2.8 \times 10^{-3})(\ln \dfrac{10}{45})=4.21 \times 10^{-3} \, s\]
HL27示例問題-5:汽車RC放電
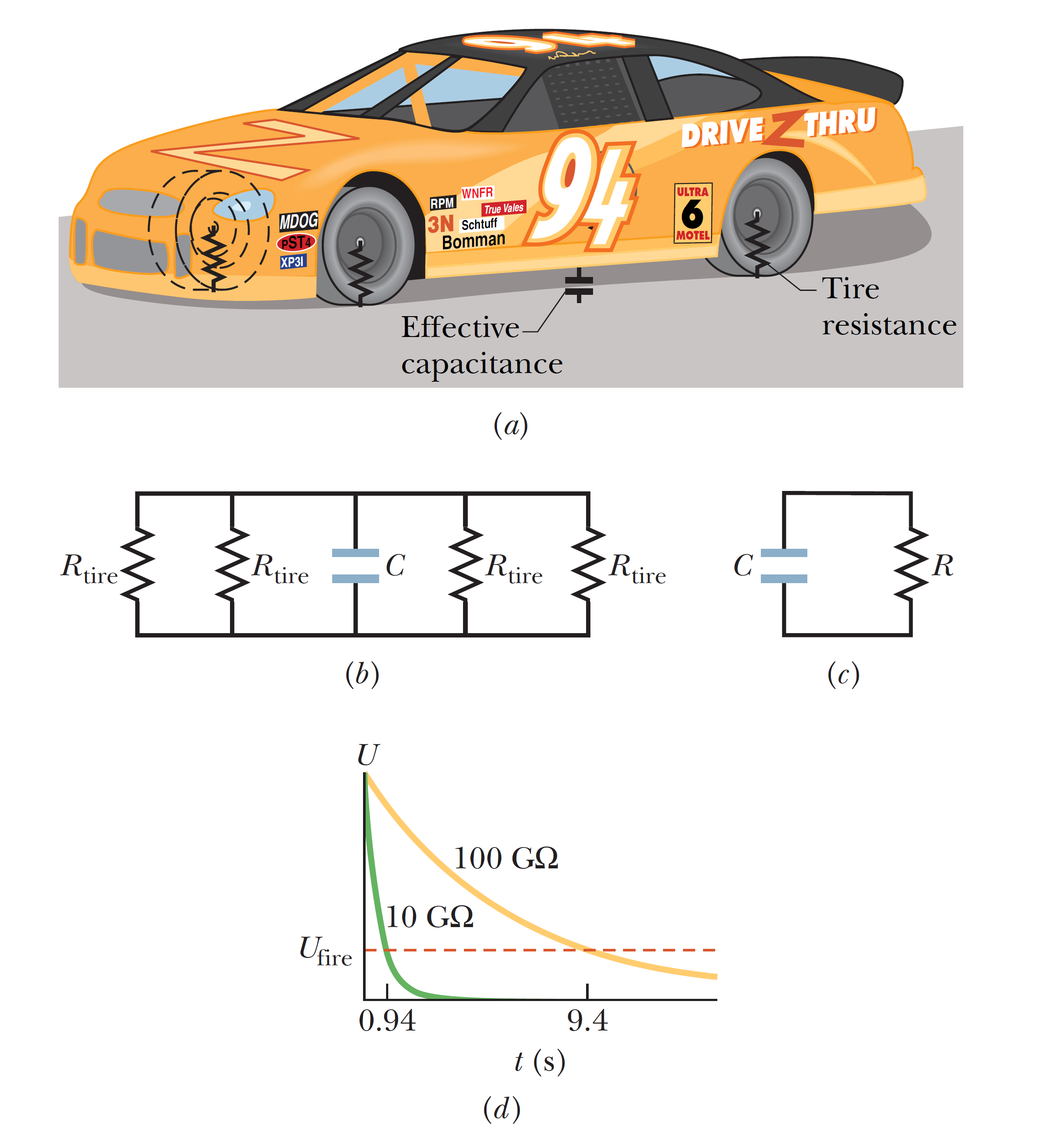 As a car rolls along pavement, electrons move from the pavement first onto the tires and then onto the car body. The car stores this excess charge and the associated electric potential energy as if the car body were one plate of a capacitor and the pavement were the other plate. When the car stops, it discharges its excess charge and energy through the tires, just as a capacitor can discharge through a resistor. If a conducting object comes within a few centimeters of the car before the car is discharged, the remaining energy can be suddenly transferred to a spark between the car and the object. Suppose the conducting object is a fuel dispenser. The spark will not ignite the fuel and cause a fire if the spark energy is less than the critical value \(U_{fire}=50\) mJ. When the car of the figure stops at time \(t = 0\), the car-ground potential difference is \(V_0 = 30\) kV. The car-ground capacitance is \(C= 500\) pF, and the resistance of each tire is \(R_{tire}=100\) G\(\Omega\). How much time does the car take to discharge through the tires to drop below the critical value \(U_{fire}\)?
As a car rolls along pavement, electrons move from the pavement first onto the tires and then onto the car body. The car stores this excess charge and the associated electric potential energy as if the car body were one plate of a capacitor and the pavement were the other plate. When the car stops, it discharges its excess charge and energy through the tires, just as a capacitor can discharge through a resistor. If a conducting object comes within a few centimeters of the car before the car is discharged, the remaining energy can be suddenly transferred to a spark between the car and the object. Suppose the conducting object is a fuel dispenser. The spark will not ignite the fuel and cause a fire if the spark energy is less than the critical value \(U_{fire}=50\) mJ. When the car of the figure stops at time \(t = 0\), the car-ground potential difference is \(V_0 = 30\) kV. The car-ground capacitance is \(C= 500\) pF, and the resistance of each tire is \(R_{tire}=100\) G\(\Omega\). How much time does the car take to discharge through the tires to drop below the critical value \(U_{fire}\)? 當汽車在人行道上行駛時,電子首先從人行道移動到輪胎上,然後再到車身上。汽車存儲這種多餘的電荷和相關的電勢能,就好像車身是電容器的一個板,而路面是另一個板。當汽車停下來時,它會通過輪胎釋放多餘的電荷和能量,就像電容器可以通過電阻器放電一樣。如果一個導電物體在汽車放電前進入汽車幾厘米內,剩餘的能量會突然轉移到汽車和物體之間的火花上。假設導電物體是加油機。如果火花能量小於臨界值 \(U_{fire}=50\) mJ,火花將不會點燃燃料並引起火災。當圖中的汽車在時間 \(t = 0\) 停車時,汽車與地之間的電位差為 \(V_0 = 30\) kV。汽車對地電容為\(C= 500\) pF,每個輪胎的電阻為\(R_{tire}=100\) G\(\Omega\)。汽車需要多長時間才能通過輪胎排放到臨界值 \(U_{fire}\) 以下?
\[\dfrac{1}{R}=\dfrac{1}{R_{tire}}+\dfrac{1}{R_{tire}}+\dfrac{1}{R_{tire}}+\dfrac{1}{R_{tire}}\] \[R=\dfrac{R_{tire}}{4}=\dfrac{100 \times 10^9}{4}=25 \times 10^9 \,\Omega\] \[U=\dfrac{q^2}{2C}=\dfrac{1}{2C} \left( q_0 e^{-\frac{t}{RC}} \right)^2 \] \[U=\dfrac{q_0^2}{2C} e^{-\frac{2t}{RC}} \] \[q=CV; \quad q_0=CV_0 \Rightarrow U=\dfrac{(CV_0)^2}{2C} e^{-\frac{2t}{RC}}=\dfrac{V_0^2}{2} e^{-\frac{2t}{RC}} \] \[e^{-\frac{2t}{RC}=\dfrac{2U}{(CV_0)^2}}.\] \[-\dfrac{2t}{RC}=\ln \left( \dfrac{2U}{CV_0^2} \right),\] \[t=-\dfrac{RC}{2} \ln \left( \dfrac{2U}{CV_0^2} \right),\] \[t=-\dfrac{(25\times 10^9)(500 \times 10^{-12}}{2} \ln \left( \dfrac{2(50 \times 10^{-3}}{(500 \times 10^{-12})(30\times 10^3)^2} \right)=9.4 \,\text{s}\]
授課教師
陳永忠 ycchen@thu.edu.tw