RC-電路
充了電的電容器可以作為一個可攜式的電荷供應器。當我們將一個充電的電容器用一個導線將兩個平板接通的時候，帶負電荷電板上的電子將會流向另外一面導體電板，造成所謂電容的放電現象。因此在電容的應用中充電與放電是非常基本的兩個過程，在這個小單元當中我們將要進行電容電阻充放電相關的計算。電容放電網路
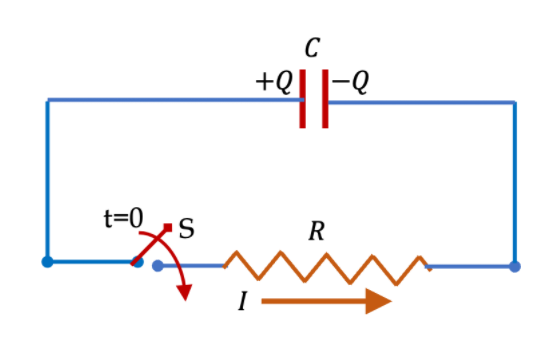假設我們已經有一個充了電的電容器如圖所示，若要使用充電電容器上的電荷，可以通過電阻 \(R\) 的裝置和開關 \(S\) 連接電容器的末端，如圖所示。當開關閉合時，電流在電路中流動，直到來自負極板的電子中和正極板上的正電荷。放電速率取決於板上電荷的當前值，這導致電荷呈指數衰減。令 \(Q_0\) 為 \(t = 0\) 時的起始電荷。然後，使用微分方程我們可以推導出電容上的電荷量隨著時間變化的函數關係\(Q(t)\)，我們在下面會推導，在此先把最後的指數函數呈現如下：
\begin{equation*}
Q(t) = Q_0 e^{ - t/RC}.
\end{equation*}
而相對應的圖形如右圖所示。
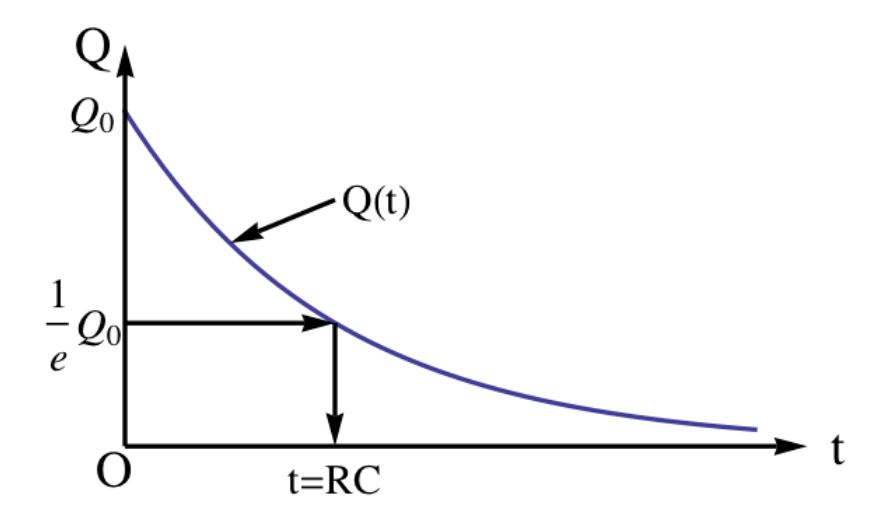電容放電的速率就是電容上的電荷量對時間的微分(\(-\dfrac{dQ}{dt}=i\))也就是放電的電流其公式如下：
\[i=-\dfrac{dQ}{dt}=\dfrac{Q}{RC}=\dfrac{Q}{\tau}\]
電路中的電流隨時間變化，並且與瞬間板上的電荷成正比。達到原始電荷的 \(1/e\) 的時間(\(\tau=RC\))，其中 \(e\) 是歐拉數，值 \(e = 2.718...\)，是電路的一個重要特徵。這個時間稱為電路的時間常數。時間常數通常用希臘字母\(\tau\)表示。當然，在這段時間內，大約\(2/3\)的電荷已經通過電路放電。電路的時間常數是電路的電阻和電容的乘積：\(\tau=RC\)。通過調整 \(R\)，我們可以控制電容器放電的速率。下面我們將研究充電過程，我們會在那裡發現充電速率也具有相同的時間常數\(RC\)。下面我們透過電路的迴路定理來寫出電容放電網路的微分方程，並且找出微分方程的解。上圖的電路中我們可以看見，當開關接上了以後會有電流從電容一端發出流過電阻，到達電容平行板的另外一端，迴路定理告訴我們，電容上的電位差必然等於電阻兩端的電位差，也就是下面這個公式： \begin{equation} -R I + V_c = 0.\label{eq-cap-discharging-circuit-KVL-loop-eq}\tag{37.1.3} \end{equation} 電容上的電位差滿足\(V_c(t) = \dfrac{Q(t)}{C}\)這個關係，並且電流又與電荷放電的速率有關：\(I = - \dfrac{dQ}{dt}\)，因此上面的公式又可寫成 \begin{equation} \dfrac{dQ}{dt} = - \dfrac{1}{RC}\,Q \end{equation} 上面這個微分方程式可以很容易的證明，下面所呈現的指數函數滿足微分方程，因此它是一個解： \begin{equation} Q(t) = Q_0\, e^{- t / RC}. \end{equation} 為了滿足初始的條件，\(Q_0\)也就是時間t=0的時候平行板電容上面的電荷量\(Q(0)=Q_0\)。基本上這個就是電容放電網路的解，同時我們可以利用微分關係寫下電容放電時電流對時間的函數關係，以及平行板電容上的電位差隨時間的變化函數： \begin{align*} I \amp = -\dfrac{dQ}{dt} = \dfrac{Q_0}{RC}\, e^{- t / RC}.\\ V_c \amp = \dfrac{Q}{C} = \dfrac{Q_0}{C}\, e^{- t / RC}. \end{align*}
電容充電網路
為了給電容器充電，我們使用恆定電動勢emf源，如圖所示的電路。在圖中，電容為 \(C\) 的電容器與電壓為 \(V\) 的emf源串聯。電阻\(R\)是電路中的總電阻，並且包括一個開關\(S\)來控制電路的閉合和斷開。假設電容器在時間 \(t = 0\) 時未充電。當開關 \(S\) 閉合時，emf源在電路中建立一個電場，使電子在導線中流動。然而，當電子到達電容器的負極板時，它們不能移動到正極板，因為極板之間有絕緣體。相反，負極板上的電子積聚會排斥正極板上的電子。隨著電荷在電容器上的積累，電容器上的電荷電場完全抵消了emf源的電場，從而使電流結束流動。電容器變為開路，電源的所有電壓 V 都下降到電容器上。我們說電容器已充滿電，電荷 \(Q = C V\)。通過使用迴路定理並求解該方程，我們在下面顯示了初始未充電電容器上瞬間 \(t\) 的電荷由 \[Q ( t) = C V [ 1 - \exp (- t / R C) ]\] 隨著 \(t \rightarrow \infty\) ，第二項變為零。也就是說，當電容器充滿電時，電容器上的最終電荷將為 \(Q_{\text{final}} = C V\)。 這證實了最終，emf源的所有電壓都下降到電容器上。函數 \(Q ( t)\) 還表明電荷達到 \( 1 - 1/e \) 需要時間 \(\tau=RC\)，即大約是2/3的最終值，與我們獲得的電容器放電時間相同。我們把這個時間當作充電所需要的時間，也是放電所需要的時間，是一個特徵時間，在時間\(\tau\)內，電容器“充分”充電。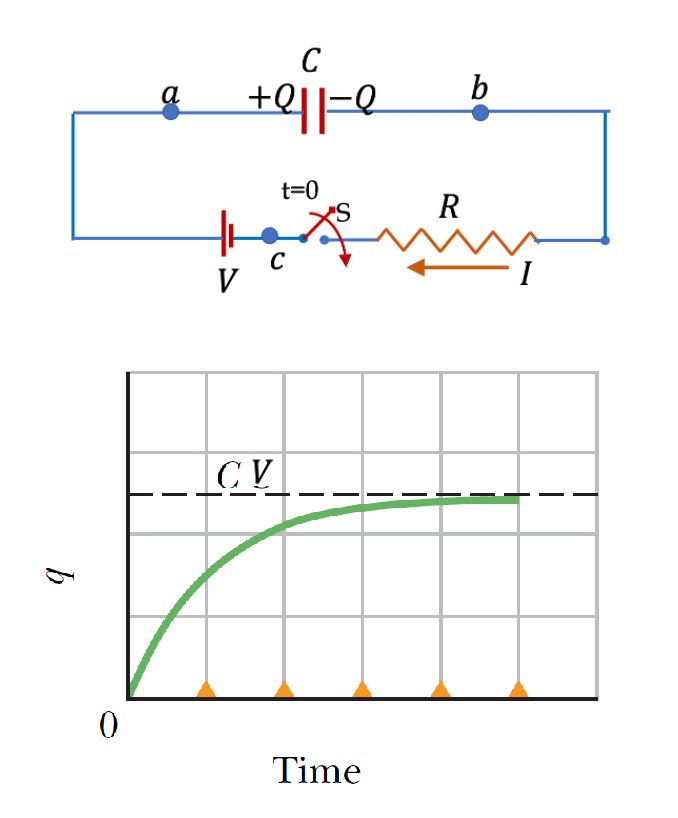
下面我們利用迴路定理來寫出，電容充電的微分方程式和這個方程式的解。
考慮某一時刻的電路狀態 \(t\text{.}\) 令 \(\pm Q(t)\) 為電容器上的電荷，我們希望確定其公式。令 \(I(t)\) 為此時電路中的電流。電容器兩端的電壓降 \(V_c\) 將由電容器公式給出， \begin{equation*} V_c = \dfrac{Q}{C} \end{equation*} 現在，在循環 \(a-b-c-a\text{,}\) 中應用迴路定理規則，我們將得到 \begin{equation*} -V_c - R I + V = 0。 \end{equation*} 當電流流入電容器的正極板時，該板上的電荷 \(Q\) 會增加。因此，我們將有 \begin{equation*} I = \dfrac{dQ}{dt} \end{equation*} 從上面的三個方程中，我們得到了以下關於電荷積累率的方程： \begin{equation*} \dfrac{dQ}{dt} + \dfrac{Q}{RC} = \dfrac{V}{R}. \end{equation*} 假設我們從未充電的電容器開始\(Q(0) = 0\text{.}\) ，尋求這個方程的解。要直接從微分方程式求解，需要一些時間學習微分方程求解的數學基礎，但是我們可以透過將已知的函數微分，來證實選取的函數確實是微分方程的解。首先我們提出一個指數成長函數作為上面的微分方程的解： \begin{equation*} Q(t) = CV \left[ 1- \exp{\left(-t/RC\right)} \right]. \end{equation*}
我們怎樣才能得到這個答案？讓我們先定義一個新的變量\(f\)：
\begin{equation*}
f(t) = Q(t) - CV，
\end{equation*}
然後，我們會得到
\begin{equation*}
\dfrac{df}{dt} = \dfrac{dQ}{dt} - 0,,
\end{equation*}
可以使用方程式進行轉換。
\begin{align*}
\dfrac{df}{dt} \amp = - \dfrac{Q}{RC} + \dfrac{V}{R}, \\
\amp = - \dfrac{f + CV}{RC} + \dfrac{V}{R},\\
\amp = - \dfrac{f}{RC}。
\end{align*}
即 \(f(t)\) 服從一個更簡單的方程，
\[\dfrac{df}{dt} = - \dfrac{1}{RC}\, f,\]
這是我們在放電電路中遇到的方程。這個方程的解很容易寫下來。
\[f(t) = f(0)\, \exp\left(- \dfrac{t}{RC} \right)。\]
因此，\(Q(t)\) 是
\begin{align*}
Q(t)\amp = f(t) + CV \\
\amp = f(0)\, \exp\left(- \dfrac{t}{RC} \right) + CV。
\end{align*}
現在，我們使用初始條件在 \(t=0\text{,} Q=0\text{.}\) 這個條件可以給我們對應的初始條件 \(f(0)\text{.}\)
\[0 = f(0)\times 1 + CV\Longrightarrow f(0) = - CV。\]
所以，
\[Q(t) = -CV\, \exp\left(- \dfrac{t}{RC} \right) + CV。\]
這是方程式中的答案。
從 \(Q(t)\) 我們可以通過對 \(Q(t)\text{.}\) 求導數得到電流：
\[I(t) = \dfrac{dQ}{dt} = \dfrac{V}{R}\, \exp\left(- \dfrac{t}{RC} \right)\]
它表明最大電流 \(I_\text{max} = V/R\text{,}\) 位於 \(t=0\text{.}\) 這對應於 emf 的所有電壓下降到電阻和電容周圍沒有。這是有道理的，因為此時電容器沒有電荷，因此沒有電壓降。隨著時間的流逝，電流隨著時間常數 \(\tau = RC\text{ }\) 漸漸消失。
範例-5：汽車RC放電
|
當汽車在人行道上行駛時，電子首先從人行道移動到輪胎上，然後再到車身上。汽車存儲這種多餘的電荷和相關的電勢能，就好像車身是電容器的一個板，而路面是另一個板。當汽車停下來時，它會通過輪胎釋放多餘的電荷和能量，就像電容器可以通過電阻器放電一樣。如果一個導電物體在汽車放電前進入汽車幾厘米內，剩餘的能量會突然轉移到汽車和物體之間的火花上。假設導電物體是加油機。如果火花能量小於臨界值 \(U_{fire}=50\) mJ，火花將不會點燃燃料並引起火災。當圖中的汽車在時間 \(t = 0\) 停車時，汽車與地之間的電位差為 \(V_0 = 30\) kV。汽車對地電容為\(C= 500\) pF，每個輪胎的電阻為\(R_{tire}=100\) G\(\Omega\)。汽車需要多長時間才能通過輪胎排放到臨界值 \(U_{fire}\) 以下？ |
|
授課教師
陳永忠 ycchen@thu.edu.tw