當一個帶電粒子以垂直於磁場的方向上入射到磁場當中,帶電粒子將會受到的磁力作用,這個力量的方向垂直於磁場和粒子運動的速度方向。磁力與速度方向垂直,因此這個力量不會改變粒子運動的速度大小,只改變速度的方向。磁力對帶電粒子的作用方式,正好就是進行圓週運動物體所需要的向心力,因此帶電粒子在這樣的磁場中將會進行等速率圓週運動。利用磁力\(F_B\)就是向心力\(F_c\)的關係,我們可以推導出粒子進行圓週運動的半徑:
\[F_B=qvB; \quad F_c=\dfrac{m v^2}{r}\]
\[qvB=\dfrac{m v^2}{r}; \quad r=\dfrac{mv}{qB}\]
Part.1:磁場與磁力
正如我們所討論的,物理學的一個主要目標是研究電場如何在帶電物體上產生電力。一個密切相關的目標是研究磁場如何在(運動的)帶電粒子或磁性物體(如磁鐵)上產生磁力。如果您曾經了解過磁場,您可能已經對磁場有所了解用小磁鐵將便條貼在冰箱門上,或將信用卡靠近磁鐵時意外擦除信用卡。磁鐵通過其磁場作用於門或信用卡。磁場和磁力的應用數不勝數,每年都在迅速變化。這裡只是幾個例子。幾十年來,娛樂業依賴於錄音帶和錄像帶上音樂和圖像的磁性記錄。儘管數字技術已在很大程度上取代了磁記錄,但該行業仍然依賴於控制 CD 和 DVD 播放器以及計算機硬盤驅動器的磁鐵;磁鐵還驅動耳機、電視、計算機和電話中的揚聲器錐體。現代汽車配備了數十個磁鐵,因為它們用於發動機點火、自動車窗控制、天窗控制和擋風玻璃雨刷控制的電機中。大多數安全警報系統、門鈴和自動門鎖都使用磁鐵。簡而言之,你被磁鐵包圍著。磁場科學是物理學;磁場的應用是工程。科學和應用都始於“什麼產生磁場?”這個問題。因為電場是由電荷產生的,我們可以合理地認為磁場是由磁荷產生的。儘管某些理論預測存在單個磁荷(稱為磁單極子),但它們的存在尚未得到證實。那麼磁場是如何產生的呢?有兩種方法。一種方法是使用移動的帶電粒子(例如電線中的電流)來製造電磁體。電流產生的磁場可用於控制計算機硬盤驅動器或分揀廢金屬。在下一個單元中,我們將討論電流產生的磁場。
產生磁場的另一種方法是通過電子等基本粒子,因為這些粒子周圍有一個內在的磁場。也就是說,磁場是每個粒子的基本特徵,正如質量和電荷(或不帶電荷)是基本特徵一樣。某些材料中電子的磁場相加得到材料周圍的淨磁場。這種添加是用於懸掛冰箱紙幣的永磁體具有永磁場的原因。在其他材料中,電子的磁場相互抵消,在材料周圍沒有產生淨磁場。這種取消是您的身體周圍沒有永久磁場的原因,這很好,否則您可能會在每次經過冰箱門時被猛烈撞擊。本章的第一項工作是定義磁場。我們利用實驗事實來定義磁場,即當帶電粒子在磁場中移動時,磁力會作用在粒子上。
磁場與磁力
由於粒子的加速度是可測量的,我們可以通過將測量的加速度(a)乘以粒子的質量(m)來獲得力(F)的定量值,\(F=ma\)。 因此,我們可以使用磁力定律,方程: \[\vec{F}=q \vec{v} \times \vec{B}\] 通過測量 \(Q,\, v\)和 \(F\)來量化磁場\(B\)。這為我們提供了以下磁場的操作定義:如果以 1 m/s 的速度垂直於磁場運動的帶電粒子 1 C 上的力受到大小為 1 N 的力,則磁場 B 等於一個單位的磁場。
磁場的單位稱為特斯拉(Tesla),用字母 T 表示。 我們可以用 kg/A.s2=T 的基本單位來寫特斯拉。可以用各種其他方式表達特斯拉,例如 V.s/m2。對於地球物理測量來說,1特斯拉是一個太大的單位,而另外一個經常被使用的磁場單位是高斯(G, Gauss)。
高斯與特斯拉的換算關係如下:
1 G=10-4 T; 1 T = 104 G。
地球磁場約為 0.5 高斯,而冰箱磁鐵的磁場約為0.1特斯拉,磁共振成像 (MRI, magnetic resonace image)機器中使用的磁場約為 2 特斯拉。給出了自然界和實驗室中磁場的一些典型值,以便您了解各種情況下的數量級。 如您所見,自然界中的磁場變化超過 18 個數量級,從最小於星際空間中的10-10T到中子星中的 108 T。
Typical Magnetic Fields (from various sources) -------------------------------------------------- Location Magnetic Field (T) Neutron star surface 108 Superconducting magnet 5 Small bar magnet 1 Earth's Surface 0.5x10-4 Interstellar space 10-10 --------------------------------------------------
洛倫茲力
帶電粒子可以承受與電荷量成正比的兩種力,即電力和磁力。電荷上的淨力稱為洛倫茲力或電磁力,它是電荷上的電力和磁力的向量和。 \begin{equation} \vec F_{\text{em}} = q\left(\vec E + \vec v\times \vec B \right) \end{equation} 注意電荷 \(q\) 的符號在這裡對於確定力的方向很重要。帶電粒子在同時存在電場和磁場的環境中的運動,粒子運動的軌跡是由牛頓第二運動來決定。磁偶極矩
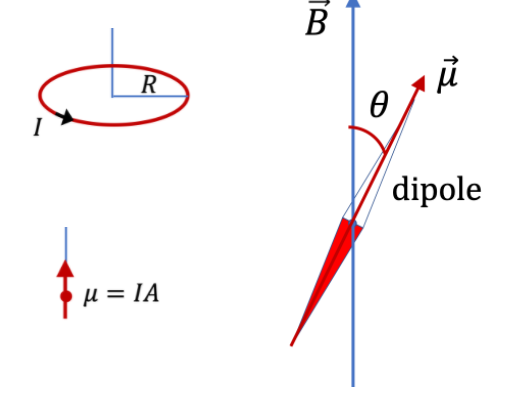 從根本上說,磁鐵由微觀磁鐵組成。例如,電子本身就是一個微小的磁鐵。每個微觀磁體,即使是單個電子作為磁體,總是由北極和南極組成。也就是說,每個磁鐵都由磁偶極子組成。在電偶極子的情況下,我們定義了一個稱為偶極矩的量,它等於電荷與兩個電荷之間的距離的乘積(\(\vec{p}=q\vec{d}\))。儘管我們沒有單獨的正負磁荷,但我們仍然可以通過將微小磁鐵置於外部磁場中時的行為方式來定義磁偶極矩。我們用向量\(\vec{\mu}\)來表示磁偶極矩。構成磁偶極的實際組成可能小至基本粒子例如電子、質子(這種基本粒子除了帶有電荷,還帶了磁場就是磁矩),也可能是一個電流環,在下一個單元中我們會介紹電流的磁效應,圓環電流能夠產生磁場。
從根本上說,磁鐵由微觀磁鐵組成。例如,電子本身就是一個微小的磁鐵。每個微觀磁體,即使是單個電子作為磁體,總是由北極和南極組成。也就是說,每個磁鐵都由磁偶極子組成。在電偶極子的情況下,我們定義了一個稱為偶極矩的量,它等於電荷與兩個電荷之間的距離的乘積(\(\vec{p}=q\vec{d}\))。儘管我們沒有單獨的正負磁荷,但我們仍然可以通過將微小磁鐵置於外部磁場中時的行為方式來定義磁偶極矩。我們用向量\(\vec{\mu}\)來表示磁偶極矩。構成磁偶極的實際組成可能小至基本粒子例如電子、質子(這種基本粒子除了帶有電荷,還帶了磁場就是磁矩),也可能是一個電流環,在下一個單元中我們會介紹電流的磁效應,圓環電流能夠產生磁場。磁偶極矩放置在外部磁場\(\vec{B}\)中,我們發現微小的磁鐵傾向於與外部磁場同向對齊。如果外部磁場是均勻的,偶極子上就沒有淨力。但是,如果偶極子未與磁場對齊,則偶極子上會產生力矩。力矩向量\(\vec{\tau}\)如下: \[\vec{\tau}=\vec{\mu} \times \vec{B}\] 力矩的大小: \[|\vec{\tau}|=\mu B \sin \theta \] 其中\(\theta\)是偶極子和場之間的角度。
磁偶極矩的單位:\(\mu\)的單位 = \(\tau\)的單位/ \(B\) 的單位 = N.m/T = J/T。我們會發現這個單位也可以表示為Am2。在這些單位中,電子的固有磁偶極矩約為 \(9.28 \times 10^{-24}\) J/T。
由於力矩,在外部磁場中改變磁偶極矩的方向需要消耗能量。類似於電偶極子在電場中的轉動一樣的方式,假設磁偶極子相對於外部磁場初始定向於角度\(\theta_i\),若外界做功將其方向更改為角度\(\theta_f\),則做功如下: \[W=-\mu B \cos \theta_f + \mu B \cos \theta_i \] 這將等於兩個方向之間偶極子的磁位能變化\(\Delta U\)。假設磁偶極矩的方向相對於磁場方向為 90° 時取磁位能為零,則得到角度為 θ 時的磁位能公式如下。 \[ U(\theta)=-\mu B \cos \theta = -\vec{\mu} \cdot \vec{B}\] 這個公式表示磁偶極子與磁場同方向時磁位能最低,反方向時磁位能最高。
磁場中的運動
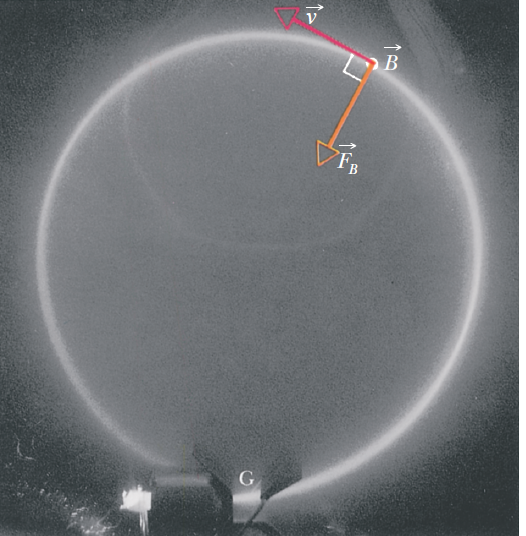 在右圖當中我們可以看見,把帶負電的電子射進一個均勻的磁場當中,磁場的方向是從紙張背面指向外面的方向,根據向量的外積運算,速度向量\(\vec{v}\),與磁場向量\(\vec{B}\)的外積產生一個半徑朝外的向量\(\vec{v} \times \vec{B}\)。但是因為磁力還要包括電荷\(q\)的乘積,\(\vec{F}=q\vec{v} \times \vec{B}\),電子帶有負電,因此磁力倒過來指向圓心。這個力量不能改變電子的速度大小,但是可以改變電子的速度方向,因為一直指向圓心,因此形成了一個圓週運動所需要的向心力,電子就會在磁場中進行圓週運動。我們在這一個小節就要探討帶電粒子在磁場中所進行的圓週運動。
在右圖當中我們可以看見,把帶負電的電子射進一個均勻的磁場當中,磁場的方向是從紙張背面指向外面的方向,根據向量的外積運算,速度向量\(\vec{v}\),與磁場向量\(\vec{B}\)的外積產生一個半徑朝外的向量\(\vec{v} \times \vec{B}\)。但是因為磁力還要包括電荷\(q\)的乘積,\(\vec{F}=q\vec{v} \times \vec{B}\),電子帶有負電,因此磁力倒過來指向圓心。這個力量不能改變電子的速度大小,但是可以改變電子的速度方向,因為一直指向圓心,因此形成了一個圓週運動所需要的向心力,電子就會在磁場中進行圓週運動。我們在這一個小節就要探討帶電粒子在磁場中所進行的圓週運動。
為了進一步簡化情況,只考慮帶電粒子在均勻磁場中進行的運動。一個帶電荷\(q\)的粒子以垂直於磁場的速度\(v\)進入恆定均勻磁場\(B\)的區域,則它的運動是圓周運動,圓的半徑是\(r\),牛頓定律採用以下形式: \[qvB=\dfrac{m v^2}{r}; \quad r=\dfrac{m v}{q B}\] 圓週運動的速度和週期有關:\(v=\dfrac{2 \pi r}{T}; \quad v=r \omega\)把這個關係式代入上式我們可以得到帶電粒子在磁場中進行圓週運動的週期(\(T\))、頻率(\(f\))和角頻率(\(\omega\)): \[ \omega =\dfrac{q B}{m}, \quad f =2 \pi \omega=\dfrac{2 \pi q B}{m}, \quad T =\dfrac{m}{2 \pi q B} \] \(T、f 和\omega\)不取決於粒子的速度(假設速度遠小於光速)。快粒子在大圓中運動,慢粒子在小圓圈中運動,但所有具有相同荷質比 |q|/m 的粒子都在相同的時間\(T\)(週期)來完成一周的運動。
螺旋路徑(helical path)
如果帶電粒子的速度具有平行於(均勻)磁場的分量,則粒子將圍繞場矢量的方向沿螺旋路徑移動。這種粒子的速度矢量分解為兩個分量,一個平行於磁場,一個垂直於它:平行分量\(v_{\parallel}\)決定了螺旋的螺距\(p\),即相鄰匝之間的距離。垂直分量\(v_{\perp}\)決定了螺旋的半徑,是上列方程式中要替代 \(v\) 的量。
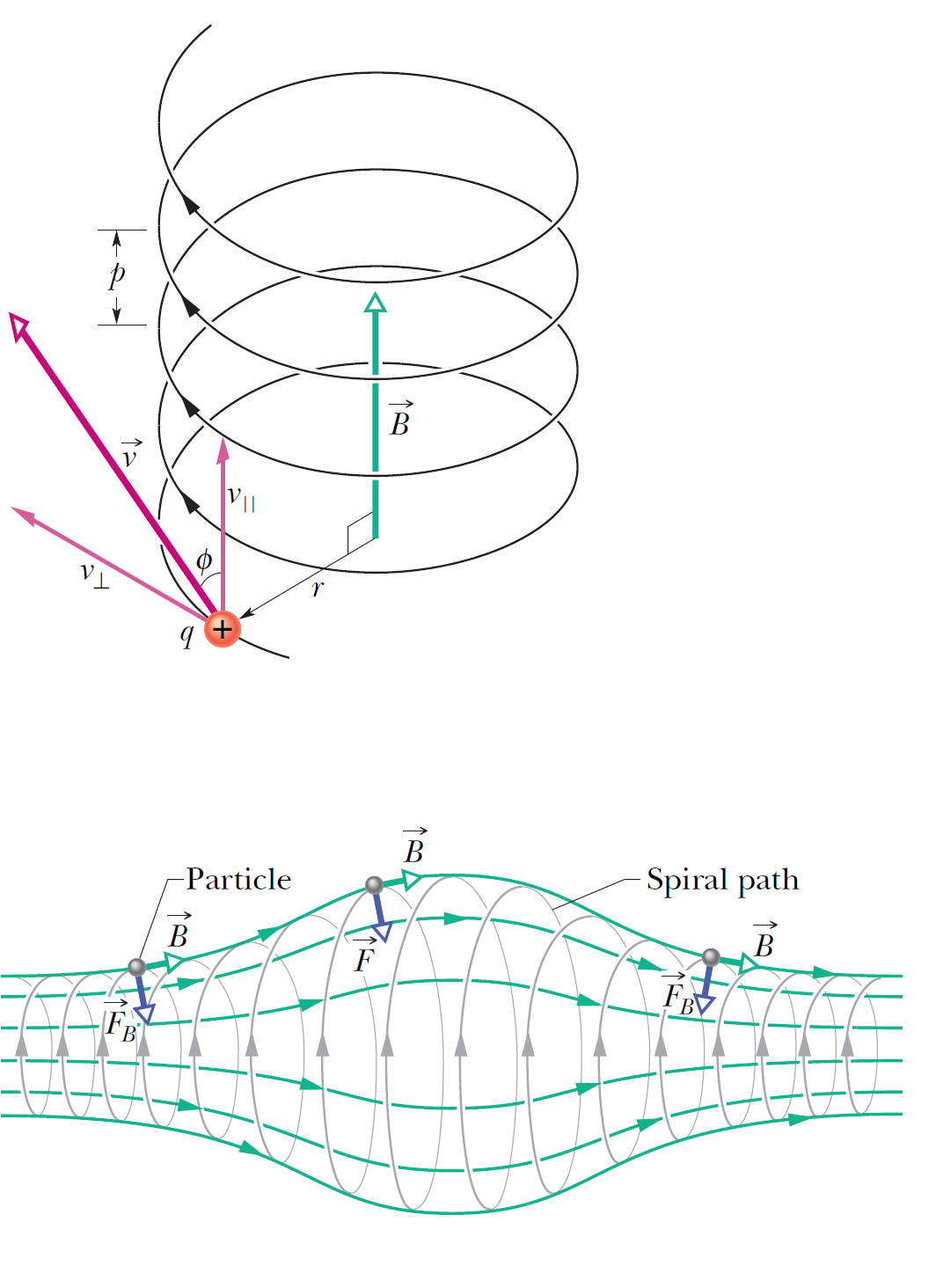 假設磁場沿z軸,粒子的速度與z軸成θ角。粒子繞z軸沿螺旋路徑運動,在圓周運動中的角速度\(\omega=\dfrac{qB}{m}\),螺旋路徑的螺距\(p\)
\[p=v_{\parallel} T=\dfrac{v \cos \theta (2 \pi)}{\omega}=\dfrac{v \cos \theta (2 \pi)m}{q B}\]
,螺旋中環的半徑\(r\)
\[r = \dfrac{m v_{\perp}}{qB}=\dfrac{m v \sin \theta}{qB} .\]
我們來考慮一個非均勻的磁場,這樣的磁場可以想像是由兩個電流環,相隔一個距離平行放置,所產生的磁場結構,如右圖所示。我們在下一個單元探討電流的磁效應的時候,會再詳細討論這個磁場的產生機制。從圖中我們可以看見,整體而言磁場的方向是從左邊指向右邊,幾乎是有一個固定的方向,但是又不全然如此。可以看見在中央地帶磁場的方向會向外擴張,造成磁力線的密度下降,代表在中央地帶的磁場大小較弱,兩端的磁場較強。一個帶電粒子如果在這樣的磁場當中運動的時候,會依循螺旋型的軌道運動,軌道的半徑與磁場成反比,因此在兩端的迴旋半徑較小,而在磁場中央地帶的迴旋半徑較大。圖中我們也可以看出帶電的粒子運動的時候不止是受到圓週運動的向心力,同時也有沿著磁場軸向的力分量,並且方向是指向中央的方向。因此在軸向上形成一個恢復力的作用,因此帶電粒子在軸向上的運動是一個簡諧運動。換句話說,帶電粒子除了在磁場中轉動之外,還會在磁場的軸向上來回振動,這是一個非常有趣的磁場結構,根據其幾何樣貌,我們把這樣的磁場稱為磁瓶子。
假設磁場沿z軸,粒子的速度與z軸成θ角。粒子繞z軸沿螺旋路徑運動,在圓周運動中的角速度\(\omega=\dfrac{qB}{m}\),螺旋路徑的螺距\(p\)
\[p=v_{\parallel} T=\dfrac{v \cos \theta (2 \pi)}{\omega}=\dfrac{v \cos \theta (2 \pi)m}{q B}\]
,螺旋中環的半徑\(r\)
\[r = \dfrac{m v_{\perp}}{qB}=\dfrac{m v \sin \theta}{qB} .\]
我們來考慮一個非均勻的磁場,這樣的磁場可以想像是由兩個電流環,相隔一個距離平行放置,所產生的磁場結構,如右圖所示。我們在下一個單元探討電流的磁效應的時候,會再詳細討論這個磁場的產生機制。從圖中我們可以看見,整體而言磁場的方向是從左邊指向右邊,幾乎是有一個固定的方向,但是又不全然如此。可以看見在中央地帶磁場的方向會向外擴張,造成磁力線的密度下降,代表在中央地帶的磁場大小較弱,兩端的磁場較強。一個帶電粒子如果在這樣的磁場當中運動的時候,會依循螺旋型的軌道運動,軌道的半徑與磁場成反比,因此在兩端的迴旋半徑較小,而在磁場中央地帶的迴旋半徑較大。圖中我們也可以看出帶電的粒子運動的時候不止是受到圓週運動的向心力,同時也有沿著磁場軸向的力分量,並且方向是指向中央的方向。因此在軸向上形成一個恢復力的作用,因此帶電粒子在軸向上的運動是一個簡諧運動。換句話說,帶電粒子除了在磁場中轉動之外,還會在磁場的軸向上來回振動,這是一個非常有趣的磁場結構,根據其幾何樣貌,我們把這樣的磁場稱為磁瓶子。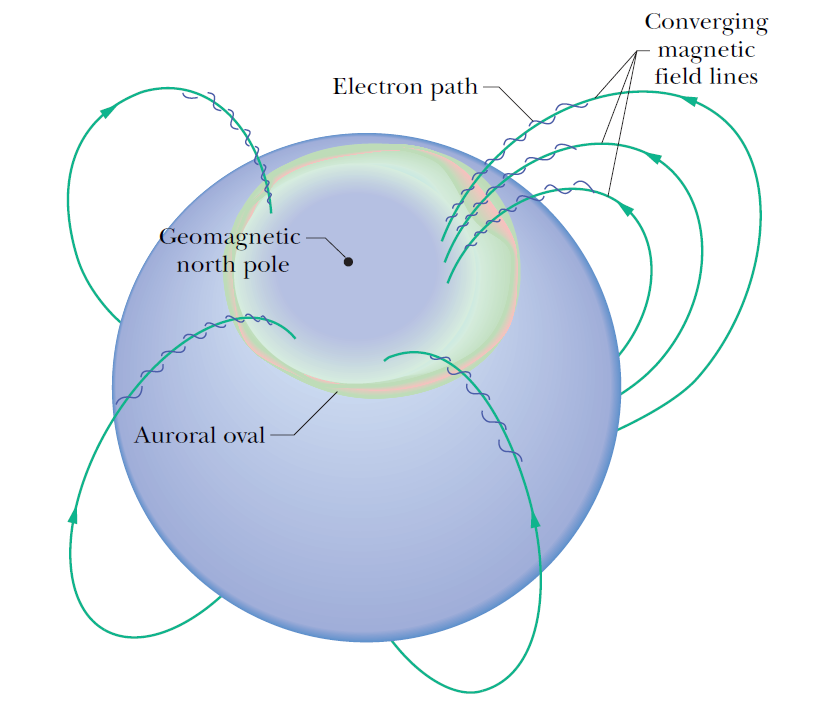 極光是地球天空中的自然光顯示,主要出現在高緯度地區(北極和南極周圍)。極光顯示出絢麗光的動態圖案,展現像是覆蓋整個天空的窗簾、光線、螺旋或動態閃爍。極光是太陽風引起的磁層擾動的結果。這些擾動改變了磁層等離子體中帶電粒子的軌跡。這些粒子,主要是電子和質子,沉澱到高層大氣中。高速運動的電子和質子撞擊大氣成分,造成氣體分子的電離和激發,因而發出不同顏色和多彩的光。在兩個極區內出現的極光的形式也取決於施加給帶電粒子的加速度的力。太陽系中的大多數行星、天然衛星、矮行星,甚至彗星也有極光。
極光是地球天空中的自然光顯示,主要出現在高緯度地區(北極和南極周圍)。極光顯示出絢麗光的動態圖案,展現像是覆蓋整個天空的窗簾、光線、螺旋或動態閃爍。極光是太陽風引起的磁層擾動的結果。這些擾動改變了磁層等離子體中帶電粒子的軌跡。這些粒子,主要是電子和質子,沉澱到高層大氣中。高速運動的電子和質子撞擊大氣成分,造成氣體分子的電離和激發,因而發出不同顏色和多彩的光。在兩個極區內出現的極光的形式也取決於施加給帶電粒子的加速度的力。太陽系中的大多數行星、天然衛星、矮行星,甚至彗星也有極光。我們地球的磁場從南極發出深入地表上空的太空當中,再由地球的北極回到地球表面。地球的磁場不是均勻的,因此會展現出磁瓶子的特性,在地球外圍的太空中高速運動的帶電粒子,在非常接近地球的時候會被地球磁瓶子捕獲而進入磁瓶子中運動。被捕獲的粒子形成範艾倫輻射帶,它在地球南北磁極之間的地球大氣層上方環繞。這些粒子在幾秒鐘內從磁性瓶的一端到另一端來回反彈。當一個巨大的太陽耀斑將高能的電子和質子射入輻射帶時,電子通常在反射的區域會產生電場。這個場消除了磁場反射,於是該電場將電子驅動到非常接近地表的大氣中,在那裡它們與空氣中的原子和分子碰撞,使空氣發光。這種光形成了極光。這是一種懸掛在大約海拔100公里高度的光幕。綠光是由氧原子發出的,粉紅光是由氮分子發出的,但通常光線太暗,我們只能感受到白光。雖然極光很長,但它只有大約 100 m 厚(從北到南),因為產生它的電子的路徑會隨著電子沿著會聚的磁場線螺旋下降而會聚。
例題-1
A magnet brought near an old-fashioned TV screen severely distorts its picture by altering the path of the electrons that make its phosphors glow. To illustrate this, calculate the radius of curvature of the path of an electron having a velocity of \(6.0 \times 10^7\) m/s (corresponding to the accelerating voltage of about 10.0 kV used in some TVs) perpendicular to a magnetic field of strength \(B=0.50\) T (obtainable with permanent magnets).
一塊磁鐵靠近老式電視屏幕,通過改變使熒光粉發光的電子路徑,嚴重扭曲了它的畫面。 為了說明這一點,計算速度為 \(6.0 \times 10^7\) m/s 的電子路徑的曲率半徑(對應於某些電視中使用的約 10.0 kV 的加速電壓),垂直於 磁場強度 \(B=0.50\) T(可通過永磁體獲得)。
\[r=\dfrac{mv}{qB}=\dfrac{9.11 \times 10^{-31}}{6.0 \times 10^7}=6.83 \times 10^{-4} \, \text{m}\]
一塊磁鐵靠近老式電視屏幕,通過改變使熒光粉發光的電子路徑,嚴重扭曲了它的畫面。 為了說明這一點,計算速度為 \(6.0 \times 10^7\) m/s 的電子路徑的曲率半徑(對應於某些電視中使用的約 10.0 kV 的加速電壓),垂直於 磁場強度 \(B=0.50\) T(可通過永磁體獲得)。
\[r=\dfrac{mv}{qB}=\dfrac{9.11 \times 10^{-31}}{6.0 \times 10^7}=6.83 \times 10^{-4} \, \text{m}\]
例題-2
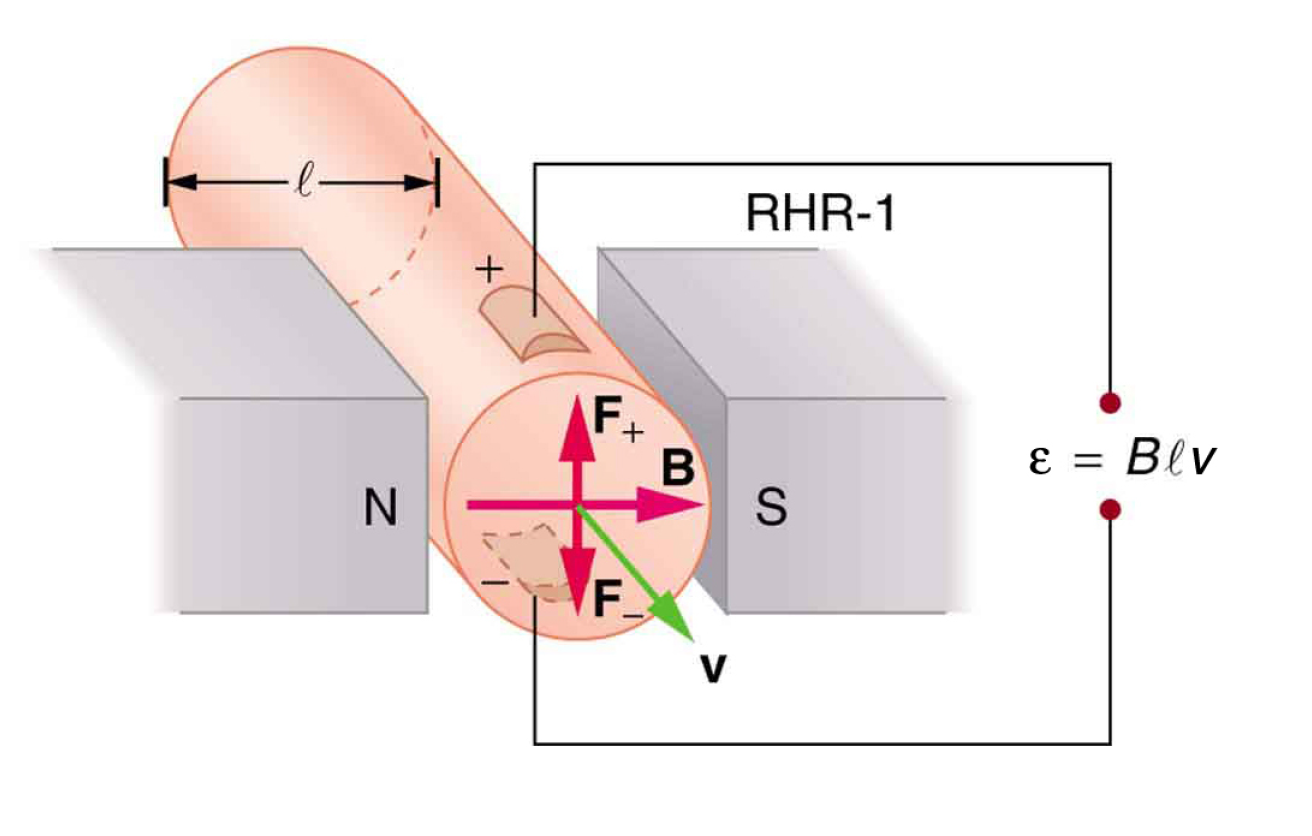 A Hall effect flow probe is placed on an artery, applying a 0.100-T magnetic field across it, in a setup similar to that in figure. What is the Hall emf, given the vessel’s inside diameter is 4.00 mm and the average blood velocity is 20.0 cm/s?
A Hall effect flow probe is placed on an artery, applying a 0.100-T magnetic field across it, in a setup similar to that in figure. What is the Hall emf, given the vessel’s inside diameter is 4.00 mm and the average blood velocity is 20.0 cm/s? 霍爾效應流量探頭放置在動脈上,在其上施加 0.100-T 的磁場,設置類似於圖中的設置。 假設血管內徑為 4.00 mm,平均血流速度為 20.0 cm/s,霍爾電動勢是多少?
\[\mathscr{E}=Blv=(0.1)(4 \times 10^{-3})(0.2)=80.0 \,\mu\text{V}\]
例題-3
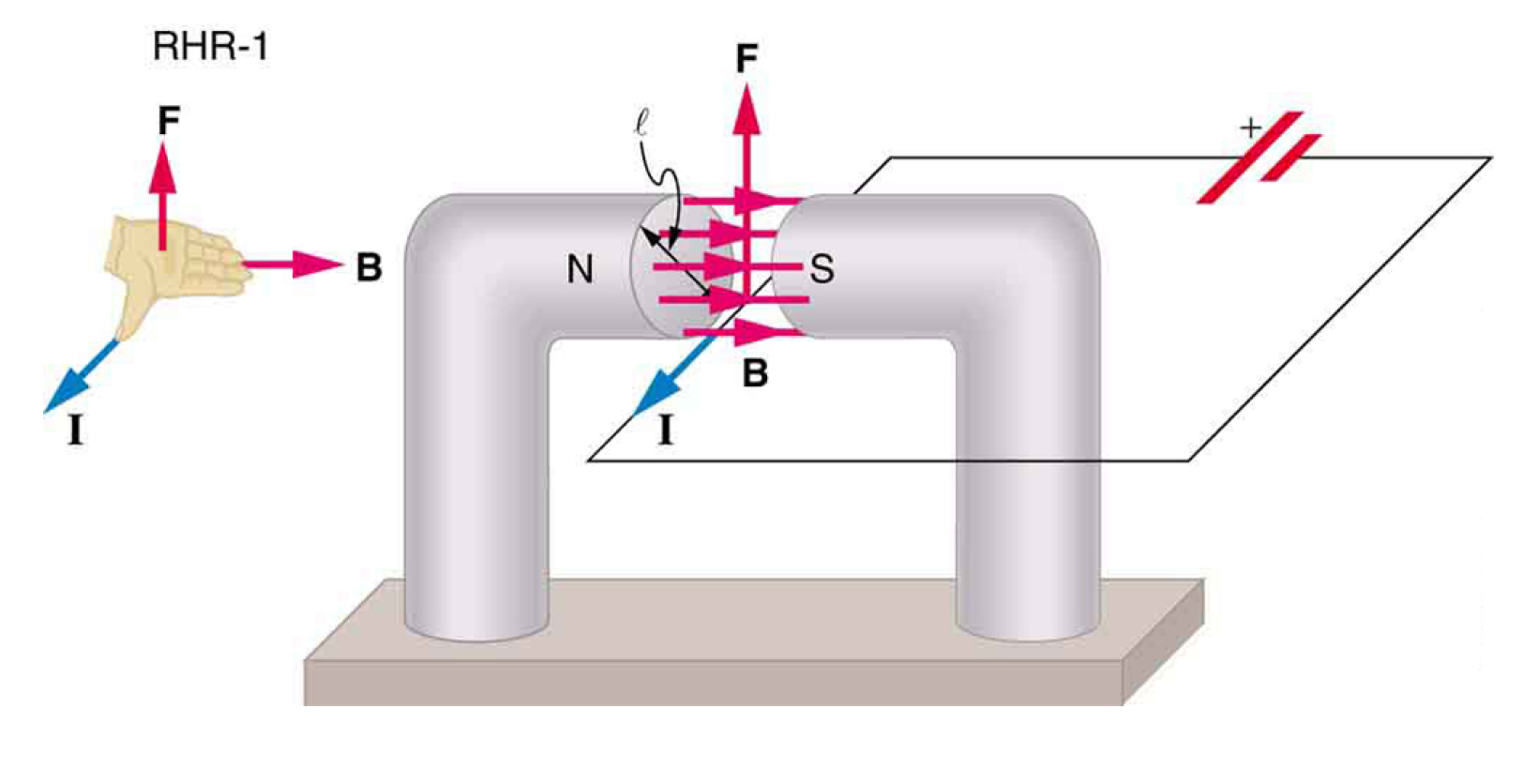 Calculate the force on the wire shown in the figure, given \(B=1.50 \, \text{T}, \, l=5.0 \, \text{cm}, \,I=20.0 \, \text{A}\).
Calculate the force on the wire shown in the figure, given \(B=1.50 \, \text{T}, \, l=5.0 \, \text{cm}, \,I=20.0 \, \text{A}\). 給定 \(B=1.50 \, \text{T}, \, l=5.0 \, \text{cm}, \,I=20.0 \, \text{A}\),計算圖中所示電線上的力。
\[F=I l B \sin \theta=(20)(0.05)(1.5) \sin 90^{\circ}=1.5 \, \text{N}.\]
PART.2:磁力的應用
在這個小節中我們要介紹如何應用磁場的磁力,控制帶電粒子的運動,因而產生一些科技上的應用,包括:質譜儀、迴旋加速器和同步加速器。質譜儀
 https://www.glowscript.org/#/user/ycchenofthu/folder/0GPN/program/GPN2-mass-spectrum.py
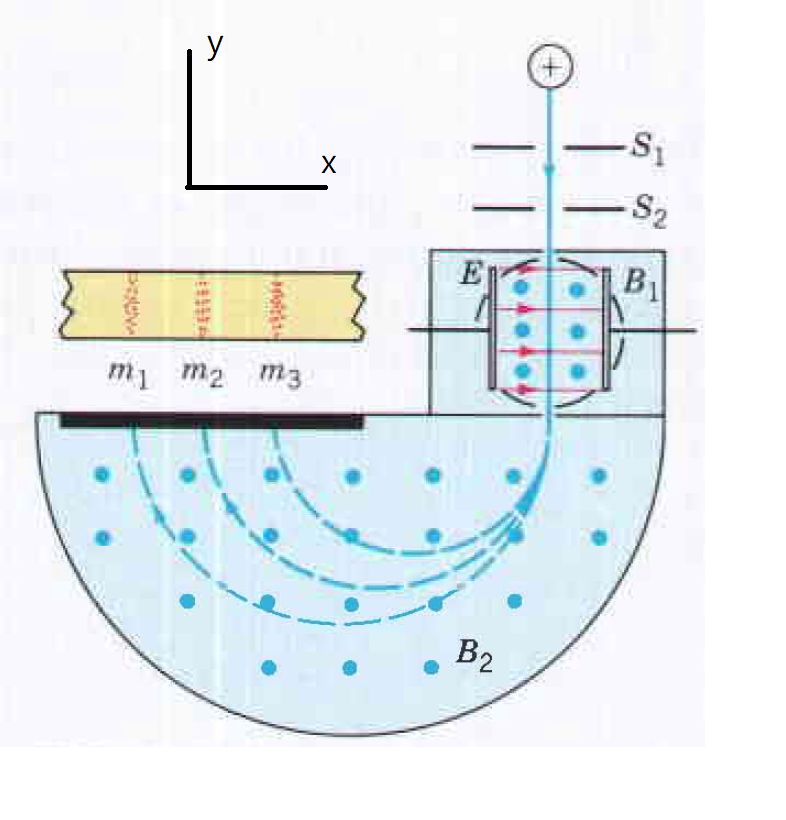
質譜(mass spectrometry)是一種電離化學物質並根據其質荷比(質量-電荷比,m/q)對其進行排序的分析技術。簡單來說,質譜儀測量樣品組成分子的質量。質譜法被用於許多不同領域,並被用於純樣品和複雜混合物。質譜是離子訊號作為質荷比的函數的曲線圖。這些頻譜被用於確定樣品的元素或同位素,顆粒和分子的質量,並闡明分子的化學結構。在典型的質譜法中,可以是固體,液體或氣體的樣品被電離,例如用電子轟擊它。這可能導致一些樣品的分子破碎成帶電的碎片。然後,這些離子根據其質荷比被分離,通常通過加速它們並使其經受電場或磁場:相同質荷比的離子將經歷相同數量的偏轉,具有相同帶電量的粒子,質量較小的會落差較大的半徑上,質量較大的會落在較小的半徑上,因此不同質量的粒子會依循不同的軌道半徑,落在接收器不同的位置,因此可以鑑別不同的組成份子。
https://www.glowscript.org/#/user/ycchenofthu/folder/0GPN/program/GPN2-mass-spectrum.py
質譜(mass spectrometry)是一種電離化學物質並根據其質荷比(質量-電荷比,m/q)對其進行排序的分析技術。簡單來說,質譜儀測量樣品組成分子的質量。質譜法被用於許多不同領域,並被用於純樣品和複雜混合物。質譜是離子訊號作為質荷比的函數的曲線圖。這些頻譜被用於確定樣品的元素或同位素,顆粒和分子的質量,並闡明分子的化學結構。在典型的質譜法中,可以是固體,液體或氣體的樣品被電離,例如用電子轟擊它。這可能導致一些樣品的分子破碎成帶電的碎片。然後,這些離子根據其質荷比被分離,通常通過加速它們並使其經受電場或磁場:相同質荷比的離子將經歷相同數量的偏轉,具有相同帶電量的粒子,質量較小的會落差較大的半徑上,質量較大的會落在較小的半徑上,因此不同質量的粒子會依循不同的軌道半徑,落在接收器不同的位置,因此可以鑑別不同的組成份子。根據右圖的質譜儀結構我們來述說其工作原理。首先由帶電的粒子源射出帶電的粒子,帶電的粒子經過平行板\(S_1 \, S_2\),\(S_1,\, S_2\)的兩個開口具有定向的作用,也就是穿過平行板的粒子,飛行的方向必然在中心線上,朝著\(-\hat{j}\)的方向飛行。經過平行板\(S_1 \, S_2\)的加速之後,帶電粒子進入一個所謂速度選擇器的空間當中。在速度選擇器中架設了互相垂直的電場和磁場,電場的方向向右\(\hat{i}\),磁場的方向指向紙張的外部\(\hat{k}\)。假設帶電粒子帶正電,因此帶電粒子在穿越平行板的區域時,會遭受到向右的電力\(\hat{F_e}=\hat{i}\)。根據磁力的作用 \[\vec{F}_m=q \vec{v} \times \vec{B}, \quad \hat{v}=-\hat{j};\, \hat{B}=\hat{k}, \quad \vec{v} \times \vec{B} \text{指向} \hat{i}, \quad \hat{F}_m=-\hat{i},\] 磁力的方向相左\(\hat{F}_m=-\hat{i}\)。 因此這兩個力量會互相抵銷,如果兩個力量的大小相同合力為零,帶電粒子將不會偏移中心飛行的路線,而能夠穿越速度選擇器正下方的出口,進入下方的磁場\(B_2\)區域。根據電力與磁力相等這個條件我們會發現只有速度滿足下面關係的粒子才能夠順利的穿過速度選擇器: \[F_e=F_m; \quad qE=qvB_1; \quad v=\dfrac{E}{B_1}\] 不滿足這個條件的速度不滿足\(v=\dfrac{E}{B_1}\)的粒子都會被擋在速度選擇器的內部,因此只要能夠進入下方\(B_2\)磁場區域的帶電粒子,其速度都確定了。雖然我們並不知道這些粒子的帶電量(q)和質量(m),但是他們的速度已經被確定了。
 進入下方磁場的粒子會在該區域中磁場的作用下進行圓週運動,最後會落在粒子收集器不同的位置。如果粒子的帶電量相同,那麼不同的位置就代表不同質量的粒子,因此就達到質譜儀分離不同質量粒子的目的:
\begin{align}
r \amp =\dfrac{m v}{q B_2} =\dfrac{mE}{q B_1 B_2} \\ \\
\dfrac{m}{q} \amp =\dfrac{B_1 B_2 r}{m E}
\end{align}
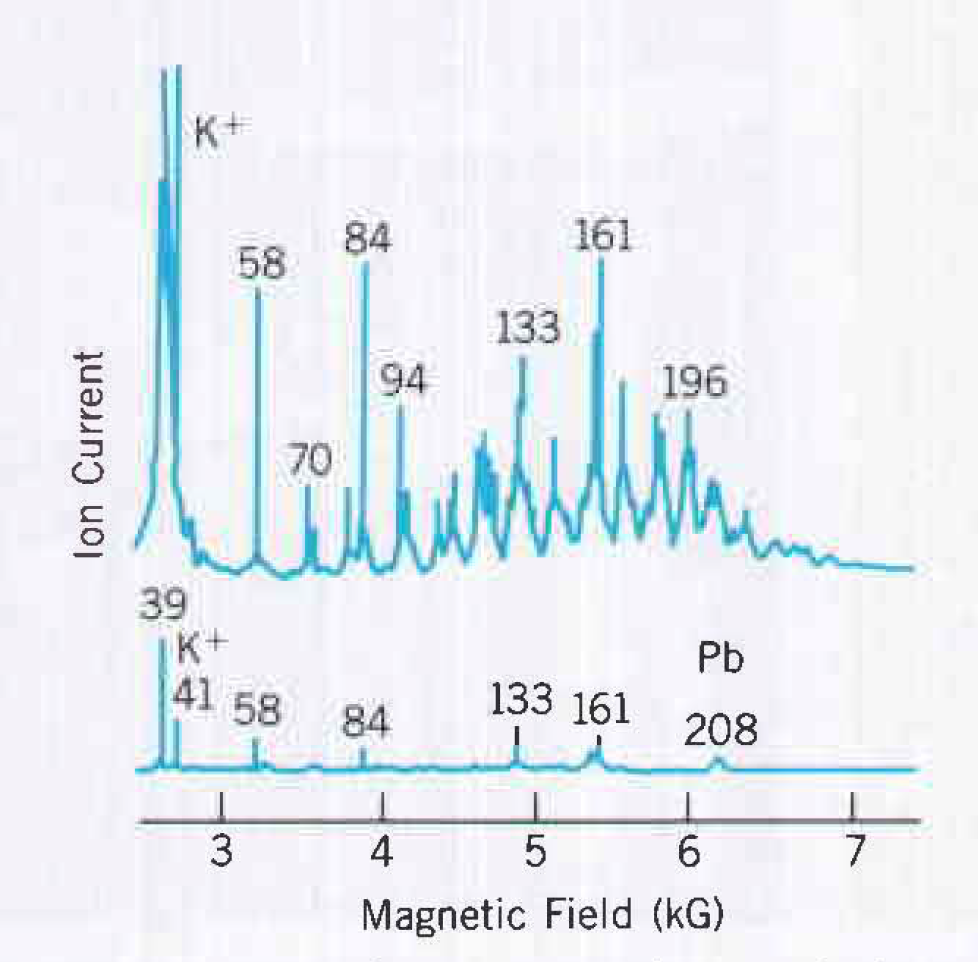
MS技術用於分離具有相同化學性質,但質量略有不同的同位素原子(兩個原子具有相同的質子數量但是有不同的中子數量)。 使用MS儀器可以檢測到約 0.01% 的質量差異。照片上痕蹟的密度也產生了粒子的相對豐度。質譜法通常用於化學分析,例如檢測污染物或雜質。右圖所呈現的是抽一根煙前後,房間內空氣的質譜圖。 84 和 161 處的峰值是由尼古丁引起的。
進入下方磁場的粒子會在該區域中磁場的作用下進行圓週運動,最後會落在粒子收集器不同的位置。如果粒子的帶電量相同,那麼不同的位置就代表不同質量的粒子,因此就達到質譜儀分離不同質量粒子的目的:
\begin{align}
r \amp =\dfrac{m v}{q B_2} =\dfrac{mE}{q B_1 B_2} \\ \\
\dfrac{m}{q} \amp =\dfrac{B_1 B_2 r}{m E}
\end{align}
MS技術用於分離具有相同化學性質,但質量略有不同的同位素原子(兩個原子具有相同的質子數量但是有不同的中子數量)。 使用MS儀器可以檢測到約 0.01% 的質量差異。照片上痕蹟的密度也產生了粒子的相對豐度。質譜法通常用於化學分析,例如檢測污染物或雜質。右圖所呈現的是抽一根煙前後,房間內空氣的質譜圖。 84 和 161 處的峰值是由尼古丁引起的。
迴旋加速器
通過用高能粒子轟擊原子靶可以獲得大量關於原子核和基本粒子性質的信息。 1932 年,英國的 J. Cockcroft 和 W. Walton 用加速了 700,000 V 的質子轟擊鋰靶,製造了第一台“原子粉碎機”。他們採用蠻力方法,直接建立了一個巨大的電位差。 1929 年,美國物理學家Ernest Lawrence想到了通過相對較小的電位差而不是邁出一大步來反復加速粒子的可能性。他與 M. S. Livingston 合作開發了稱為迴旋加速器的設備。第一個迴旋加速器建於 1930 年。迴旋加速器的運行是基於這樣一個事實: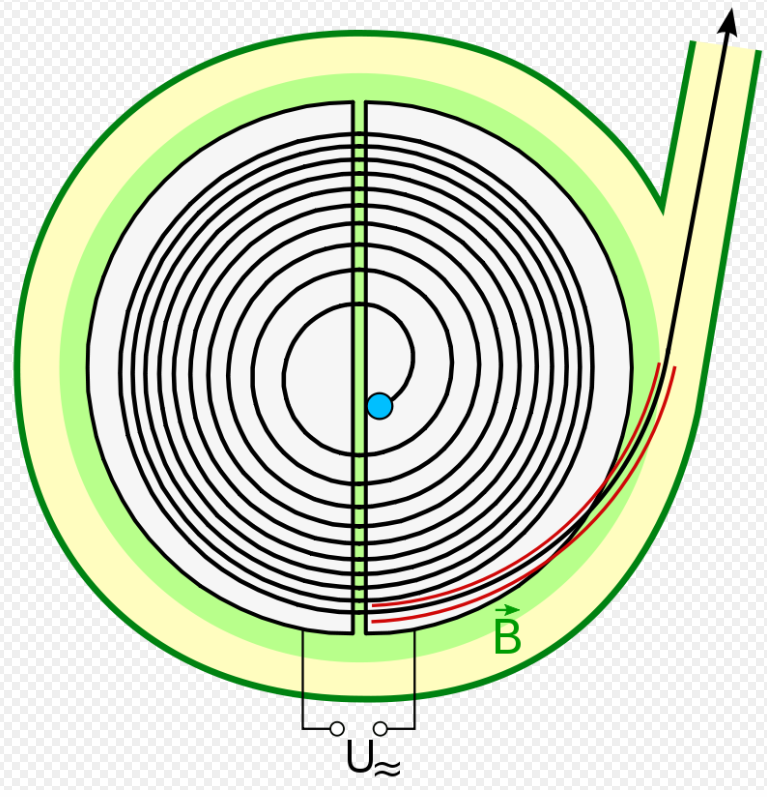
迴旋加速器,如圖所示,由兩個半圓柱體 \(D_1, \, D_2\)組成(以它們的形狀命名),它們由一個小間隙隔開並位於一個均勻的磁場中。帶電粒子,如質子或 α 粒子,由中心的離子源產生,並以一定的小速度注入其中一個\(D\)中。該裝置處於高真空中,盡可能地減少與空氣分子碰撞造成的損失。磁場穿透凹槽並導致粒子沿圓形路徑移動。\(D_1,\,D_2\)連接到一個高壓交流電源,該電源週期性的將其極性反轉,其周期選擇與粒子完成半圈所需的時間相匹配。與該電位差相關的電場主要局限於間隙。正如粒子完成第一個半圓一樣,\(D_1\)為正,\(D_2\)為負。由於這種極性加速了(正電)粒子穿過間隙,它們獲得動能: \[\Delta K=q V\] 並且因為速度增快,迴旋的半徑將會增加(\(r=\dfrac{mv}{qB}\)),因此會轉換到半徑更大的軌道上運動。在時間 \(T_{1/2}\)時,它們回到間隙處,但電位差已反轉其極性,因此它們再次加速穿過間隙。這個過程在間隙的許多次遍歷中重複:粒子總是加速穿過間隙並以越來越大的圓圈行進--但總是以相同的周期進行圓週運動。當粒子達到最大半徑時,偏轉板將它們引導到實驗區域。在實際應用中存在並發症。首先,很難在現代迴旋加速器的大面積(半徑約 2 m)上產生均勻的磁場。其次,隨著粒子加速,它的相對論質量變得明顯大於在低速下測量的通常質量。
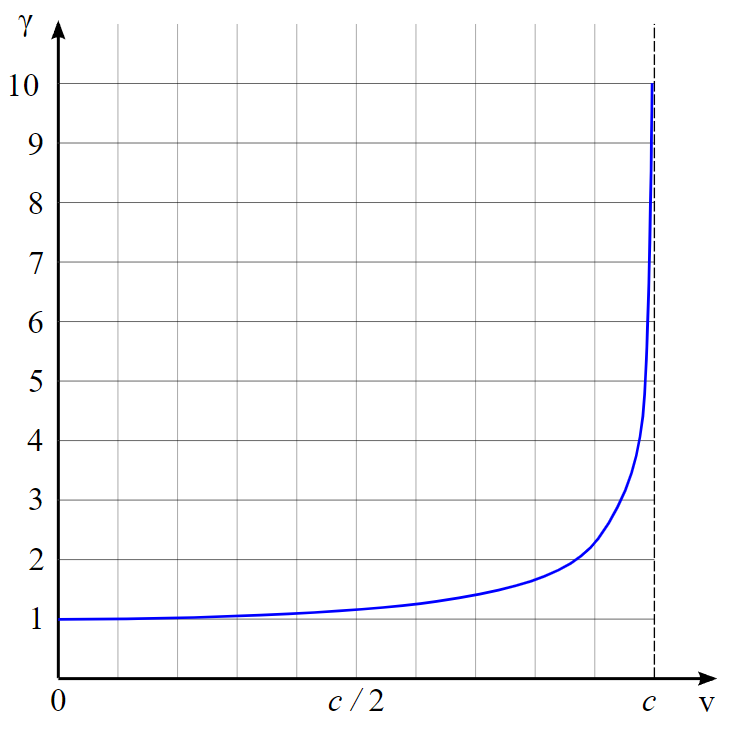 質量這一名詞在狹義相對論中通常是指物質在靜止時所測量的質量(靜質量)。這個意義的質量與牛頓力學的質量相同。不變質量是靜質量的另一名稱,但它通常是指由許多粒子構成的系統。相對論性質量這一名詞也被使用,而這是一個物體所具有的總能量。物體的相對論性質量包括了它所具有的動能,因此取決於觀察者所處於的參考系。
\[m=\gamma m_0, \quad \gamma=\left( 1-\frac{v^2}{c^2} \right)^{-1/2}\]
質量這一名詞在狹義相對論中通常是指物質在靜止時所測量的質量(靜質量)。這個意義的質量與牛頓力學的質量相同。不變質量是靜質量的另一名稱,但它通常是指由許多粒子構成的系統。相對論性質量這一名詞也被使用,而這是一個物體所具有的總能量。物體的相對論性質量包括了它所具有的動能,因此取決於觀察者所處於的參考系。
\[m=\gamma m_0, \quad \gamma=\left( 1-\frac{v^2}{c^2} \right)^{-1/2}\]
同步加速器
 同步加速器(Synchrotron)是一種環形的粒子加速器,使用磁場(讓帶電粒子在運行中可以改變方向)及電場(加速帶電粒子)與運行中的帶電粒子束同步化操作。本是由阿爾瓦雷茨發展用以研究高能粒子之裝置。 粒子迴旋加速器使用均勻的磁場及固定頻率變化的電場加速帶電粒子,如果改變其中一項則為同步粒子迴旋加速器,兩者都改變則為同步加速器。粒子在粒子迴旋加速器中,從中心以螺旋軌道運行到腔壁時,粒子迴旋加速器的最大半徑限制了粒子最後所獲得的全部能量。另一方面若以增加磁場強度的方式來提高加速能量,也有其極限。所以有同步加速器的出現。同步加速器中的粒子束具有固定軌道,藉著改變參數使帶電粒子獲得能量,在真空的環境(儲存環)中不斷的運行。同步加速器中的儲存環包含了直線段與彎曲的部分,前後相連在一起。因此在結構上和粒子迴旋加速器有很大的不同。而儲存環中彎曲的部分會有許多磁鐵設施使粒子束改變運行方向;直線段的部分則設置高頻共振腔使用高能量的微波提供粒子加速所需的電場。最強大的現代化的粒子加速器使用的同步加速器設計版本。最大的同步型加速器大型強子對撞機(LHC)位於瑞士日內瓦附近,由歐洲核子研究組織(CERN)建造。 同步加速器可以克服粒子迴旋加速器所遇到的問題,可以使用一個較小的管子來傳送粒子束,管子旁可裝設許多聚焦用的磁鐵或其他設施。
同步加速器(Synchrotron)是一種環形的粒子加速器,使用磁場(讓帶電粒子在運行中可以改變方向)及電場(加速帶電粒子)與運行中的帶電粒子束同步化操作。本是由阿爾瓦雷茨發展用以研究高能粒子之裝置。 粒子迴旋加速器使用均勻的磁場及固定頻率變化的電場加速帶電粒子,如果改變其中一項則為同步粒子迴旋加速器,兩者都改變則為同步加速器。粒子在粒子迴旋加速器中,從中心以螺旋軌道運行到腔壁時,粒子迴旋加速器的最大半徑限制了粒子最後所獲得的全部能量。另一方面若以增加磁場強度的方式來提高加速能量,也有其極限。所以有同步加速器的出現。同步加速器中的粒子束具有固定軌道,藉著改變參數使帶電粒子獲得能量,在真空的環境(儲存環)中不斷的運行。同步加速器中的儲存環包含了直線段與彎曲的部分,前後相連在一起。因此在結構上和粒子迴旋加速器有很大的不同。而儲存環中彎曲的部分會有許多磁鐵設施使粒子束改變運行方向;直線段的部分則設置高頻共振腔使用高能量的微波提供粒子加速所需的電場。最強大的現代化的粒子加速器使用的同步加速器設計版本。最大的同步型加速器大型強子對撞機(LHC)位於瑞士日內瓦附近,由歐洲核子研究組織(CERN)建造。 同步加速器可以克服粒子迴旋加速器所遇到的問題,可以使用一個較小的管子來傳送粒子束,管子旁可裝設許多聚焦用的磁鐵或其他設施。
授課教師
陳永忠 ycchen@thu.edu.tw