磁場
物理學的一個基本觀察是,運動的帶電粒子在其自身周圍產生磁場。因此,運動的帶電粒子的電流在電流周圍產生磁場。電磁學的這一特性是對電磁效應的綜合研究,讓發現它的人感到驚訝。不管你是否感到驚訝,這個功能在日常生活中變得非常重要,因為它是無數電磁設備的基礎。例如,電流產生的磁場可以在記錄或讀取磁性編碼磁帶和磁盤的機器中找到,例如老式計算機軟盤、盒式錄音帶和錄像帶。這種磁場也可以在磁力提升列車(磁懸浮列車)和其他用於提升重物的設備中找到。本章的第一步是確定一小段載流導線中的電流產生的磁場。然後我們將計算由於導線的幾種不同排列而產生的整個導線的磁場。Biot-Savart 定律
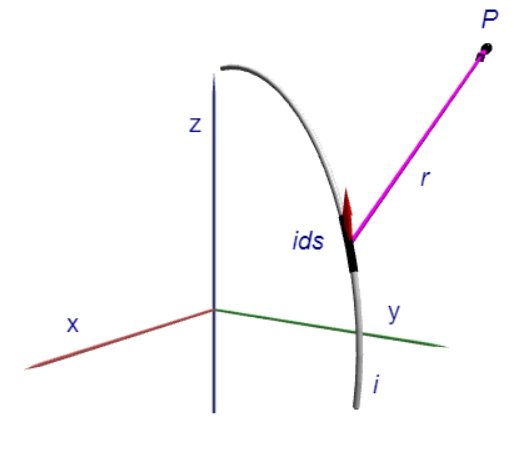 Biot-Savart定律為我們提供了獲取穩定電流產生磁場的計算法則。穩定電流是指電荷既不會在任何地方積累,也不會從電路中的任何地方耗盡。該定律使用電路中每個元素的貢獻疊加來獲得一個點的磁場。Biot-Savart定律具有復雜的數學形式,我們首先考慮一個無窮小的電流元素的Biot-Savart定律。在右圖中有一條電流線路,其中一小段微量電流\(id\vec{s}\)在\(P\)點所貢獻的磁場如下:
\[d\vec{B}_P = \dfrac{\mu_0 i}{4\pi} \, \dfrac{d\vec{s} \times \hat{r}}{r^2}\]
在比歐沙伐定律當中我們要強調兩個重點:1. 微量電流所產生的磁場與距離的平方成反比與電流的大小成正比,這個性質與電場類似。2.他們最大的不同在於兩種力量的方向,電力是一個向心力,電力的方向在電荷與場的連線上;但是磁場的方向並非如此,而且非常特別的,要使用一個向量外積的運算,來得到磁場的方向。
Biot-Savart定律為我們提供了獲取穩定電流產生磁場的計算法則。穩定電流是指電荷既不會在任何地方積累,也不會從電路中的任何地方耗盡。該定律使用電路中每個元素的貢獻疊加來獲得一個點的磁場。Biot-Savart定律具有復雜的數學形式,我們首先考慮一個無窮小的電流元素的Biot-Savart定律。在右圖中有一條電流線路,其中一小段微量電流\(id\vec{s}\)在\(P\)點所貢獻的磁場如下:
\[d\vec{B}_P = \dfrac{\mu_0 i}{4\pi} \, \dfrac{d\vec{s} \times \hat{r}}{r^2}\]
在比歐沙伐定律當中我們要強調兩個重點:1. 微量電流所產生的磁場與距離的平方成反比與電流的大小成正比,這個性質與電場類似。2.他們最大的不同在於兩種力量的方向,電力是一個向心力,電力的方向在電荷與場的連線上;但是磁場的方向並非如此,而且非常特別的,要使用一個向量外積的運算,來得到磁場的方向。為了計算整體導線電流所貢獻的磁場,我們可以透過對微量電流所產生的磁場進行積分就可以得到(這又是一次線性疊加原理的應用): \begin{equation} \vec B_P = \dfrac{\mu_0 i}{4\pi}\, \int_\text{circuit} \dfrac{d\vec s \times \hat r}{ r^2} \end{equation}
圓弧電流的磁場
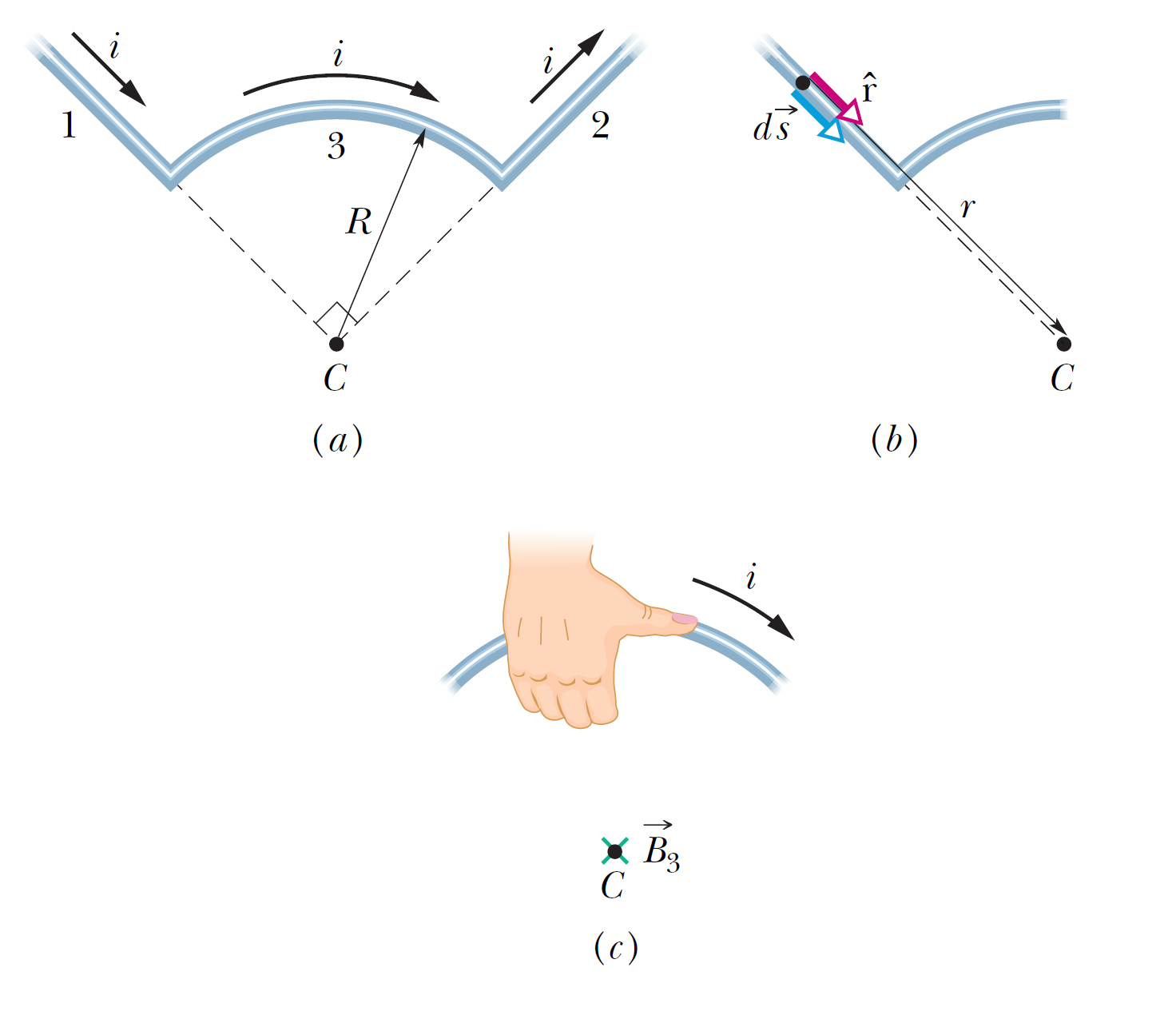 The wire in the figure carries a current i and consists of a circular arc of radius \(R\) and central angle \(\pi/2\) rad, and two straight sections whose extensions intersect the center \(C\) of the arc. What magnetic field \(B\) does the current produce at \(C\)?
The wire in the figure carries a current i and consists of a circular arc of radius \(R\) and central angle \(\pi/2\) rad, and two straight sections whose extensions intersect the center \(C\) of the arc. What magnetic field \(B\) does the current produce at \(C\)?圖中的導線載有電流 i,由半徑為 \(R\)、圓心角為 \(\pi/2\) rad 的圓弧以及延伸與中心 \(C\) 相交的兩條直線組成。計算電流在\(C\)處產生的磁場\(\{B}\)?
從圖形中我們可以看見電流直線1的電流微量元素\(d\vec{s}\)指向圓心的方向\(\hat{r}\)與微量元素的電流流向同方向,兩個向量的夾角為0度角,因此兩者的外積\(d\vec{s} \times \hat{r}=0\),也就是電流直線1沒有磁場的貢獻。同樣地,電流直線2的兩個向量夾角為180度,外積\(d\vec{s} \times \hat{r}=0\),也沒有磁場的貢獻。因此整個電流線路的磁場貢獻只需考慮圓弧3的部分。對於圓弧的電流流向\(id\vec{s}\)是在圓的切線方向,這個方向必然與圓心指向微量元素的徑向垂直\(d\vec{s} \perp \hat{r}=0\),因此我們可以很快地得到下面的結果: \begin{align*} \vec{B}_C =\vec{B}_3 &= \dfrac{\mu_0 i}{4\pi}\, \int_\text{3} \dfrac{d\vec{s} \times \hat{r}}{R^2} \\ &=\dfrac{\mu_0 i}{4\pi}\, \dfrac{R \pi/2}{R^2} (-\hat{k}) \\ &=\dfrac{\mu_0 i}{8R} (-\hat{k}) \end{align*} \((-\hat{k})\)指向紙張的內部。
長直導線電流的磁場
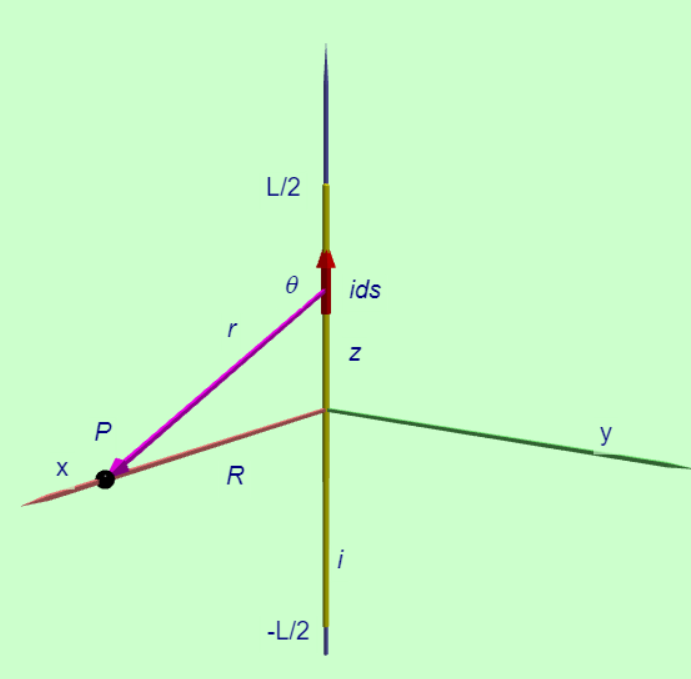 Biot-Savart定律給出一小段電流在空間中所產生的磁場,利用這個定律我們可以來計算一個長直的導線電流在空間中所產生的磁場。在右圖中我們先考慮一小段電流\(id\vec{s}\)在\(P\)點所貢獻的磁場。\(P\)點到達電流導線的垂直距離是\(R\),電流的\(id\vec{s}\)與\(P\)點的距離\(r\),線段與電流導線的夾角是\(\theta\),根據右手定則我們得到電流元素\(id\vec{s}\)所貢獻的磁場\(d\vec{B}\)的方向指向紙面內部,利用積分我們可以得到長直導線電流在\(P\)點的磁場。下面是整個積分的推導過程。
由於線段是直的,我們使用卡氏坐標系。我們將沿z軸對稱放置導線,使場點位於 xy平面內。我們選擇\(P\)點坐落在x軸上,以簡化我們的計算。\(id\vec{s}\)是\(z 和 z + d z\)之間的一個無窮小元素。
\begin{align*}
微量電流元素向量:\amp d\vec s = dz \hat k \\
微量電流元素至點P的向量:\amp \vec r = R \hat i - z \hat k \\
微量電流元素至點P的距離:\amp r = \sqrt{R^2 + z^2 } \\
微量電流元素至點P的單位向量:\amp \hat r = \dfrac{1}{\sqrt{R^2 + z^2 } } \left( R \hat i - z \hat k \right)
\end{align*}
注意,\(\hat{k} \times \hat{k}=0,\quad \text{Biot-Savart定律中的向量外積:}\),
\begin{equation*}
d\vec s \times \hat r = dz \hat k \times \dfrac{1}{\sqrt{R^2 + z^2 } } \left( R \hat i - z \hat k \right) =
\dfrac{R dz}{\sqrt{R^2 + z^2 } }\, \hat j.
\end{equation*}
有了上面的關係式,我們可以依據Biot-Savart定律將微量電流在\(P\)點所貢獻的磁場表示如下(\(注意:\hat{k} \times \hat{k}=0\),):
\begin{equation*}
d\vec{B}_P = \dfrac{\mu_0 i}{4\pi} \, \dfrac{d\vec{s} \times \hat{r}}{r^2} = \dfrac{\mu_0 i}{4\pi}\, \dfrac{R dz}{\left(R^2 + z^2\right)^{3/2} }\, \hat j.
\end{equation*}
最後透過從\(z = - L / 2 至 z = L / 2\)的積分我們可以得到所有電流對磁場的貢獻。由於被積分函數是 \(z\) 的偶函數,並且積分範圍對\(z=0\)對稱,因此從\(z = 0 到 z = L / 2\)積分值的兩倍就是我們要算的積分。
\begin{equation*}
\vec{B}=\int_{\text{circuit}} d\vec B = \int_{\text{circuit}} \dfrac{\mu_0 i}{4\pi}\, \dfrac{R dz}{\left(R^2 + z^2\right)^{3/2} }\, \hat j= 2 \dfrac{\mu_0 i}{4\pi} \int_0^{L/2} \dfrac{R dz}{\left(R^2 + z^2\right)^{3/2} }\, \hat j
\end{equation*}
選擇x軸上的場點使我們的磁場方向朝向正y軸。可以證明,如果選擇正y軸上的場點,將獲得負x軸方向。任意點的方向將是圓柱坐標系\(\hat{\phi}=-\sin \phi \hat{i} + \cos \phi \hat{j}\)單位向量,此向量位在xy平面,磁場將沿圓形路徑轉圈,在圓的切線方向上。可以使用右手定則,拇指的方向指向電流的方向,彎曲四指旋轉的方向就是磁場的方向。
Biot-Savart定律給出一小段電流在空間中所產生的磁場,利用這個定律我們可以來計算一個長直的導線電流在空間中所產生的磁場。在右圖中我們先考慮一小段電流\(id\vec{s}\)在\(P\)點所貢獻的磁場。\(P\)點到達電流導線的垂直距離是\(R\),電流的\(id\vec{s}\)與\(P\)點的距離\(r\),線段與電流導線的夾角是\(\theta\),根據右手定則我們得到電流元素\(id\vec{s}\)所貢獻的磁場\(d\vec{B}\)的方向指向紙面內部,利用積分我們可以得到長直導線電流在\(P\)點的磁場。下面是整個積分的推導過程。
由於線段是直的,我們使用卡氏坐標系。我們將沿z軸對稱放置導線,使場點位於 xy平面內。我們選擇\(P\)點坐落在x軸上,以簡化我們的計算。\(id\vec{s}\)是\(z 和 z + d z\)之間的一個無窮小元素。
\begin{align*}
微量電流元素向量:\amp d\vec s = dz \hat k \\
微量電流元素至點P的向量:\amp \vec r = R \hat i - z \hat k \\
微量電流元素至點P的距離:\amp r = \sqrt{R^2 + z^2 } \\
微量電流元素至點P的單位向量:\amp \hat r = \dfrac{1}{\sqrt{R^2 + z^2 } } \left( R \hat i - z \hat k \right)
\end{align*}
注意,\(\hat{k} \times \hat{k}=0,\quad \text{Biot-Savart定律中的向量外積:}\),
\begin{equation*}
d\vec s \times \hat r = dz \hat k \times \dfrac{1}{\sqrt{R^2 + z^2 } } \left( R \hat i - z \hat k \right) =
\dfrac{R dz}{\sqrt{R^2 + z^2 } }\, \hat j.
\end{equation*}
有了上面的關係式,我們可以依據Biot-Savart定律將微量電流在\(P\)點所貢獻的磁場表示如下(\(注意:\hat{k} \times \hat{k}=0\),):
\begin{equation*}
d\vec{B}_P = \dfrac{\mu_0 i}{4\pi} \, \dfrac{d\vec{s} \times \hat{r}}{r^2} = \dfrac{\mu_0 i}{4\pi}\, \dfrac{R dz}{\left(R^2 + z^2\right)^{3/2} }\, \hat j.
\end{equation*}
最後透過從\(z = - L / 2 至 z = L / 2\)的積分我們可以得到所有電流對磁場的貢獻。由於被積分函數是 \(z\) 的偶函數,並且積分範圍對\(z=0\)對稱,因此從\(z = 0 到 z = L / 2\)積分值的兩倍就是我們要算的積分。
\begin{equation*}
\vec{B}=\int_{\text{circuit}} d\vec B = \int_{\text{circuit}} \dfrac{\mu_0 i}{4\pi}\, \dfrac{R dz}{\left(R^2 + z^2\right)^{3/2} }\, \hat j= 2 \dfrac{\mu_0 i}{4\pi} \int_0^{L/2} \dfrac{R dz}{\left(R^2 + z^2\right)^{3/2} }\, \hat j
\end{equation*}
選擇x軸上的場點使我們的磁場方向朝向正y軸。可以證明,如果選擇正y軸上的場點,將獲得負x軸方向。任意點的方向將是圓柱坐標系\(\hat{\phi}=-\sin \phi \hat{i} + \cos \phi \hat{j}\)單位向量,此向量位在xy平面,磁場將沿圓形路徑轉圈,在圓的切線方向上。可以使用右手定則,拇指的方向指向電流的方向,彎曲四指旋轉的方向就是磁場的方向。如果考慮以電流導線為軸心,\(R\)為半徑的圓週上各點,根據對稱我們知道磁場的方向會沿著圓的切線方向,其大小均相同與\(P\)點的磁場的大小相同。就微量電流元素\(id\vec{s}\)而言,其貢獻的磁場與距離的平方成反比\(dB \propto 1/r^2\),與庫侖定律的平方反比定律相同。積分\(dB\)的結果顯示,一直線電流貢獻的磁場與距離成反比\(B \propto 1/r\),這個結果與直線電荷所產生的電場與距離行為一樣\(E \propto 1/r \)。我們在下面還會回到這個問題上,利用安培定律來考慮磁場的線積分,與封閉曲線所包住的電流總數之間的關係。類似於電場問題的高斯定律,我們可以利用安培定律快速地推導長直導線電流的磁場公式:\(B=\dfrac{\mu_0 i}{2 \pi R}\)。
電流環的磁場
YC-Biot-Savart-loop-i.png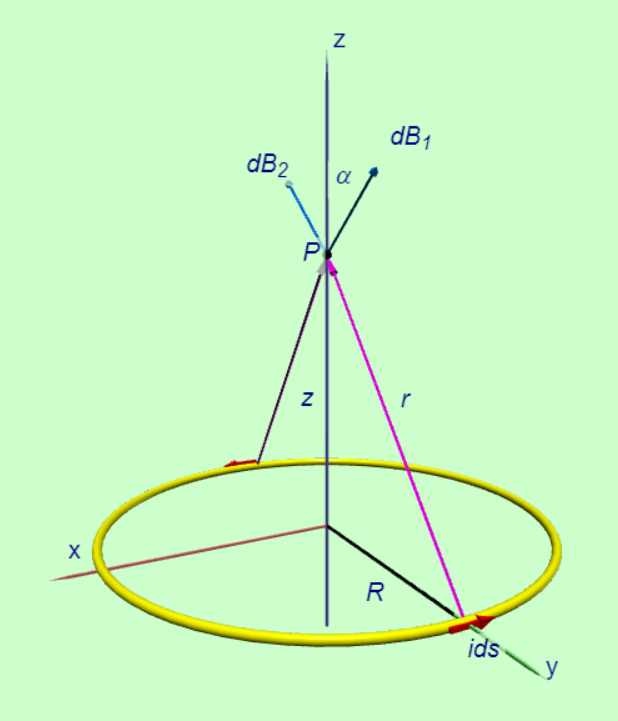 同樣的我們可以利用Biot-Savart定律來計算一個電流環所產生的磁場。我們所要考慮的\(P\)點位在電流環的中央軸上,距離圓環的圓圓心\(z\)的距離,電流環的半徑是\(R\)電流的大小是\(i\)。我們考慮圖形中在\(P_1\)的一小段電流\(ids\)在\(P\)點所貢獻的磁場。根據右手定則我們不難發現,這一小段電流所產生的磁場\(d\vec{B}_2\)如圖形所示,同時具有z方向和y方向的磁場分量。如果我們考慮的\(P_1\)的對稱點\(P_2\)的微量電流單元所貢獻的磁場,會得到圖形中\(d\vec{B}_2\)的貢獻。這兩個磁場貢獻在y方向的磁場分量大小相等,方向相反,因此會互相抵銷。所以這兩個對稱電流貢獻的磁場一定指向\(+z\)軸的方向。以此類推,我們知道整個電流環在\(P\)點所貢獻的磁場必然是在z軸方向。整個公式的推導如下。
同樣的我們可以利用Biot-Savart定律來計算一個電流環所產生的磁場。我們所要考慮的\(P\)點位在電流環的中央軸上,距離圓環的圓圓心\(z\)的距離,電流環的半徑是\(R\)電流的大小是\(i\)。我們考慮圖形中在\(P_1\)的一小段電流\(ids\)在\(P\)點所貢獻的磁場。根據右手定則我們不難發現,這一小段電流所產生的磁場\(d\vec{B}_2\)如圖形所示,同時具有z方向和y方向的磁場分量。如果我們考慮的\(P_1\)的對稱點\(P_2\)的微量電流單元所貢獻的磁場,會得到圖形中\(d\vec{B}_2\)的貢獻。這兩個磁場貢獻在y方向的磁場分量大小相等,方向相反,因此會互相抵銷。所以這兩個對稱電流貢獻的磁場一定指向\(+z\)軸的方向。以此類推,我們知道整個電流環在\(P\)點所貢獻的磁場必然是在z軸方向。整個公式的推導如下。我們注意到這個問題的幾個簡化特徵:
- 這個問題有一個有用的對稱性:環的所有點與場點\(P\)的距離相等。
- 由於環上任一點的電流方向都是沿圓的切線,所以任何電流單元內的電流方向與電流單元到場點\(P\)的方向垂直,夾角是\(90^{\circ}\)。
,在這個特殊情況下磁場的大小為 \[B_c= \dfrac{\mu_0 i}{2 R} \] 磁場的方向也是指向\(+z\)的方向。
如果我們直接用Biot-Savart定律,考慮電流還在\(C\)的磁場貢獻,計算上非常簡單,因為所有電流環微量電流單元與位置向量的外積只有+z軸的磁場分量,因此我們可以很快的得到\(B_c\): \[B_c=\dfrac{\mu_0 i}{4 \pi} \dfrac{2\pi R}{R^2}=\dfrac{\mu_0 i}{2 R} \] 我們在前面的討論已經定義了磁偶極,一個電流環就是最基本的磁偶極,磁偶極矩的大小為\(\mu=iA=i (\pi R^2)\), \begin{equation} B_P =\frac{\mu_0 \mu}{2 \left( R^2 + z^2 \right)^{3/2}} \end{equation}
磁場的磁力線
|
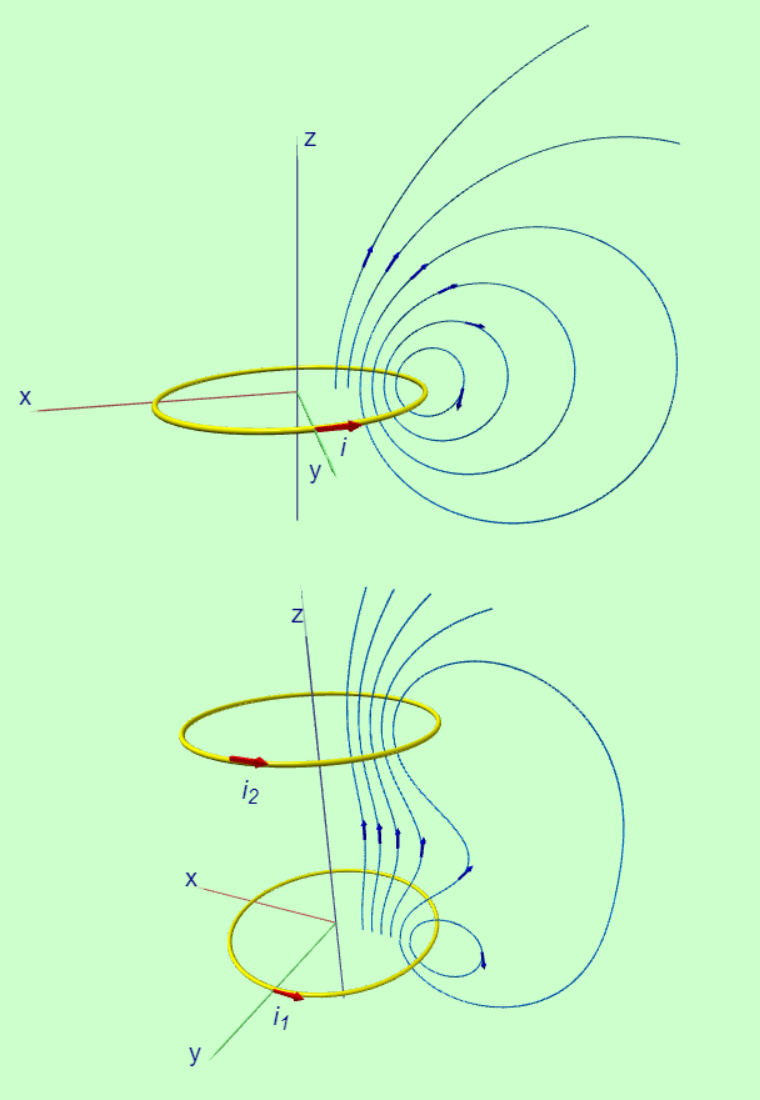
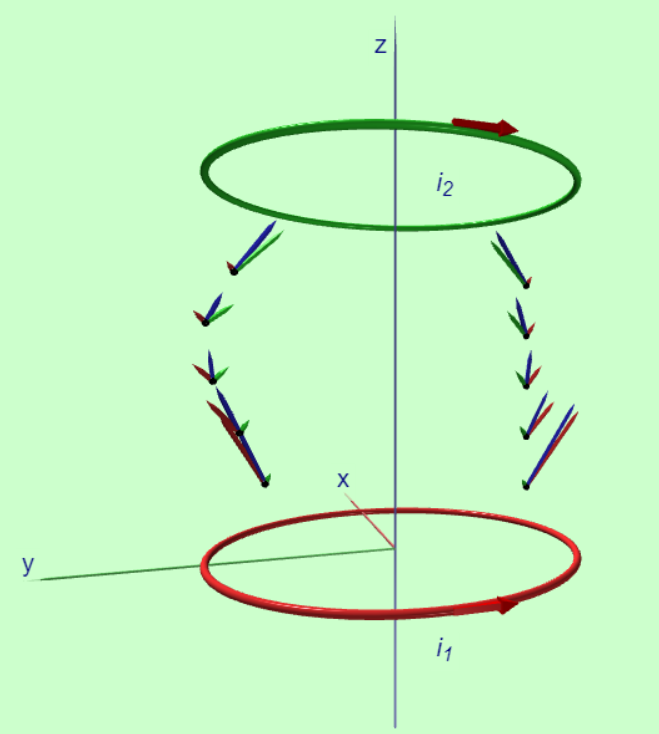
磁場和電場一樣是一種隱藏在空間中的分佈,電場的存在會對帶電粒子產生一個電力的作用,如果我們在空間中擺設許多的電偶極,那麼電偶極矩依循電力的方向耳排列,就能夠讓電力線現形。磁場的存在雖然不能對靜態的電荷施力,但是如果電荷在空間中運動,在有磁場的空間中就會有磁力的作用,因此我們也可以在空間中根據磁場的大小與方向定義磁場的流線。同樣的我們也可以在空間中擺設許多的磁偶極,藉由磁偶極轉動的方向,可具體化磁力線。 對於單一一個電流環我們已經計算出在中央對稱軸上的磁場方向始終指向+z,所以我們知道至少在電流環的中央軸上是一條直線,在偏離中央軸的場點,磁力線的行為就必須再度使用Biot-Savart定律的積分來運算磁場向量。失去對稱的解析計算是非常困難而複雜的計算過程,我們不可能在普通物理的課程中做這樣的計算,但是我們可以利用計算機的數值計算能力來幫助我們計算出偏離開中心軸的磁力線。為了完成這個計算我們寫下一個VPYTHON程式,如下面的連結所呈現的,我們不僅可以做數值計算還可以將計算的結果視覺化,用三維(3D)立體圖形顯示出,電流環在空間的位置和擺設的方向,電流環所產生的磁場與磁力線描繪出來的樣貌 右圖上顯示了一個電流環在空間中所產生的磁力線,其方向大致上是從圓環的中央發出,然後向右轉再從電流環的下方回到出發點,因此磁力線形成一個封閉的曲線。在前面我們提到自然界到目前為止沒有找到磁單極,因此封閉的磁力線的特色與這個結果是一致的。 glowscript:一個電流環的磁力線 右圖中為我們呈現了兩個電流環平行放置,中心軸在同一直線上,圓心相隔一段有限長度的距離。我們可以看到磁力線從下電流環的中央區域發出指向上電流環,在中央地帶我們發現磁力線會向外側彎曲,造成磁力線的密度下降,代表磁場的大小變弱。在幾何形狀上這個磁場形成了我們在上一章所提到的磁瓶子的幾何結構。在上一章中我們已經討論過,帶電粒子在這樣的磁瓶子的磁場中運動,除了會進行螺旋曲線的路徑之外,還會在兩個圓環之間來回震盪,這種磁場的結構有很好的應用,我們地球的磁場就是在地表上空的太空中,形成磁瓶子捕捉太陽輻射出的高能量帶電粒子,避免高能量的粒子直接襲擊地表。除此之外我們也利用磁瓶子限制高能量、高速運動的帶點粒子在有限的空間中,使高速帶電粒子有機會形成對撞,而發生核融合現象,科學家現正積極地使用這種方法為我們未來的能源提供好的解決方案。 glowscript:2電流環的磁力線 在右圖下我們呈現兩個電流環各自在場點所貢獻的磁場,計算的法則當然是Biot-Savart定律。下電流環所貢獻的磁場以紅色箭頭表示,上電流環所貢獻的磁場以綠色的箭頭表示,兩個磁場的和以藍色的箭頭顯示。從圖形中我們可以看見當場點是在兩個環的中點地帶,兩個磁場互相抵消,磁場的強度變小並且磁場的方向向外彎曲,這個計算的結果在佐證上圖中磁瓶子的磁力線是根據基本的Biot-Savart定律的計算得到。 glowscript:2電流環的Biot-Savart計算 |
|
例題
Find the current in a long straight wire that would produce a magnetic field twice the strength of the Earth's at a distance of 5.0 cm from the wire. The Earth's field is about \(5.0 \times 10^{-5}\) T.
\[B=\dfrac{\mu_0 i}{2 \pi r}; \Rightarrow i=\dfrac{2\pi r B}{\mu_0}=\dfrac{2\pi(5.0\times 10^{-2})(1.0 \times 10^{-4})}{4\pi \times 10^{-7}}=25 \, \text{A}\]
\[B=\dfrac{\mu_0 i}{2 \pi r}; \Rightarrow i=\dfrac{2\pi r B}{\mu_0}=\dfrac{2\pi(5.0\times 10^{-2})(1.0 \times 10^{-4})}{4\pi \times 10^{-7}}=25 \, \text{A}\]
例題
What is the field inside a 2.00-m-long solenoid that has 2000 loops and carries a 1600-A current?
\[n=\dfrac{N}{l}=\dfrac{2000}{2}=1000\] \[B=\mu_0 n i=(4\pi \times 10^{-7})(1000)(1600)=2.01\,\text{T}\]
\[n=\dfrac{N}{l}=\dfrac{2000}{2}=1000\] \[B=\mu_0 n i=(4\pi \times 10^{-7})(1000)(1600)=2.01\,\text{T}\]
例題(HL-SP-29-02)
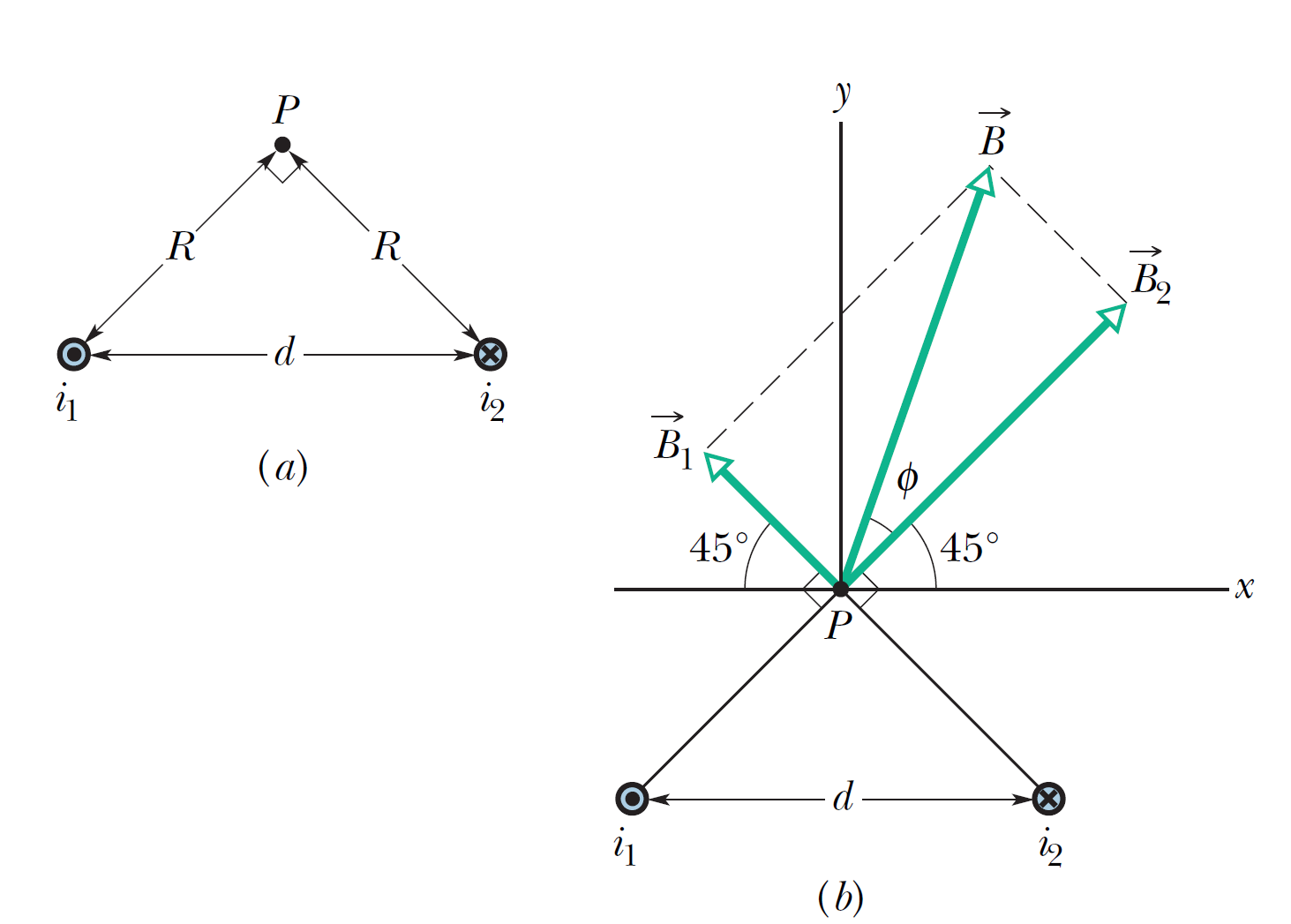 The figure shows two long parallel wires carrying currents \(i_1\) and \(i_2\) in opposite directions. What are the magnitude and direction of the net magnetic field at point \(P\)? Assume the following values: \(i_1= 15\) A, \(i_2= 32\) A, and \(d = 5.3\) cm.
The figure shows two long parallel wires carrying currents \(i_1\) and \(i_2\) in opposite directions. What are the magnitude and direction of the net magnetic field at point \(P\)? Assume the following values: \(i_1= 15\) A, \(i_2= 32\) A, and \(d = 5.3\) cm.該圖顯示了兩條長平行線,它們以相反的方向承載電流 \(i_1\) 和 \(i_2\)。 點 \(P\) 處的淨磁場的大小和方向是多少? 假設以下值:\(i_1= 15\) A、\(i_2= 32\) A 和 \(d = 5.3\) cm。
\[B_1=\dfrac{\mu_0 i_1}{2 \pi R} \quad \text{and} \quad B_2={\mu_0 i_2}{2 \pi R}; \quad R=d \cos 45^{\circ}\] \[B=\sqrt{B_1^2 + B_2^2}=\dfrac{\mu_0}{2\pi d \cos 45^{\circ}}\sqrt{i_1^2+i_2^2}=1.89 \times 10^{-4} \, \text{T}\] The angle between the directions of \(\vec{B} \text{ and } \vec{B}_2\): \[\phi=\tan^{-1} \dfrac{B_1}{B_2}=\tan^{-1} \dfrac{i_1}{i_2}=25^{\circ}\] The angle between the directions of \(\vec{B} \text{ and } +x:\) \[\Phi+ 45^{\circ}=70^{\circ} \]
磁場安培定律
 Ampere 對 Biot 和 Savart 的工作提出了一些反對意見。例如,他覺得他們的實驗不夠精確,不足以讓他們確定\(\sin \theta\)因子確實需要。他對他們使用“電流元素”感到不舒服,因為不存在孤立的電流元素。\(ids\)始終是完整電路的一部分。因此,他進行了自己的實驗和理論研究,並獲得了電流與其產生的磁場之間的不同關係,現在稱為安培定律。雖然安培定律可以從Biot-Savart的\(d\vec{B}\)表達式導出,但我們不打算這樣做。相對地,我們可以通過考慮一無限直導線電流所產生的磁場來說明安培定律的合理性。我們知道場線是同心圓,並且磁場的大小是\(B=\dfrac{\mu_0 i}{2 \pi r}\),這個公式又可以寫成
\[B (2 \pi r)= \mu_0 i\]
上式左邊可以看成是磁場對一個圓做路徑積分,因為磁場的方向與圓的切線方向重疊,因此對封閉的路徑進行路徑積分的結果等於是磁場\(B\)乘以圓周長\(2\pi r\)。上式右邊是這個封閉的路徑所包含的電流總量\(i_{enc}\)與\(\mu_0\)的乘積,基本上這就是安培定律的一個特例。廣義的安培定律所選擇的封閉路徑不需要是一個圓,即使是一個圓也不需要把電線放在圓心。只要對封閉的路徑上的磁場進行路徑積分,必然會等於封閉路徑所包含(enclosed, enc)的電流總量與\(\mu_0\)的乘積,
\[ \oint_C \vec{B} \cdot d\vec{s} = \mu_0 i_{\text{enc}}\]
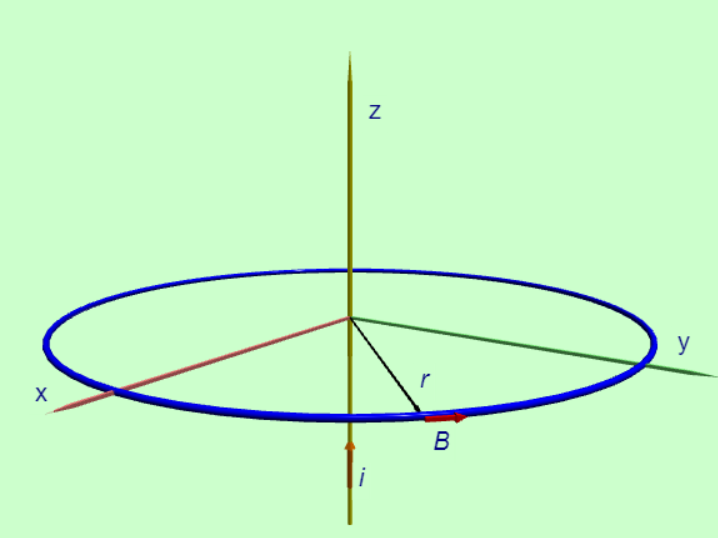
更明確的說,安培環所包住的電流\(i_{enc}\)就是通過安培環所決定的曲面的電流總量,對於那些在安培環附近但是並未穿過曲面的電流而言,並不計入安培定律的電流當中。對於任意一個安培環,只要這個電流不在這個環當中,我們總是可以把這樣的封閉路徑做適當的切割,讓每一個小的環都類似於右圖的結構。每一個小的環對路徑積分的貢獻是零,整體而言任何一個環,只要電流沒有穿過這個環,路徑積分的結果就是零,這就說明了安培定律右邊的電流為何只計算穿過安培環的電流總量。
Ampere 對 Biot 和 Savart 的工作提出了一些反對意見。例如,他覺得他們的實驗不夠精確,不足以讓他們確定\(\sin \theta\)因子確實需要。他對他們使用“電流元素”感到不舒服,因為不存在孤立的電流元素。\(ids\)始終是完整電路的一部分。因此,他進行了自己的實驗和理論研究,並獲得了電流與其產生的磁場之間的不同關係,現在稱為安培定律。雖然安培定律可以從Biot-Savart的\(d\vec{B}\)表達式導出,但我們不打算這樣做。相對地,我們可以通過考慮一無限直導線電流所產生的磁場來說明安培定律的合理性。我們知道場線是同心圓,並且磁場的大小是\(B=\dfrac{\mu_0 i}{2 \pi r}\),這個公式又可以寫成
\[B (2 \pi r)= \mu_0 i\]
上式左邊可以看成是磁場對一個圓做路徑積分,因為磁場的方向與圓的切線方向重疊,因此對封閉的路徑進行路徑積分的結果等於是磁場\(B\)乘以圓周長\(2\pi r\)。上式右邊是這個封閉的路徑所包含的電流總量\(i_{enc}\)與\(\mu_0\)的乘積,基本上這就是安培定律的一個特例。廣義的安培定律所選擇的封閉路徑不需要是一個圓,即使是一個圓也不需要把電線放在圓心。只要對封閉的路徑上的磁場進行路徑積分,必然會等於封閉路徑所包含(enclosed, enc)的電流總量與\(\mu_0\)的乘積,
\[ \oint_C \vec{B} \cdot d\vec{s} = \mu_0 i_{\text{enc}}\]
更明確的說,安培環所包住的電流\(i_{enc}\)就是通過安培環所決定的曲面的電流總量,對於那些在安培環附近但是並未穿過曲面的電流而言,並不計入安培定律的電流當中。對於任意一個安培環,只要這個電流不在這個環當中,我們總是可以把這樣的封閉路徑做適當的切割,讓每一個小的環都類似於右圖的結構。每一個小的環對路徑積分的貢獻是零,整體而言任何一個環,只要電流沒有穿過這個環,路徑積分的結果就是零,這就說明了安培定律右邊的電流為何只計算穿過安培環的電流總量。
安培定律
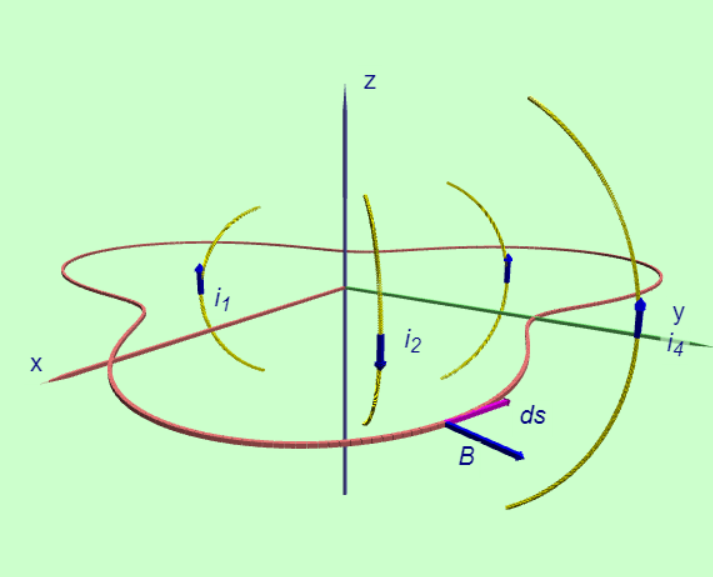 右圖顯示任意一個封閉路徑以及流進與流出頁面的電流。對於沿路徑的無窮小位移\(d\vec{s}\) 的路徑積分:
\[ \vec{B} \cdot d\vec{s}= B ds \cos \theta\]
根據安培定律,該乘積在閉合路徑周圍的總和(積分)為\(\mu_0 i_{enc}\)
其中 \(i_{enc}\)\)是流過路徑所包圍的表面的淨電流。在計算路徑積分的方向(順時針或逆時針)由右手給出規則:當右手拇指指向電流時,捲曲的手指表示沿路徑的正方向。安培定律的公式僅適用於穩定電流(並非隨著時間改變的動態電流)和非磁性材料,例如銅(Cu)。封閉的電流不必流入一根導線;一束帶電粒子也構成電流。安培定律中出現的B是由於附近的所有電流,而不僅僅是路徑所包圍的電流。為了用安培定律確定磁場,電流的幾何形狀必須具有足夠的對稱性,以便可以輕鬆地完成積分的計算。這個在應用上考量的情況和靜電學當中的高斯定律的應用非常類似,我們必須先分析電場的大小與方向在空間中的分佈概況,再選擇適當的高斯面一樣。我們必須先根據電流的結構,分析磁場的大小與方向在空間中的分佈和對稱性,然後才能做出合適的封閉路徑(安培環)的選擇。安培定律的公式如下:
\[ \oint_C \vec{B} \cdot d\vec{s} = \mu_0 i_{\text{enc}}\]
右圖顯示任意一個封閉路徑以及流進與流出頁面的電流。對於沿路徑的無窮小位移\(d\vec{s}\) 的路徑積分:
\[ \vec{B} \cdot d\vec{s}= B ds \cos \theta\]
根據安培定律,該乘積在閉合路徑周圍的總和(積分)為\(\mu_0 i_{enc}\)
其中 \(i_{enc}\)\)是流過路徑所包圍的表面的淨電流。在計算路徑積分的方向(順時針或逆時針)由右手給出規則:當右手拇指指向電流時,捲曲的手指表示沿路徑的正方向。安培定律的公式僅適用於穩定電流(並非隨著時間改變的動態電流)和非磁性材料,例如銅(Cu)。封閉的電流不必流入一根導線;一束帶電粒子也構成電流。安培定律中出現的B是由於附近的所有電流,而不僅僅是路徑所包圍的電流。為了用安培定律確定磁場,電流的幾何形狀必須具有足夠的對稱性,以便可以輕鬆地完成積分的計算。這個在應用上考量的情況和靜電學當中的高斯定律的應用非常類似,我們必須先分析電場的大小與方向在空間中的分佈概況,再選擇適當的高斯面一樣。我們必須先根據電流的結構,分析磁場的大小與方向在空間中的分佈和對稱性,然後才能做出合適的封閉路徑(安培環)的選擇。安培定律的公式如下:
\[ \oint_C \vec{B} \cdot d\vec{s} = \mu_0 i_{\text{enc}}\]
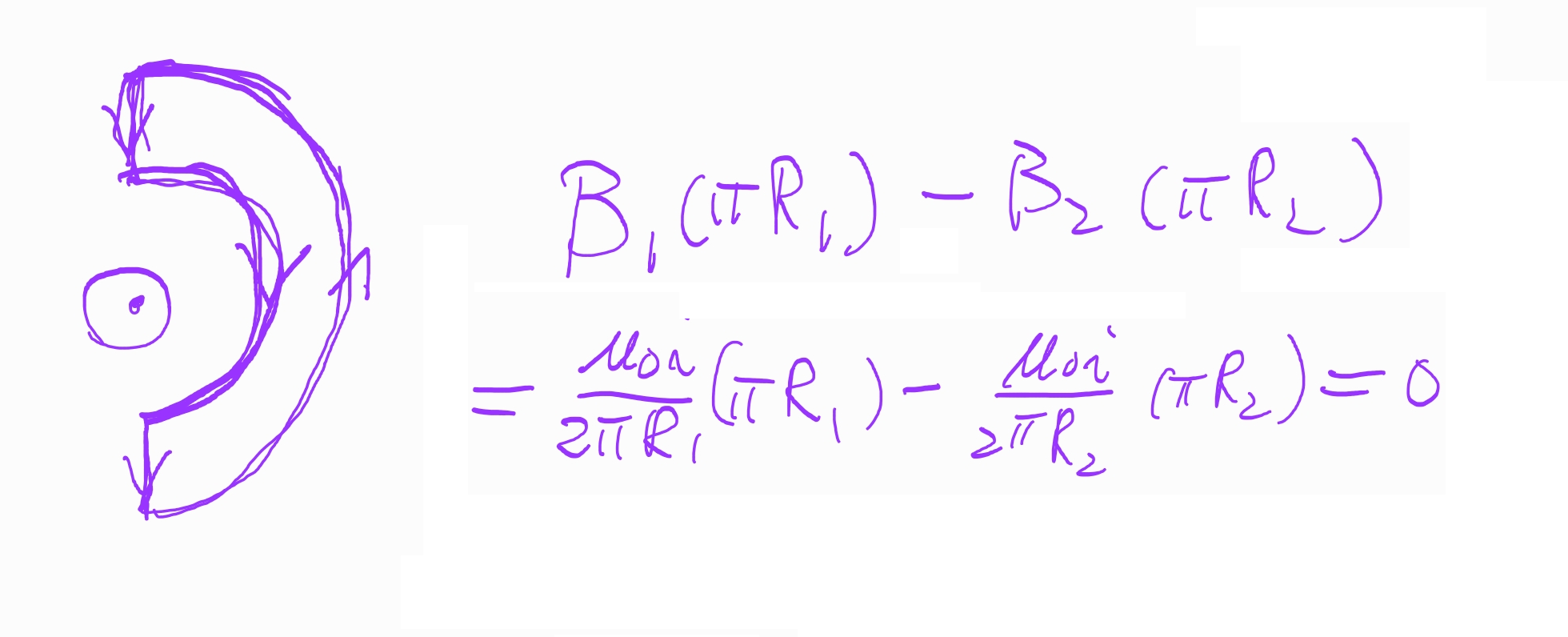 在安培環附近沒有穿過安培環曲面的電流,當然也會在安培環的路徑上有磁場的貢獻,但是經過一個封閉迴路的積分之後,這些磁場的貢獻會相互抵銷,使得路徑積分的總體貢獻為0,因此這些電流不需要放進右側的電流計算當中。如右圖所示,如果我們選擇一個安培環未包含無限長的導線電流,當我們對這個安培環的磁場作路徑積分的計算時,我們可以非常清楚的觀察到,外圍半圓的路徑積分貢獻與內側半圓的路徑積分互相抵消,而直線部分,因為路徑的方向與磁場方向垂直,沒有路徑積分的貢獻,因此整體路徑積分為0。
在安培環附近沒有穿過安培環曲面的電流,當然也會在安培環的路徑上有磁場的貢獻,但是經過一個封閉迴路的積分之後,這些磁場的貢獻會相互抵銷,使得路徑積分的總體貢獻為0,因此這些電流不需要放進右側的電流計算當中。如右圖所示,如果我們選擇一個安培環未包含無限長的導線電流,當我們對這個安培環的磁場作路徑積分的計算時,我們可以非常清楚的觀察到,外圍半圓的路徑積分貢獻與內側半圓的路徑積分互相抵消,而直線部分,因為路徑的方向與磁場方向垂直,沒有路徑積分的貢獻,因此整體路徑積分為0。
利用安培定律計算螺線管電流產生的磁場
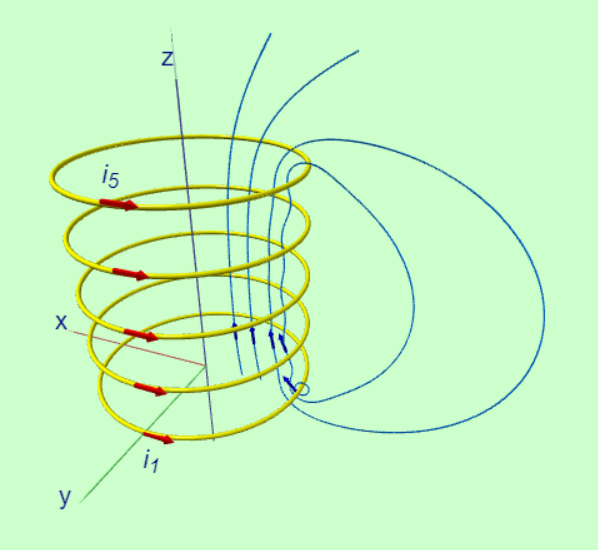 在這個小節中我們要探討電機工程上經常要使用的一種元件叫做螺線管的元件。製備螺旋管的方法很簡單,準備一個圓柱體,在這個圓柱體的外圍纏繞電線就形成了這樣的管狀的電線就叫螺線管。螺線管的主要用途是在產生磁場,從我們上面的討論已經知道,一個電流環會產生磁場圍繞著電流環,如果我們有多個電流環沿著z軸整齊排列,那麼電流電流環所產生的磁場依據線性疊加原則,會隨著電流環的數量增加,而漸次的改變磁場的大小和空間中的方向。在上一個小節中,我們看到兩個電流環所形成的磁力線的結構,就是我們在上個單元所提到的磁瓶子。
在這個小節中我們要探討電機工程上經常要使用的一種元件叫做螺線管的元件。製備螺旋管的方法很簡單,準備一個圓柱體,在這個圓柱體的外圍纏繞電線就形成了這樣的管狀的電線就叫螺線管。螺線管的主要用途是在產生磁場,從我們上面的討論已經知道,一個電流環會產生磁場圍繞著電流環,如果我們有多個電流環沿著z軸整齊排列,那麼電流電流環所產生的磁場依據線性疊加原則,會隨著電流環的數量增加,而漸次的改變磁場的大小和空間中的方向。在上一個小節中,我們看到兩個電流環所形成的磁力線的結構,就是我們在上個單元所提到的磁瓶子。右圖中我們顯示了一個有5個電流環的螺線管,空間中任何一點的磁場都是由這5個電流在該處的磁場貢獻的向量和。這個圖形是利用vpython程式,直接從Biot-Savart定律的計算得到。從磁力線的結構我們可以看出來,在螺線管的內部形成一個方向固定指向正z軸方向的均勻磁場,只有在非常靠近螺線管邊緣處才會有所變化。並且只要螺旋管的圈數不停的增加,電線之間的密度越是緊緻,螺旋管內部的磁場更趨近於均勻的磁場。並且可以觀察到,在螺線管的外側的磁力線非常疏散,表示在螺線管的外側的磁場非常的微弱,因此我們可以預期,當螺線管變長,圈數變得更緊密的極限下,螺線管的電流所產生的磁場在螺線管內部是均勻的磁場,螺線管的外部磁場為零。這個情況和靜電學當中帶有異性電荷的平行電板類似。在兩個板子之間產生均勻的電場,在平行電板的外側電場為0非常相似。這兩個元件也是電子線路當中代表性的兩個元件,平板是電容,螺線管是電感。
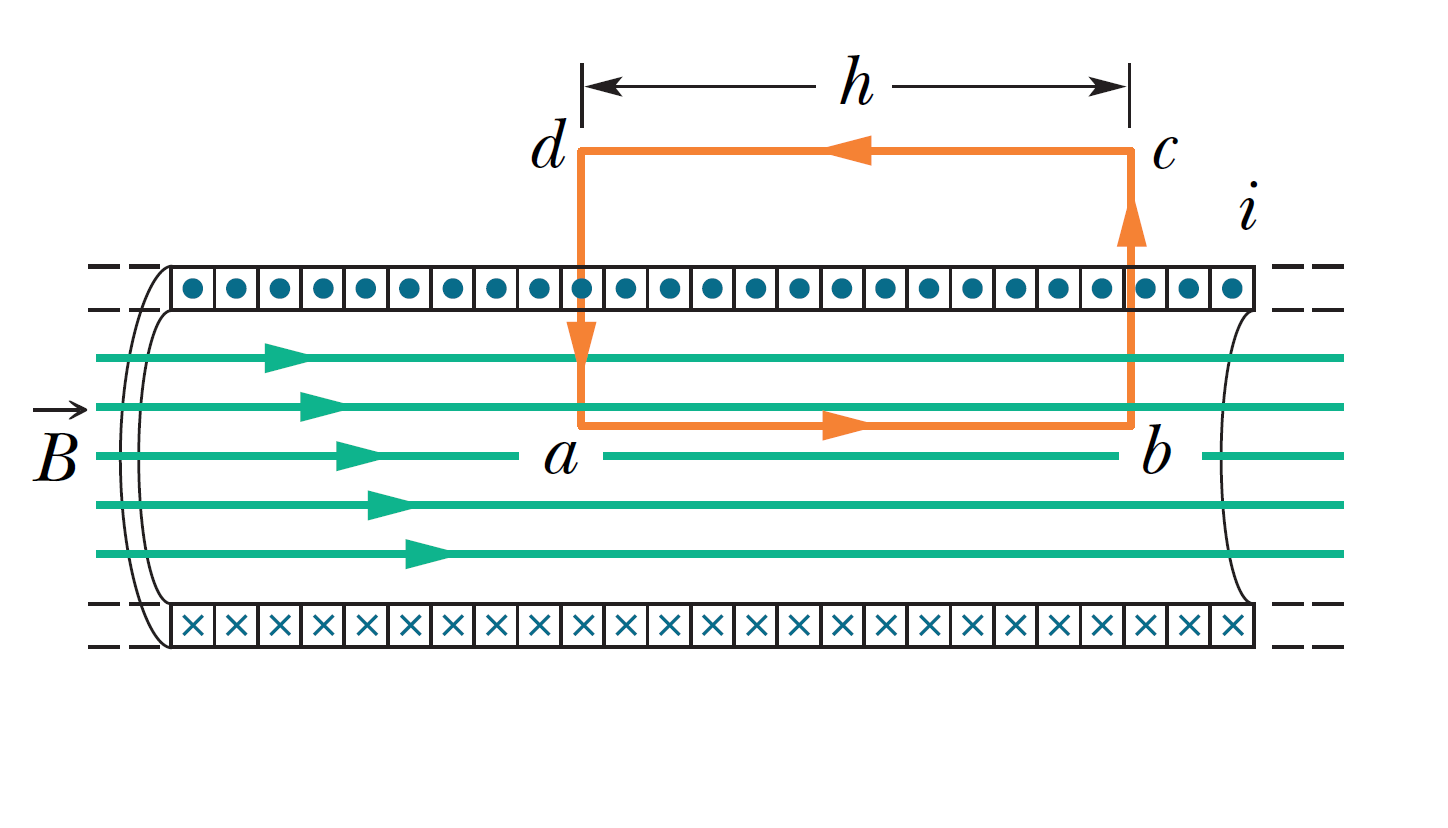 我們現在將注意力轉向安培定律,我們希望能夠從上面對磁場的分析,再利用安培定律來計算螺線管當中的磁場大小。我們假設螺線管的長度\(L\)遠大於直徑\(d=2R\)。
如右圖所示我們假設螺線管當中的線圈總數\(N\),因此我們可以得到單位長度中的電線圈數,也就是圈數密度\(n\)
\[n=\dfrac{N}{L}\]
根據我們上面的討論,可以選擇一個長方形的安培環,如圖所示。長方形的長邊沿著z軸方向,長度為\(h\),寬邊與螺線管垂直,長度為\(w\)。當我們做安培定律的磁場線積分時,發現只有螺線管內部沿著磁場方向的路徑積分有貢獻,其他三個矩形邊的路徑積分貢獻都是0。其中外部的磁場為0,因此沒有貢獻;而沿著寬邊與磁場方向垂直(\(\vec{B} \cdot d\vec{s} = 0\))的路徑做積分,其貢獻一樣為0,所以安培定律左邊的路徑積分結果非常簡單,就是螺線管內部的磁場乘上安培環的長度:\(B h\)。安培定律的右側是關於這個穿過安培環的電流總數。我們知道穿過長方形的總共線圈總數為\(n h\),每一環當中的電流為\(i\),因此安培還所包含的電流總量為\(i_{enc}=n h i\),透過安培定律我們很快的得到螺線管內部的磁場大小如下:
\[B h=\mu_0 n h i\]
\[B=\mu_0 n i \]
我們現在將注意力轉向安培定律,我們希望能夠從上面對磁場的分析,再利用安培定律來計算螺線管當中的磁場大小。我們假設螺線管的長度\(L\)遠大於直徑\(d=2R\)。
如右圖所示我們假設螺線管當中的線圈總數\(N\),因此我們可以得到單位長度中的電線圈數,也就是圈數密度\(n\)
\[n=\dfrac{N}{L}\]
根據我們上面的討論,可以選擇一個長方形的安培環,如圖所示。長方形的長邊沿著z軸方向,長度為\(h\),寬邊與螺線管垂直,長度為\(w\)。當我們做安培定律的磁場線積分時,發現只有螺線管內部沿著磁場方向的路徑積分有貢獻,其他三個矩形邊的路徑積分貢獻都是0。其中外部的磁場為0,因此沒有貢獻;而沿著寬邊與磁場方向垂直(\(\vec{B} \cdot d\vec{s} = 0\))的路徑做積分,其貢獻一樣為0,所以安培定律左邊的路徑積分結果非常簡單,就是螺線管內部的磁場乘上安培環的長度:\(B h\)。安培定律的右側是關於這個穿過安培環的電流總數。我們知道穿過長方形的總共線圈總數為\(n h\),每一環當中的電流為\(i\),因此安培還所包含的電流總量為\(i_{enc}=n h i\),透過安培定律我們很快的得到螺線管內部的磁場大小如下:
\[B h=\mu_0 n h i\]
\[B=\mu_0 n i \]
例題:螺線管內的磁場
What is the field inside a 2.00-m-long solenoid that has 2000 loops and carries a 1600-A current?
一個 2.00 米長、有 2000 個迴路並承載 1600A 電流的螺線管內的磁場是多少?
\[n=\dfrac{N}{l}=\dfrac{2000}{2}=1000\,\text{1/m}\] \[B=\mu_0 n i=2.01 \, \text{A}\]
一個 2.00 米長、有 2000 個迴路並承載 1600A 電流的螺線管內的磁場是多少?
\[n=\dfrac{N}{l}=\dfrac{2000}{2}=1000\,\text{1/m}\] \[B=\mu_0 n i=2.01 \, \text{A}\]
例題:電流均勻分佈的磁場
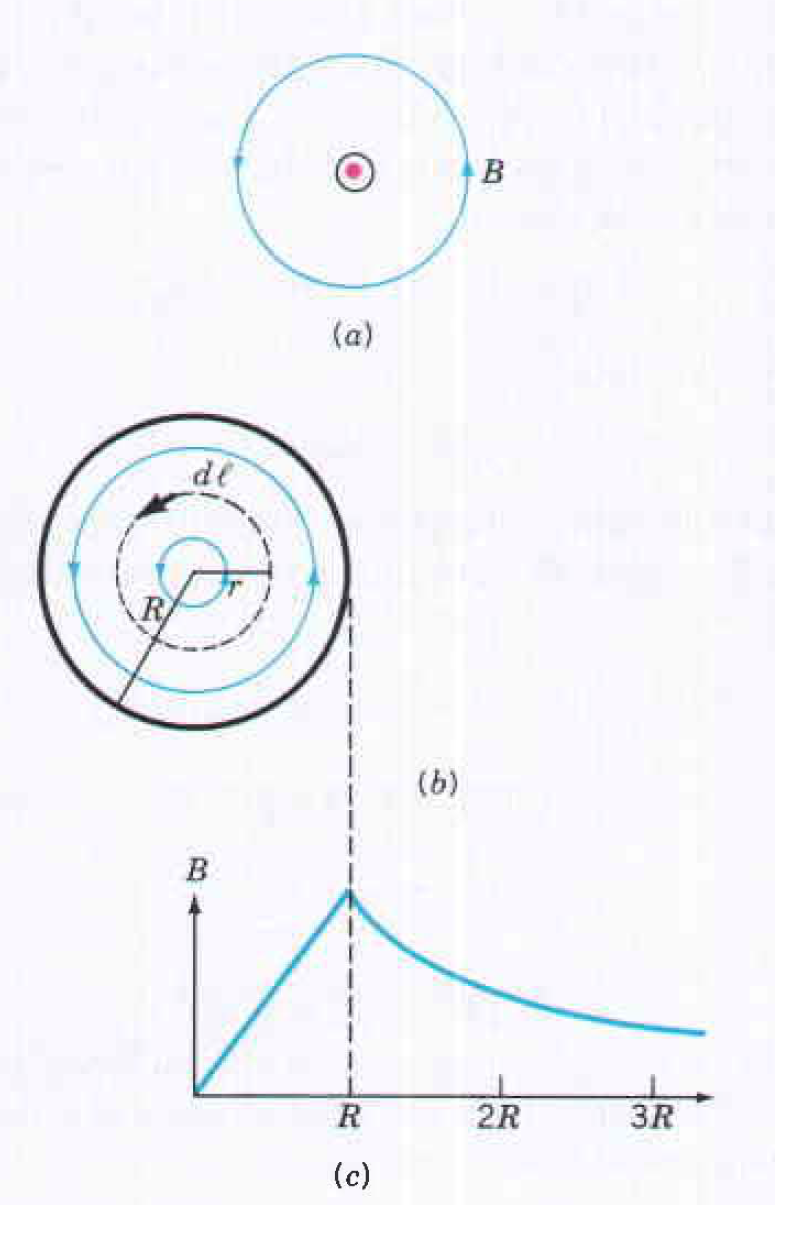 半徑為 \(R\) 的無限直導線承載電流 \(I\)。求 (a) \(r \gt R\) 和 (b) \(r \lt R\) 距離導線中心距離 \(r\) 處的磁場。假設電流均勻分佈在導線的橫截面上。
半徑為 \(R\) 的無限直導線承載電流 \(I\)。求 (a) \(r \gt R\) 和 (b) \(r \lt R\) 距離導線中心距離 \(r\) 處的磁場。假設電流均勻分佈在導線的橫截面上。\(\oint \vec{B} \cdot d\vec{s} = \oint Bds=\mu_0 I \tag{A1} \)
\(B=\dfrac{\mu_0 I}{2 \pi r} \tag{A2} \)
例題(HL-SP-29-03)
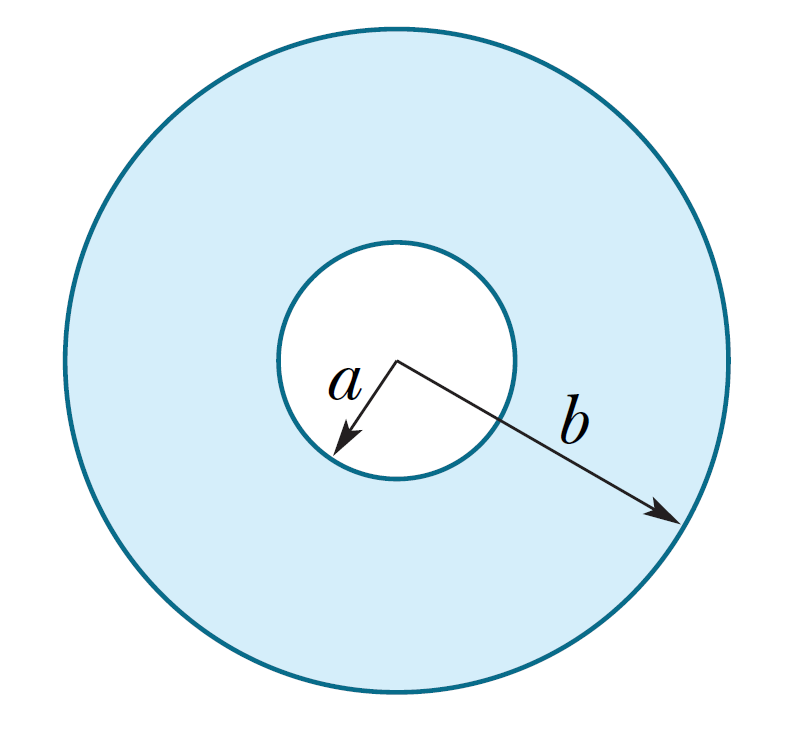 The figure shows the cross section of a long conducting cylinder with inner radius \(a=2.0\) cm and outer radius \(b = 4.0\) cm. The cylinder carries a current out of the page, and the magnitude of the current density in the cross section is given by \(J=c r^2\), with \(c = 3.0 \times 10^6\) A/m4 and r in meters. What is the magnetic field \(\vec{B}\) at a point that is 3.0 cm from the central axis of the cylinder?
The figure shows the cross section of a long conducting cylinder with inner radius \(a=2.0\) cm and outer radius \(b = 4.0\) cm. The cylinder carries a current out of the page, and the magnitude of the current density in the cross section is given by \(J=c r^2\), with \(c = 3.0 \times 10^6\) A/m4 and r in meters. What is the magnetic field \(\vec{B}\) at a point that is 3.0 cm from the central axis of the cylinder? 該圖顯示了一個內半徑為 \(a=2.0\) cm,外半徑為 \(b = 4.0\) cm 的長導電圓柱體的橫截面。 圓柱體將電流帶出頁面,截面內電流密度的大小由 \(J=c r^2\) 給出,其中 \(c = 3.0 \times 10^6\) A/m 4 和 r 以米為單位。 距圓柱中心軸 3.0 cm 處的磁場 \(\vec{B}\) 是多少?
\[ \begin{equation} \begin{split} i_{enc} &=\int J dA =\int_0^r cr^2(2\pi r dr) \\ &2\pi c \int_0^r r^3 dr=2 \pi c\left[ \dfrac{r^4}{4}\right]_a^r \\ &=\dfrac{\pi c (r^4 - a^4)}{2} \end{split} \end{equation} \] \[B(2\pi r)=-\dfrac{\mu_0 \pi c}{2}(r^4 - a^4)\] \[B=-\dfrac{\mu_0 c}{4 r}(r^4 - a^4)=- \dfrac{(4\pi \times 10^{-7})(3 \times 10^6)}{4(0.03)}=-2.0 \times 10^{-5} \, \text{T}\]
例題(HL-SP-29-04):Magnetic Field of a solenoid(螺線管的磁場)
A solenoid has length \(L = 1.23\) m and inner diameter \(d = 3.55\) cm, and it carries a current \(i = 5.57\) A. It consists of five close-packed layers, each with 850 turns along length \(L\). What is \(B\) at its center?
螺線管的長度為 \(L = 1.23\) m,內徑為 \(d = 3.55\) cm,它承載的電流為 \(i = 5.57\) A。它由五個密排層組成,每個層有 850 沿長度 \(L\) 轉動。 在它的中心\(B=?\)
\begin{align*} B &=\mu_0 i n =(4\pi \times 10^{-7})(5.57) \dfrac{5 \times 850}{1.23} \\ &=2.42 \times 10^{-2} \,\text{T} \end{align*}
螺線管的長度為 \(L = 1.23\) m,內徑為 \(d = 3.55\) cm,它承載的電流為 \(i = 5.57\) A。它由五個密排層組成,每個層有 850 沿長度 \(L\) 轉動。 在它的中心\(B=?\)
\begin{align*} B &=\mu_0 i n =(4\pi \times 10^{-7})(5.57) \dfrac{5 \times 850}{1.23} \\ &=2.42 \times 10^{-2} \,\text{T} \end{align*}
例題:Magnetic Field of a Toroid(環形線圈的磁場)
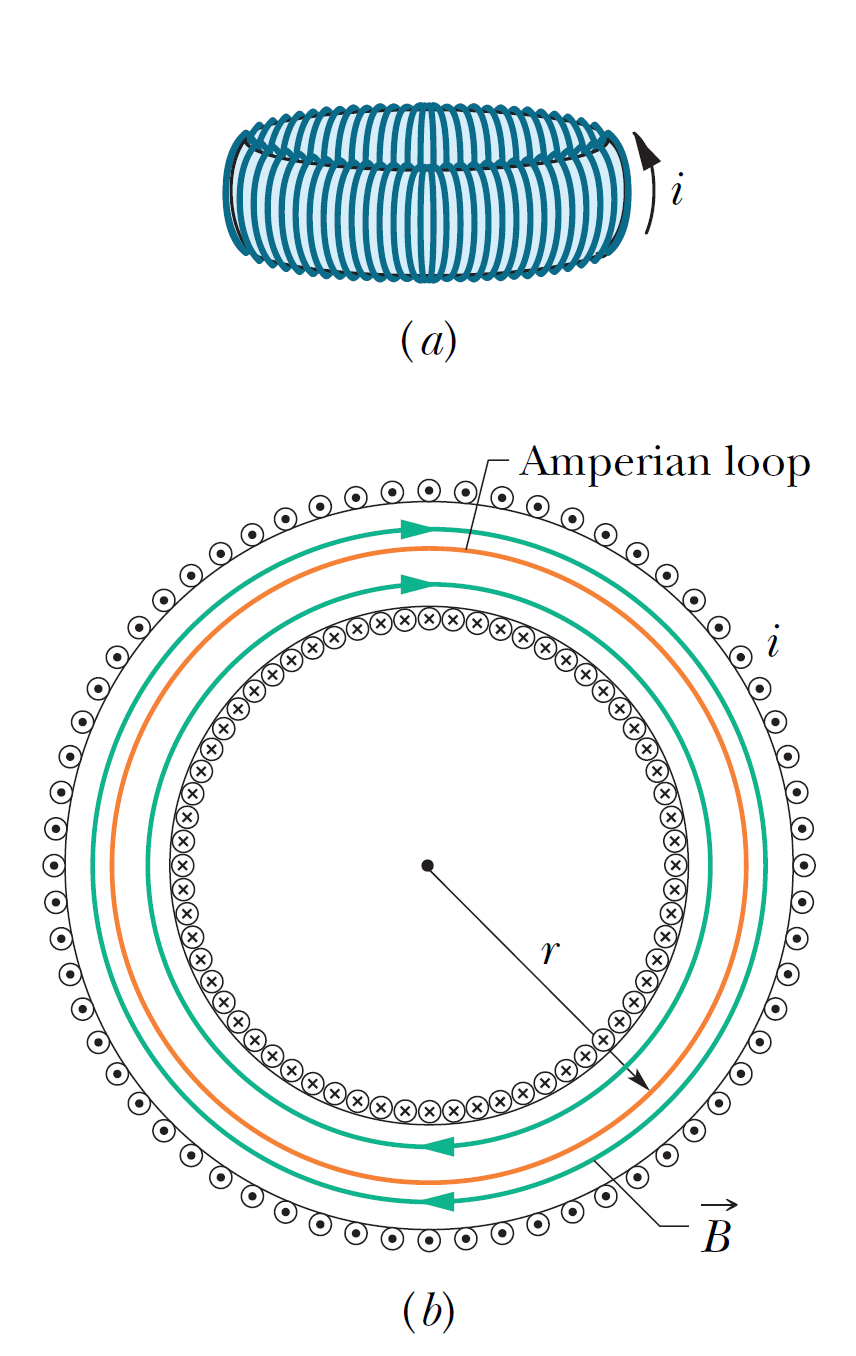 Fig.(a) shows a toroid, which we may describe as a (hollow) solenoid that has been curved until its two ends meet, forming a sort of hollow bracelet. What magnetic field \(\vec{B}\) is set up inside the toroid (inside the hollow of the bracelet)? We can find out from Ampere's law and the symmetry of the bracelet. From the symmetry, we see that the lines of \(\vec{B}\) form concentric circles inside the toroid, directed as shown in Fig.(b) Let us choose a concentric circle of radius \(r\) as an Amperian loop and traverse it in the clockwise direction. Ampere's law yields
\[B(2\pi r)=\mu_0 i N; \quad B=\dfrac{\mu_0 i N}{2\pi} \dfrac{1}{r}\]
\(N\) is the total number of turns. In contrast to the situation for a solenoid, B is not constant over the cross section of a toroid, \(B \propto 1/r\).
Fig.(a) shows a toroid, which we may describe as a (hollow) solenoid that has been curved until its two ends meet, forming a sort of hollow bracelet. What magnetic field \(\vec{B}\) is set up inside the toroid (inside the hollow of the bracelet)? We can find out from Ampere's law and the symmetry of the bracelet. From the symmetry, we see that the lines of \(\vec{B}\) form concentric circles inside the toroid, directed as shown in Fig.(b) Let us choose a concentric circle of radius \(r\) as an Amperian loop and traverse it in the clockwise direction. Ampere's law yields
\[B(2\pi r)=\mu_0 i N; \quad B=\dfrac{\mu_0 i N}{2\pi} \dfrac{1}{r}\]
\(N\) is the total number of turns. In contrast to the situation for a solenoid, B is not constant over the cross section of a toroid, \(B \propto 1/r\). 圖(a)顯示了一個環形線圈,我們可以將其描述為一個(空心)螺線管,該螺線管一直彎曲直到其兩端相遇,形成一種空心手鐲。 計算在環形內部(手鐲的空心內)的磁場 \(\vec{B}\)?
我們可以從安培定律和手鐲的對稱性著手。從對稱性中,我們看到 \(\vec{B}\) 的線在環形內部形成同心圓,方向如圖(b)所示。我們選擇半徑為\(r\)的同心圓作為安培環,並以順時針方向積分。安培定律: \[B(2\pi r)=\mu_0 i N; \quad B=\dfrac{\mu_0 i N}{2\pi} \dfrac{1}{r}\] \(N\)是總圈數。與螺線管的情況相對,磁場\(\vec{B}\)在環形截面上不是恆定的,\(B\propto 1/r\)。
授課教師
陳永忠 ycchen@thu.edu.tw