電感與振盪網路
自感應，自感(電感)
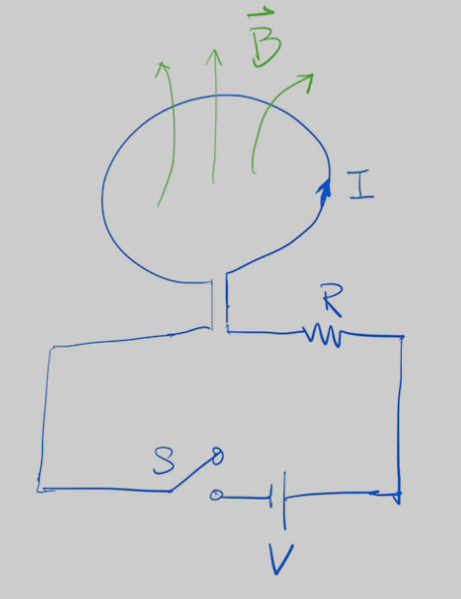如圖所示假如我們將一個圓形線圈接到一個端電壓為V的直流電池，當按下開關S的時候電路接通，線圈上的電流並不會突然由0提升到\(\dfrac{V}{R}\)，這是因為當線圈上的電流開始由0增加時，此電流所產生的磁場，穿過線圈本身的磁通量，也隨時間而增加，這種隨時間增加的磁通量，促成線圈上出現一個會抵制磁通量改變的感應電動勢。這個自我感應的電動在電流增加的過程中，其極性相反於外加的電動勢。因此線圈上的電流是漸次增加到飽和值\(\dfrac{V}{R}\)，而非驟然增加到飽和值。這種在導電線圈上，自我的電磁感應現象稱為自感應。自感應所產生的電動勢顯然正比於線圈上的電流的時間改變率，當線圈是由N圈導線所組成，並且通過每圈導線的磁通量都相等時，自感應電動勢可以寫成
\[\mathscr{E}=-N\dfrac{d\Phi_B}{dt}=-L\dfrac{dI}{dt}\]
在公式中\(I\)是線圈上的電流，\(\Phi_B\)為此電流I所產生的磁場穿過一線圈導線的磁通量，比例常數\(L\)稱為此線圈的自感。一個線圈的自感可由上面的公式的感應電動勢來定義和測量，可以用下面這個公式來作為自感的定義
\[L=\dfrac{N\Phi_B}{I}\]
自感(電感)的單位的單位是亨利，H。
例題：螺線管的自感:
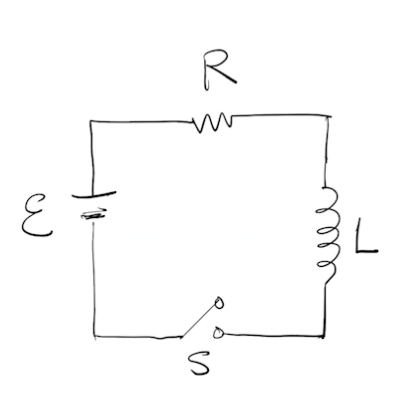考慮一個自感為\(L\)的線圈與一個電阻值為\(R\)的電阻，以及一個電動勢為\(\mathscr{E}\)的直流電池構成的電路，如右圖所示。假設電池的內電阻以及感應線圈的電阻都遠小於\(R\)，可忽略不計。並且假設開關\(S\)按下前，電路上的電流為0。當開關\(S\)在\(t=0\)按下時，電路接通，電流開始增加。同時在感應線圈上出現一個感應電動勢\(\mathscr{E}_L\)對抗電池的電動勢，因為\(\mathscr{E}_L\)對抗\(\mathscr{E}\)，所以又稱為反電動勢。根據電感的定義我們有下列的關係
\[\mathscr{E}_L=-L\dfrac{dI}{dt}\]
利用迴路定理我們可以得到下面關於電位差的公式：
\[\mathscr{E}-IR-L\dfrac{dI}{dt}=0\]
上面的公式稍加整理可以得到如下關於電流\(I\)的微分方程式
\[\dfrac{dI}{dt}+\dfrac{R}{L}I=\dfrac{\mathscr{E}}{L}\]
同樣的，我們不在這邊講解如何求解這個微分方程式，而直接把這個為微分方程式的解直接列出如下的電流函數
\[I(t)=\dfrac{\mathscr{E}}{R}-I_0 e^{-\frac{Rt}{L}}\]
我們知道初始條件\(t=0\)，\(I=0\)，所以我們得到上面公式的\(I_0=\dfrac{\mathscr{E}}{R}\)。因此上面的公式又可以寫成
\[I(t)=\dfrac{\mathscr{E}}{R}[1- e^{-\frac{t}{L/R}}\]
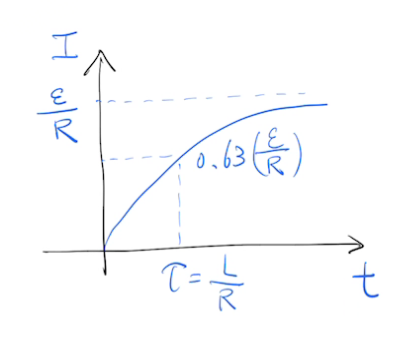其中指數函數的常數\(\tau=L/R\)稱為RL串聯電路的時間常數。因此上面的公式又可表示為
\[I(t)=\dfrac{\mathscr{E}}{R}[1- e^{-\frac{t}{\tau}}\]
電流隨時間變化的關係可以用右圖來表示。這個曲線我們並不陌生，我們在討論電阻R-電容C-電池\(\mathscr{E}\)串聯的充電網路時，電容器上的電荷隨著時間的變化曲線也是這個函數：
\[Q(t)=C\mathscr{E}[1-e^{-\frac{t}{RC}}\]
當時間很大的時候，\(t \gg \tau\)，電流I接近於飽和值\(\dfrac{\mathscr{E}}{R}\)。\(t=\tau\)，此時電流到達其飽和值的0.63倍。我們也可以將電流微分在乘上電感值L，就可以得到感應線圈上反電動勢隨時間變化的函數：
\[\mathscr{E}_L=-L\dfrac{dI}{dt}=L(\dfrac{\mathscr{E}}{R})(1/\tau) e^{-\frac{t}{\tau}}=\mathscr{E} e^{-\frac{t}{\tau}}\]
\(t=0\)，\(\mathscr{E}_L=\mathscr{E}\)，隨著時間漸漸增加，感應反電動勢逐漸減小，在時間久遠之後(\(t >> \tau\))趨近0。也就是當電流趨近於飽和時，電流對時間不在變化，電感上的反電動勢就趨近於0。
例題：RL電路1:
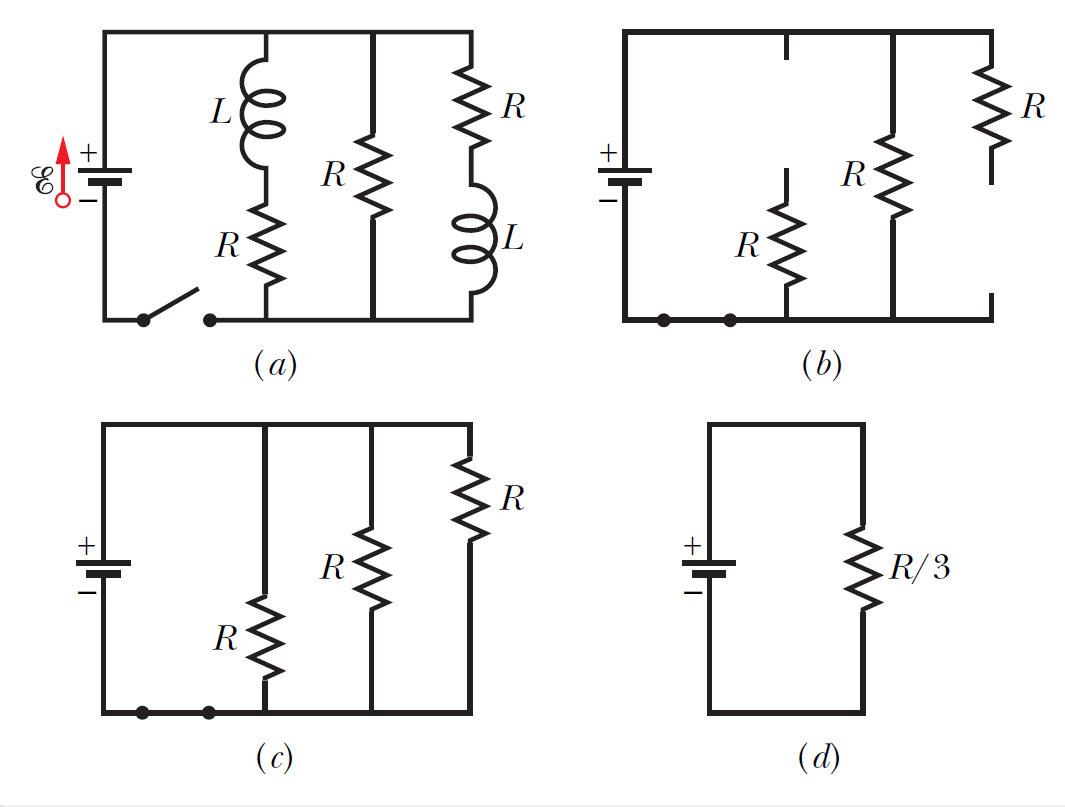右圖顯示了一個電路，其中包含三個相同的電阻，電阻為 \(R= 9.0 \, \Omega\)，兩個相同的電感為 \(L = 2.0\) mH，理想電池的電動勢為 \(\mathscr{E }=18\) V. (a) 在開關閉合後通過電池的電流 \(i\) 是多少？ (b) 開關閉合很長時間後通過電池的電流 \(i\) 是多少？
(a)
Because the current through each inductor is zero before the switch is closed, it will also be zero just afterward. Thus, immediately after the switch is closed, the inductors act as broken wires, as indicated in figure (b). We then have a single-loop circuit for which the loop rule gives us \[\mathscr{E}-iR=0; \quad i=\dfrac{\mathscr{E}}{R}=18/9=2\, \text{A}\] (b)
Long after the switch has been closed, the currents in the circuit have reached their equilibrium values, and the inductors act as simple connecting wires, as indicated in figure (c). We now have a circuit with three identical resistors in parallel; their equivalent resistance is \[R_{eq}=R/3=3 \,\Omega; \quad i=\dfrac{\mathscr{E}}{R_{eq}}=18/3=6\, \text{A}\]
例題：RL電路2:
例題：磁能:
我們在前面的討論中考慮了電流網路中可能的元件組合方式，包括電池-電阻-電容-開關，電池-電阻-電感-開關或者單純的有多個電池，電阻串聯並聯形成的複雜電阻網路。並且了解到電流網路中必須使用的兩個基本定理節點定理和迴路定理。在這些討論當中我們發現沒有電容和電感的網路，電流會維持定值，通過每一個電阻的電流都維持定值，不會隨時間改變其大小和流向，也就是所謂的直流電(DC, Direct Current)。在單純的RC和RL電路中，雖然通過電阻的電流會隨時間改變大小(大都是指數函數)，但是方向仍然固定。在這個小單元中，我們要介紹電阻-電容-電感結合成的RLC震盪網路，在這個網路當中通過電阻的電流不僅大小會隨時間改變，並且電流的流向也會隨時間改變，這種會正負交替的電流網路，我們稱交流(AC，Alternating Circuit)震盪網路。
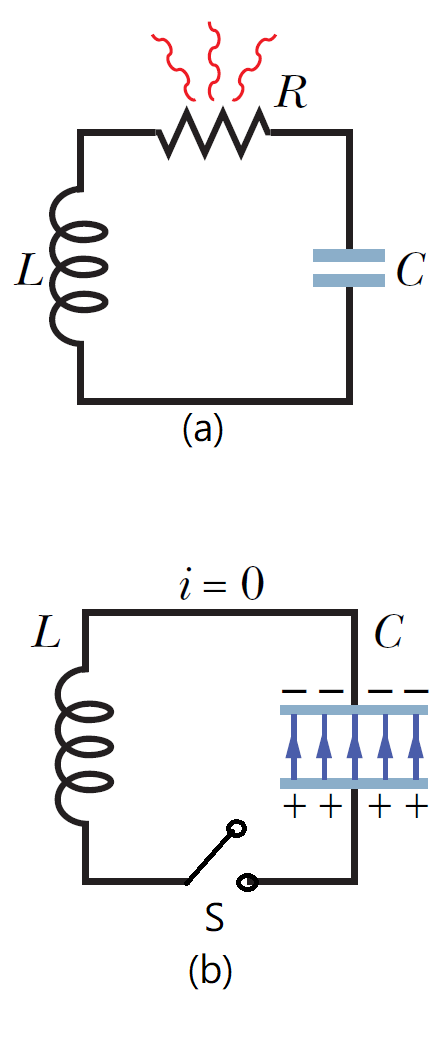
如右圖(a)所顯示的就是一個RLC震盪網路，我們先考慮右圖(b)只有LC的情況，也就是當電阻值非常小的時候，R可以忽略不計，而得到只有電感和電容形成的網路。在這個網路中如果一剛開始電容沒有電荷，電感也沒有電流，那麼什麼事情也不會發生，這樣的狀態會一直持續下去。但是如果初始狀態是電容保有一些電荷，並且開關S是打開的狀態，電路中沒有電流，電感沒有電流通過，正負電荷維持停留在電容的兩端，這是初始的狀態。假設在\(t=0\)的時候，我們將開關S連上，這時電路形成封閉迴路，電容上的電荷將開始流動。有電流通過電感，電感上會有磁通量通過，而磁通量隨時間的變化就會形成感應電動勢，因此這個封閉的迴路中，電位差要滿足迴路定理，其公式如下： \[Q/C-L\dfrac{dI}{dt}=0 \] 因為電流是電荷的微分，電容上的失去電荷量對時間的微分，\(I=-\dfrac{dQ}{dt}\)，因此我們將整個公式視為電荷的微分方程式，寫成如下的公式： \[L\dfrac{d^2}{dt^2}+CQ=0; \quad \dfrac{d^2}{dt^2}+\dfrac{1}{LC}Q=0\] 我們講上面公式整理之後不難發現，方程式的形式與簡諧震盪物體運動時的位置對時間的函數\(x(t)\)說要滿足的微分方程具有相同的形式： \[ \dfrac{d^2 x}{dt^2} + \dfrac{k}{m} x = 0 \] 我們已知簡諧震盪物體的位置對時間的函數是標準的三角函數，因此我們知道LC網路中的電荷\(Q(t)\)也會是一個時間的三角函數。換句話說電容上的電荷會發生振盪的行為，電容一端的正電荷會從最大的飽和值逐漸下降到0，又開始變成負電荷，負電荷的量持續增加直到負電荷的飽和值。電荷就這樣週期性的在正負飽和電荷之間振盪。我們可以直接寫下電荷對時間的函數如下： \[Q(t)=Q_0 \cos(\omega t + \phi), \quad \omega=\dfrac{1}{\sqrt{LC}}\] 同學們可以利用微分的運算，將下列的函數做兩次微分之後可以驗證這個函數滿足LC網路的微分方程式。為了滿足這個網路的初始條件\(t=0, \, Q(0)=Q_0, \, I(0)=0\)，我們選擇\(Q_0\)為飽和電荷值，相位角\(\phi=0\)。將電荷的時間函數微分可以得到通過電感的電流隨時間的函數關係： \[Q(t)=Q_0 \cos(\omega t)\] \[I(t)=-\dfrac{dQ}{dt}= \omega Q_0 \sin(\omega t)\] 這兩個物理量都是時間的三角函數，震盪的角頻率\(\omega=\dfrac{1}{\sqrt{LC}}\)，因此我們可以透過調整電容值C和電感值L得到不同的震盪頻率。從上面的討論我們可以明顯的看到電流的流向並非固定的，這種交替變換方向的電流稱為交流電。電力公司發電產生的電能就是透過交流電的方式，從發電廠將交流的電壓提升，再從發電廠傳送到城市中供我們日常使用。因為交流電可以透過螺線管不同圈數的互相感應，造成電壓的變化，也就是變壓器的基本原理，在同樣的距離中傳輸給定的發電功率，電位差越大電能傳輸中消耗的的焦耳熱就會越小。並且在我們用戶端可以利用交流電做各種不同的電壓改變，方便我們的應用。很多電器產品需要直流電，這時我們可以透過變壓、整流和濾波等基本原理，將交流電轉換成直流電，提供各種電器用品使用。
例題：LC circuit:
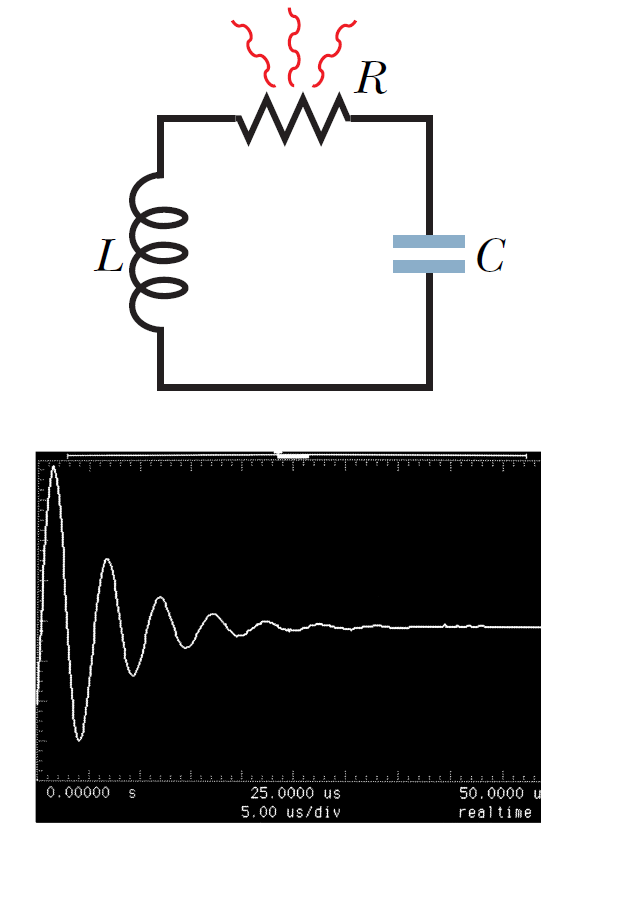最後我們考慮網路中除了有電容，電感之外還有電阻。這時網路的迴路定理必須加上電阻的電位差，公式如下：
\[Q/C-L\dfrac{dI}{dt}-RI=0\]
\[L\dfrac{d^2 Q}{dt^2} + R\dfrac{dQ}{dt} + \dfrac{1}{C}q=0 \]
這個微分方程的解答如下：
\[Q(t)=Q_0 e^{-\frac{Rt}{2L}} \cos(\omega' t + \phi) \]
\[\omega' = \sqrt{\omega^2 -(\frac{R}{2L}^2}; \quad \omega=\dfrac{1}{\sqrt{LC}}\]
比照上面的對應關係我們發現電阻所扮演的角色就是彈簧的簡諧震盪物體受到阻尼的影響，震盪的幅度會隨著時間越來越小，最後會停止震盪。如右圖所顯示，電容上的電荷震盪的幅度也會越來越小，最後所有的電荷都趨近於0，電流也近於0，所有的電能和磁能都轉換成為電阻的焦耳熱。
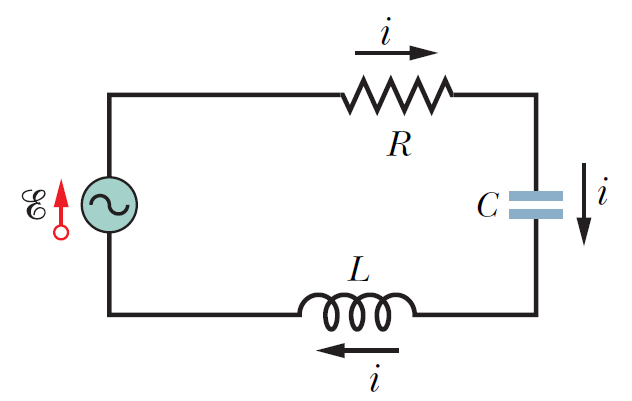同學們記得在簡諧震盪的討論中提到了共振的概念，就是震盪體系中遭受到外來的週期性力量的作用，如果外力的震盪頻率\(\omega_d\)非常接近震盪體系的自然頻率\(\omega_0\)時，簡諧震盪的振幅會持續的增加，也就是外界對震盪體系系統所做的功會源源不斷的增加系統的力學能，這個現象就叫做共振。在我們現在所討論的RLC網路中也有類似的情況，如果我們在RLC網路中加入一個交流電源\(\mathscr{E}=A \cos(\omega_d t)\)，這個交流電源的震盪幅度\(A\)可能不大，但是如果震盪頻率非常接近自然頻率\(\omega_d \simeq \omega_0=\dfrac{1}{\sqrt{LC}}\)也會發生共振現象。利用這個共振現象科學家在醫學檢測上發展出核磁共振攝影，其背後所使用的基本原理就有我們所探討的RLC共振現象。
授課教師
陳永忠 ycchen@thu.edu.tw
我們考慮一個細長的螺線管，半徑為\(a\)，長度為\(L\)，單位長度有\(n\)圈，那麼這個螺線管的自感可以計算如下：
當這個線圈上承載的穩定的電流\(I\)的時候，線圈內的均勻磁場其方向平行於線圈的長軸，\(B\)的大小為 \[B=\mu_0 n I\] 因此通過每一個線圈的磁通量 \[\Phi_B=B \pi a^2 =\mu_0 n I \pi a^2\] 通過\(N=nl\)圈的總磁通量為 \[N \Phi_B=B \pi a^2 =\mu_0 n I \pi a^2 N\] 因此它的自感可以表示為 \[L=\dfrac{N\Phi_B}{I}=\mu_0 n^2 \pi a^2 l\]
當這個線圈上承載的穩定的電流\(I\)的時候，線圈內的均勻磁場其方向平行於線圈的長軸，\(B\)的大小為 \[B=\mu_0 n I\] 因此通過每一個線圈的磁通量 \[\Phi_B=B \pi a^2 =\mu_0 n I \pi a^2\] 通過\(N=nl\)圈的總磁通量為 \[N \Phi_B=B \pi a^2 =\mu_0 n I \pi a^2 N\] 因此它的自感可以表示為 \[L=\dfrac{N\Phi_B}{I}=\mu_0 n^2 \pi a^2 l\]
RL電路
考慮一個自感為\(L\)的線圈與一個電阻值為\(R\)的電阻，以及一個電動勢為\(\mathscr{E}\)的直流電池構成的電路，如右圖所示。假設電池的內電阻以及感應線圈的電阻都遠小於\(R\)，可忽略不計。並且假設開關\(S\)按下前，電路上的電流為0。當開關\(S\)在\(t=0\)按下時，電路接通，電流開始增加。同時在感應線圈上出現一個感應電動勢\(\mathscr{E}_L\)對抗電池的電動勢，因為\(\mathscr{E}_L\)對抗\(\mathscr{E}\)，所以又稱為反電動勢。根據電感的定義我們有下列的關係
\[\mathscr{E}_L=-L\dfrac{dI}{dt}\]
利用迴路定理我們可以得到下面關於電位差的公式：
\[\mathscr{E}-IR-L\dfrac{dI}{dt}=0\]
上面的公式稍加整理可以得到如下關於電流\(I\)的微分方程式
\[\dfrac{dI}{dt}+\dfrac{R}{L}I=\dfrac{\mathscr{E}}{L}\]
同樣的，我們不在這邊講解如何求解這個微分方程式，而直接把這個為微分方程式的解直接列出如下的電流函數
\[I(t)=\dfrac{\mathscr{E}}{R}-I_0 e^{-\frac{Rt}{L}}\]
我們知道初始條件\(t=0\)，\(I=0\)，所以我們得到上面公式的\(I_0=\dfrac{\mathscr{E}}{R}\)。因此上面的公式又可以寫成
\[I(t)=\dfrac{\mathscr{E}}{R}[1- e^{-\frac{t}{L/R}}\]
其中指數函數的常數\(\tau=L/R\)稱為RL串聯電路的時間常數。因此上面的公式又可表示為
\[I(t)=\dfrac{\mathscr{E}}{R}[1- e^{-\frac{t}{\tau}}\]
電流隨時間變化的關係可以用右圖來表示。這個曲線我們並不陌生，我們在討論電阻R-電容C-電池\(\mathscr{E}\)串聯的充電網路時，電容器上的電荷隨著時間的變化曲線也是這個函數：
\[Q(t)=C\mathscr{E}[1-e^{-\frac{t}{RC}}\]
當時間很大的時候，\(t \gg \tau\)，電流I接近於飽和值\(\dfrac{\mathscr{E}}{R}\)。\(t=\tau\)，此時電流到達其飽和值的0.63倍。我們也可以將電流微分在乘上電感值L，就可以得到感應線圈上反電動勢隨時間變化的函數：
\[\mathscr{E}_L=-L\dfrac{dI}{dt}=L(\dfrac{\mathscr{E}}{R})(1/\tau) e^{-\frac{t}{\tau}}=\mathscr{E} e^{-\frac{t}{\tau}}\]
\(t=0\)，\(\mathscr{E}_L=\mathscr{E}\)，隨著時間漸漸增加，感應反電動勢逐漸減小，在時間久遠之後(\(t >> \tau\))趨近0。也就是當電流趨近於飽和時，電流對時間不在變化，電感上的反電動勢就趨近於0。例題：RL電路1:
右圖顯示了一個電路，其中包含三個相同的電阻，電阻為 \(R= 9.0 \, \Omega\)，兩個相同的電感為 \(L = 2.0\) mH，理想電池的電動勢為 \(\mathscr{E }=18\) V. (a) 在開關閉合後通過電池的電流 \(i\) 是多少？ (b) 開關閉合很長時間後通過電池的電流 \(i\) 是多少？(a)
Because the current through each inductor is zero before the switch is closed, it will also be zero just afterward. Thus, immediately after the switch is closed, the inductors act as broken wires, as indicated in figure (b). We then have a single-loop circuit for which the loop rule gives us \[\mathscr{E}-iR=0; \quad i=\dfrac{\mathscr{E}}{R}=18/9=2\, \text{A}\] (b)
Long after the switch has been closed, the currents in the circuit have reached their equilibrium values, and the inductors act as simple connecting wires, as indicated in figure (c). We now have a circuit with three identical resistors in parallel; their equivalent resistance is \[R_{eq}=R/3=3 \,\Omega; \quad i=\dfrac{\mathscr{E}}{R_{eq}}=18/3=6\, \text{A}\]
例題：RL電路2:
A solenoid has an inductance of 53 mH and a resistance of 0.37 . If the solenoid is connected to a battery, how long will the current take to reach half its final equilibrium value?
The current as a function of time is given as \[i(t)=\dfrac{\mathscr{E}}{R} \left( 1-e^{-t/\tau_L} \right) \] \[\dfrac{\mathscr{E}}{2R} \left( 1-e^{-t_0/\tau_L} \right) \Rightarrow t_0=\tau_L \ln 2=\dfrac{L}{R} \ln 2=\dfrac{53 \times 10^{-3}}{0.37} \ln 2= 0.10 \, \text{s}\]
The current as a function of time is given as \[i(t)=\dfrac{\mathscr{E}}{R} \left( 1-e^{-t/\tau_L} \right) \] \[\dfrac{\mathscr{E}}{2R} \left( 1-e^{-t_0/\tau_L} \right) \Rightarrow t_0=\tau_L \ln 2=\dfrac{L}{R} \ln 2=\dfrac{53 \times 10^{-3}}{0.37} \ln 2= 0.10 \, \text{s}\]
磁場能量
一個載有電流的線圈擁有能量，並且因為電流產生磁場，所以電流的能量稱為磁場能量，也稱為磁能。一個電荷系統的電能定義為，在電荷系統建立過程中，外力對抗電荷間的庫侖力所必須做的功。電流的磁能也採取類似的定義方法。這個問題我們可以利用\(\mathscr{E}-R-L\)的迴路定理的公式得到答案。迴路定理的電位差公式如下： \[\mathscr{E}=IR + L\dfrac{dI}{dt}\] 把公式的兩邊都乘上電流\(I\)， \[\mathscr{E}I=I^2R + LI\dfrac{dI}{dt}\] \(\mathscr{E}I\)是電池在單位時間內所提供的能量，\(I^2R\)是電阻\(R\)在單位時間內所消耗的焦耳熱，因此從能量守恆考量，\(LI\dfrac{dI}{dt}\)代表線圈的磁能在單位時間內的增加速率。如果以\(U_B\)表示總體磁能，那麼磁能對時間的微分，\(dU_B/dt\)，就是磁能的功率。當\(t=0\)，\(I=0\)，\(U_B=0\)，我們可以將上面的公式對時間積分，得到當線圈承載的電流為\(I\)時，電感儲存的磁能為 \[U_B=\dfrac{1}{2} L I^2\] 對於電荷系統我們在討論電能的時候，定義了電能密度(單位體積內的電能)，我們發現電能密度是與電場的平方成正比。同樣的，對於磁能的討論中，我們也可以定義單位體積內的磁能，也就是磁能密度，我們發現磁能密度與磁場的強度平方成正比。關於這一點我們可以利用理想的螺線管來找到這個關係。考慮上面例體中的螺線管，半徑為\(a\)，長度為\(l\)，單位長度有n圈的螺線管。這個螺線管的自感為 \[L=\mu_0 n^2 \pi a^2 l\] 當這個螺旋管承載電流\(I\)時，線圈內的磁場值為\(B=\mu_0 n I\)，所儲存的磁能根據上面的公式為 \[ U_B=1/2(\mu_0 n^2 \pi a^2 l) I^2=\dfrac{1}{2\mu_0}(\mu_0 n I)^2 (\pi a^2 l)\] \[U_B=(\dfrac{B^2}{2 \mu_0})(\pi a^2 l)\] 上式中，\(\pi a^2 l\)為螺旋管所包圍的體積，所求的磁能密度為 \[u_B=\dfrac{B^2}{2 \mu_0} \] 所以我們得到非常有趣的結果：電場和磁場的能量對應公式有非常緊密的對稱性。整理上面所有的公式，我們不難發現電感也可以用磁能來定義其公式如下 \[U_B=\int \dfrac{B^2}{2\mu_0} \, dV\] \[L=\dfrac{2U_B}{I^2}=\dfrac{2}{I^2} \int \dfrac{B^2}{2 \mu_0}\, dV\]例題：磁能:
A coil has an inductance of 53 mH and a resistance of 0.35 . (a) If a 12 V emf is applied across the coil, how much energy is stored in the magnetic field after the current has built up to its equilibrium value? (b) After how many time constants will half this equilibrium energy be stored in the magnetic field?
The energy stored in the magnetic field of a coil at any time depends on the current through the coil at that time, according to \(U_B(t)=1/2 L i^2(t)\).
\[i(t)=\dfrac{\mathscr{E}}{R} \left( 1-e^{-t/\tau_L} \right) \] \[i_{\infty}=\dfrac{\mathscr{E}}{R}=12/0.35=34.3 \, \text{V}\] \[U_B(\infty)=1/2 L i_{\infty}^2=31 \,\text{J}\] (a)
The current as a function of time is given as \[i(t)=\dfrac{\mathscr{E}}{R} \left( 1-e^{-t/\tau_L} \right) \] \[\dfrac{\mathscr{E}}{2R} \left( 1-e^{-t_0/\tau_L} \right) \Rightarrow t_0=\tau_L \ln 2=\dfrac{L}{R} \ln 2=\dfrac{53 \times 10^{-3}}{0.37} \ln 2= 0.10 \, \text{s}\] (b)
\[U_B(t_0)=1/2U_B(\infty)\] \[1/2 L i^2=(1/2)(1/2)L i_{\infty}^2\] \[e^{-t/\tau_L}=1-\dfrac{1}{\sqrt{2}}=0.293\] \[t \simeq 1.23 \tau_L\]
The energy stored in the magnetic field of a coil at any time depends on the current through the coil at that time, according to \(U_B(t)=1/2 L i^2(t)\).
\[i(t)=\dfrac{\mathscr{E}}{R} \left( 1-e^{-t/\tau_L} \right) \] \[i_{\infty}=\dfrac{\mathscr{E}}{R}=12/0.35=34.3 \, \text{V}\] \[U_B(\infty)=1/2 L i_{\infty}^2=31 \,\text{J}\] (a)
The current as a function of time is given as \[i(t)=\dfrac{\mathscr{E}}{R} \left( 1-e^{-t/\tau_L} \right) \] \[\dfrac{\mathscr{E}}{2R} \left( 1-e^{-t_0/\tau_L} \right) \Rightarrow t_0=\tau_L \ln 2=\dfrac{L}{R} \ln 2=\dfrac{53 \times 10^{-3}}{0.37} \ln 2= 0.10 \, \text{s}\] (b)
\[U_B(t_0)=1/2U_B(\infty)\] \[1/2 L i^2=(1/2)(1/2)L i_{\infty}^2\] \[e^{-t/\tau_L}=1-\dfrac{1}{\sqrt{2}}=0.293\] \[t \simeq 1.23 \tau_L\]
LC振盪網路
我們在前面的討論中考慮了電流網路中可能的元件組合方式，包括電池-電阻-電容-開關，電池-電阻-電感-開關或者單純的有多個電池，電阻串聯並聯形成的複雜電阻網路。並且了解到電流網路中必須使用的兩個基本定理節點定理和迴路定理。在這些討論當中我們發現沒有電容和電感的網路，電流會維持定值，通過每一個電阻的電流都維持定值，不會隨時間改變其大小和流向，也就是所謂的直流電(DC, Direct Current)。在單純的RC和RL電路中，雖然通過電阻的電流會隨時間改變大小(大都是指數函數)，但是方向仍然固定。在這個小單元中，我們要介紹電阻-電容-電感結合成的RLC震盪網路，在這個網路當中通過電阻的電流不僅大小會隨時間改變，並且電流的流向也會隨時間改變，這種會正負交替的電流網路，我們稱交流(AC，Alternating Circuit)震盪網路。如右圖(a)所顯示的就是一個RLC震盪網路，我們先考慮右圖(b)只有LC的情況，也就是當電阻值非常小的時候，R可以忽略不計，而得到只有電感和電容形成的網路。在這個網路中如果一剛開始電容沒有電荷，電感也沒有電流，那麼什麼事情也不會發生，這樣的狀態會一直持續下去。但是如果初始狀態是電容保有一些電荷，並且開關S是打開的狀態，電路中沒有電流，電感沒有電流通過，正負電荷維持停留在電容的兩端，這是初始的狀態。假設在\(t=0\)的時候，我們將開關S連上，這時電路形成封閉迴路，電容上的電荷將開始流動。有電流通過電感，電感上會有磁通量通過，而磁通量隨時間的變化就會形成感應電動勢，因此這個封閉的迴路中，電位差要滿足迴路定理，其公式如下： \[Q/C-L\dfrac{dI}{dt}=0 \] 因為電流是電荷的微分，電容上的失去電荷量對時間的微分，\(I=-\dfrac{dQ}{dt}\)，因此我們將整個公式視為電荷的微分方程式，寫成如下的公式： \[L\dfrac{d^2}{dt^2}+CQ=0; \quad \dfrac{d^2}{dt^2}+\dfrac{1}{LC}Q=0\] 我們講上面公式整理之後不難發現，方程式的形式與簡諧震盪物體運動時的位置對時間的函數\(x(t)\)說要滿足的微分方程具有相同的形式： \[ \dfrac{d^2 x}{dt^2} + \dfrac{k}{m} x = 0 \] 我們已知簡諧震盪物體的位置對時間的函數是標準的三角函數，因此我們知道LC網路中的電荷\(Q(t)\)也會是一個時間的三角函數。換句話說電容上的電荷會發生振盪的行為，電容一端的正電荷會從最大的飽和值逐漸下降到0，又開始變成負電荷，負電荷的量持續增加直到負電荷的飽和值。電荷就這樣週期性的在正負飽和電荷之間振盪。我們可以直接寫下電荷對時間的函數如下： \[Q(t)=Q_0 \cos(\omega t + \phi), \quad \omega=\dfrac{1}{\sqrt{LC}}\] 同學們可以利用微分的運算，將下列的函數做兩次微分之後可以驗證這個函數滿足LC網路的微分方程式。為了滿足這個網路的初始條件\(t=0, \, Q(0)=Q_0, \, I(0)=0\)，我們選擇\(Q_0\)為飽和電荷值，相位角\(\phi=0\)。將電荷的時間函數微分可以得到通過電感的電流隨時間的函數關係： \[Q(t)=Q_0 \cos(\omega t)\] \[I(t)=-\dfrac{dQ}{dt}= \omega Q_0 \sin(\omega t)\] 這兩個物理量都是時間的三角函數，震盪的角頻率\(\omega=\dfrac{1}{\sqrt{LC}}\)，因此我們可以透過調整電容值C和電感值L得到不同的震盪頻率。從上面的討論我們可以明顯的看到電流的流向並非固定的，這種交替變換方向的電流稱為交流電。電力公司發電產生的電能就是透過交流電的方式，從發電廠將交流的電壓提升，再從發電廠傳送到城市中供我們日常使用。因為交流電可以透過螺線管不同圈數的互相感應，造成電壓的變化，也就是變壓器的基本原理，在同樣的距離中傳輸給定的發電功率，電位差越大電能傳輸中消耗的的焦耳熱就會越小。並且在我們用戶端可以利用交流電做各種不同的電壓改變，方便我們的應用。很多電器產品需要直流電，這時我們可以透過變壓、整流和濾波等基本原理，將交流電轉換成直流電，提供各種電器用品使用。
例題：LC circuit:
A \(1.5 \, \mu F\) capacitor is charged to 57 V. The charging battery is then disconnected, and a 12 mH coil is connected in series with the capacitor so that LC oscillations occur. What is the maximum current in the coil? Assume that the circuit contains no resistance, which would cause the energy to be dissipated.
\[U_{E,max}=U_{B,max}; \quad \dfrac{Q^2}{2C}=\dfrac{LI^2}{2}\] \[I=\sqrt{\dfrac{Q^2}{LC}}=\sqrt{\dfrac{(CV)^2}{LC}}=V\sqrt{\dfrac{C}{L}}=0.637 \, \text{A}. \]
\[U_{E,max}=U_{B,max}; \quad \dfrac{Q^2}{2C}=\dfrac{LI^2}{2}\] \[I=\sqrt{\dfrac{Q^2}{LC}}=\sqrt{\dfrac{(CV)^2}{LC}}=V\sqrt{\dfrac{C}{L}}=0.637 \, \text{A}. \]
RLC振盪網路
最後我們考慮網路中除了有電容，電感之外還有電阻。這時網路的迴路定理必須加上電阻的電位差，公式如下：
\[Q/C-L\dfrac{dI}{dt}-RI=0\]
\[L\dfrac{d^2 Q}{dt^2} + R\dfrac{dQ}{dt} + \dfrac{1}{C}q=0 \]
這個微分方程的解答如下：
\[Q(t)=Q_0 e^{-\frac{Rt}{2L}} \cos(\omega' t + \phi) \]
\[\omega' = \sqrt{\omega^2 -(\frac{R}{2L}^2}; \quad \omega=\dfrac{1}{\sqrt{LC}}\]
比照上面的對應關係我們發現電阻所扮演的角色就是彈簧的簡諧震盪物體受到阻尼的影響，震盪的幅度會隨著時間越來越小，最後會停止震盪。如右圖所顯示，電容上的電荷震盪的幅度也會越來越小，最後所有的電荷都趨近於0，電流也近於0，所有的電能和磁能都轉換成為電阻的焦耳熱。
同學們記得在簡諧震盪的討論中提到了共振的概念，就是震盪體系中遭受到外來的週期性力量的作用，如果外力的震盪頻率\(\omega_d\)非常接近震盪體系的自然頻率\(\omega_0\)時，簡諧震盪的振幅會持續的增加，也就是外界對震盪體系系統所做的功會源源不斷的增加系統的力學能，這個現象就叫做共振。在我們現在所討論的RLC網路中也有類似的情況，如果我們在RLC網路中加入一個交流電源\(\mathscr{E}=A \cos(\omega_d t)\)，這個交流電源的震盪幅度\(A\)可能不大，但是如果震盪頻率非常接近自然頻率\(\omega_d \simeq \omega_0=\dfrac{1}{\sqrt{LC}}\)也會發生共振現象。利用這個共振現象科學家在醫學檢測上發展出核磁共振攝影，其背後所使用的基本原理就有我們所探討的RLC共振現象。
授課教師
陳永忠 ycchen@thu.edu.tw