幾何光學
根據馬克斯威爾的電磁學理論光波是一種電磁波,因此光學可說是電磁學的一部分,一般常將能引發人眼視覺的電磁波稱呼為可見光或簡稱為光。光的波長遠小於開口或障礙物的尺寸時,其行進的路線可視為直線,稱為光線(beam)和射線(ray)。在點光源照射下形成的影子,其幾何形狀與開口或阻擋物的輪廓相似,這就是光線直進的例子。根據光線的概念,可利用幾何學的方法探討光的現象,例如反射與折射現象,這種光學是我們這一個單元的主要內容,稱呼為線光學或幾何光學。這個單元將會說明光的反射與折射現象所必須遵循的基本定律,並介紹一些相關的現象例如色散、全反射等。另外我們也將介紹基本的幾何光學重要的反射面和透鏡成像的基本原理,並且也會介紹基本的光學儀器,例如照相機、望遠鏡和顯微鏡。波長與物體開口或障礙物的尺寸接近時,光的波動性質較為明顯,會出現波動特有的繞射轉彎與干涉等現象。這些無法以直進的光線來說明的現像是我們下一個單元的重點,這樣的光學特性我們稱呼為物理光學或波動光學。
介質
光波可以在真空中或透明的介質中傳播,所謂介質可以是真空或透明物質。光在一個介質中傳播時如遇到另一種介質,通常有一部分會被反射回到原來的介質中,其餘的部分則會透射而進入另一介質。這與力學波的反射與透射的現象是相同的。金屬的表面通常能將入射光大部分的能量反射,這是因為金屬表面的自由電子在入射光的電磁場作用下會震動,而出現加速度因而發出電磁波,將光的能量傳回原來的介質中,這也使金屬表面顯得光亮。有些物質在被光照射時,會將入射光大部分的能量吸收,因此反射和透射的光相當微弱,看起來暗黑且不透明。而另外一些介質光可以透射通過,幾乎不會有任何能量被吸收,因此看起來是透明的,這類介質通常是電的絕緣體,如空氣、玻璃、石英、壓克力。電磁波在介質中行進的速度會變慢,利用介質中行進的速度與真空中的速度做比較我們可以定一折射率:\(n=\dfrac{c}{v}\),介質的材料不同造成折射率大小不同。反射
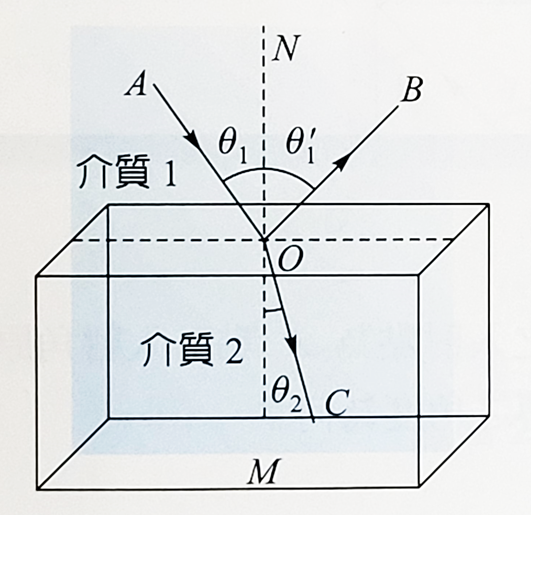 兩介質的相鄰接觸面稱為介面,當光由介質1傳播到介質2時,
在介面處其前進的方向改變,入射的光線稱為入射線。如圖中所示,\(AO\)是入射線,\(OB\)是反射線,\(AC\)是折射線。入射線、反射線和折射線與介面的交點稱為入射點。通過入射點且與介面垂直的直線稱為法線(\(N\)),入射線與法線的夾角稱為入射角\(\theta_1\),反射線與法線的夾角稱為反射角\(\theta_1'\),折射線與法線的夾角稱為折射角\(\theta_2\)。入射線與法線所在的平面稱為入射面。當發生反射的時候,入射光的能量會有一部分甚至全部返回到原來的介質中,根據實驗結果,光在反射時須遵守反射定律,
兩介質的相鄰接觸面稱為介面,當光由介質1傳播到介質2時,
在介面處其前進的方向改變,入射的光線稱為入射線。如圖中所示,\(AO\)是入射線,\(OB\)是反射線,\(AC\)是折射線。入射線、反射線和折射線與介面的交點稱為入射點。通過入射點且與介面垂直的直線稱為法線(\(N\)),入射線與法線的夾角稱為入射角\(\theta_1\),反射線與法線的夾角稱為反射角\(\theta_1'\),折射線與法線的夾角稱為折射角\(\theta_2\)。入射線與法線所在的平面稱為入射面。當發生反射的時候,入射光的能量會有一部分甚至全部返回到原來的介質中,根據實驗結果,光在反射時須遵守反射定律,- 入射線、反射線和法線均在入射面上,且相交於入射點。
- 入射線與反射線位於法線的兩側,且入射角等於反射角。 \[\theta_1 = \theta_1 '\]
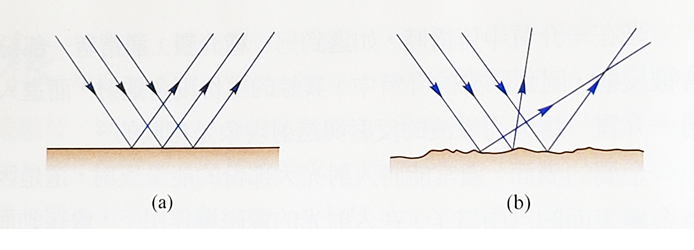 根據反射定律,當一束光平行射入光滑平面時,每一光線的反射角都相同,因此反射後的光束,各光束的方向仍舊是平行而一致的,這種反射稱為鏡面反射。在粗造不平的表面上產生的反射,每一光線的入射角仍然等於反射角,但反射線的方向散亂不一致,這個現象稱為漫反射或簡稱為漫射(如左圖)。
根據反射定律,當一束光平行射入光滑平面時,每一光線的反射角都相同,因此反射後的光束,各光束的方向仍舊是平行而一致的,這種反射稱為鏡面反射。在粗造不平的表面上產生的反射,每一光線的入射角仍然等於反射角,但反射線的方向散亂不一致,這個現象稱為漫反射或簡稱為漫射(如左圖)。折射現象
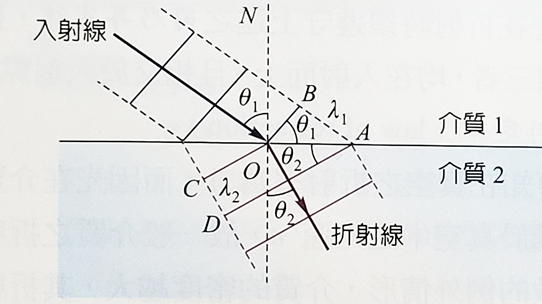 當光到達二透明介質的介面時,有一部分的光線被反射回到原來的介質中,而其餘部分的光則透射進入另一介質。透射的光其前進的方向與入射方向不同,這個現象稱為折射現象。
當光到達二透明介質的介面時,有一部分的光線被反射回到原來的介質中,而其餘部分的光則透射進入另一介質。透射的光其前進的方向與入射方向不同,這個現象稱為折射現象。折射現象發生的原因是光在介面兩邊的透明介質具有不同的波速,如右圖所示,由於在任何一段時間內經由介質1抵達介面上OA部分的入射波,與透射通過此部分介面進入介質2中傳播的波,其數目相同,故折射後的波在介質2中,每單位時間內傳播波的數目,亦即折射波的頻率(f)與週期(T)均與入射波相同。由於兩介質的波速不同,入射波的波長\(\lambda_1\)與折射波的波長\(\lambda_2\)不同,假設在介質1,介質2中的波速分別為\(v_1, \, v_2\),光波之入射角與折射角分別為\(\theta_1, \, \theta_2\)。右圖顯示入射波與折射波,其中與行進方向垂直的線段代表波的波峰位置,相鄰兩波峰之時間間隔為1週期,相鄰兩波峰之距離為一個波長: \[AB=OA \sin \theta_1 = \lambda_1; \quad CD=OA \sin \theta_2= \lambda_2\] \[OA=\dfrac{\lambda_1}{\sin \theta_1}=\dfrac{\lambda_2}{\sin \theta_2}\] 因為波長的公式 \[\lambda_1 = v_1 T; \quad \lambda_2 = v_2 T\] 上面的公式可以寫成 \[\dfrac{v_1}{\sin \theta_1}=\dfrac{v_2}{\sin \theta_2} \] 如果將光在真空中的速度\(c\)與在一介質中的速度\(v\)的比值,定義為該介質的折射率(index of refraction): \[n=\dfrac{c}{v}; \quad n_1=\dfrac{c}{v_1}; \quad n_2=\dfrac{c}{v_2} \] 上面的比例關係可以透過介質的折射率\(n_1, \, n_2\)改寫成 \[ n_1 \sin \theta_1 = n_2 \sin \theta_2 \] \[ n_1 \lambda_1= n_2 \lambda_2 \] 這個式子稱為笛卡爾定律或者叫做Snell定律。
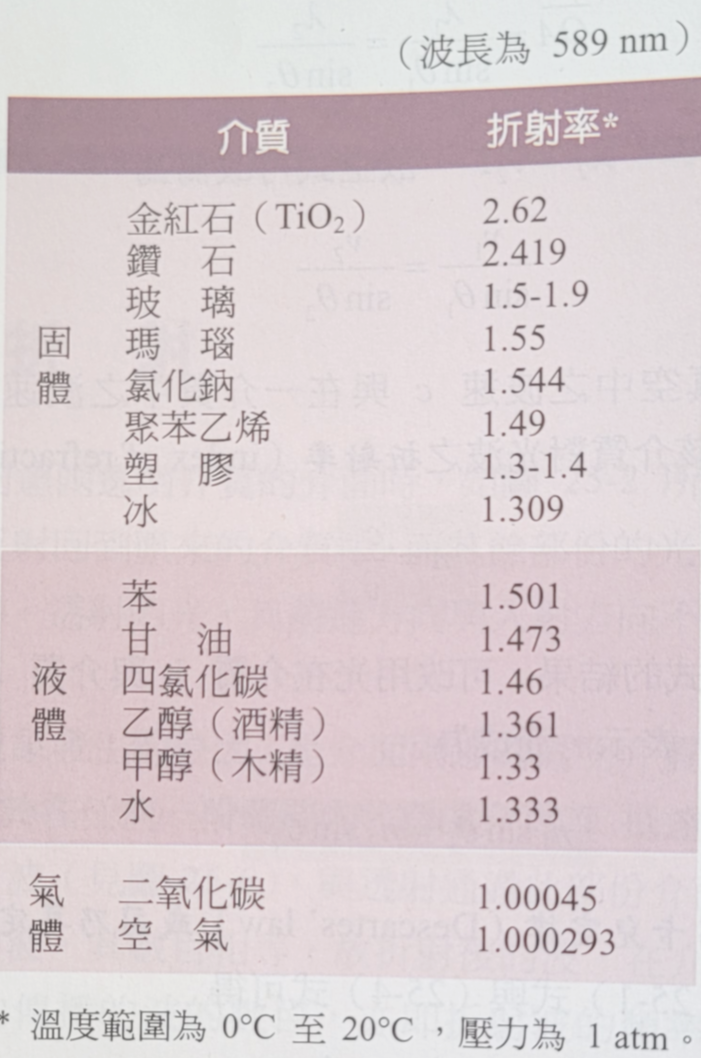 根據實驗結果光在折射時須遵守上面的Snell定律,入射線、折射線與法線三者均在入射面上,並且相交於入射點,這一個結果就統稱為光的折射定律。已知真空的折射率是1,因光在介質中的波速一般都低於真空中的波速,所以一般介質之折射率都大於1。除了少數的例外情形,介質的密度越大折射率也越高。一般而言,氣體的折射率與其密度成正比,空氣的折射率相當接近1。不少的礦物具有相當高的折射率,如琉砷銀礦的折射率約為3.1,在右側的表中我們列出一些透明介質對光的折射率。
根據實驗結果光在折射時須遵守上面的Snell定律,入射線、折射線與法線三者均在入射面上,並且相交於入射點,這一個結果就統稱為光的折射定律。已知真空的折射率是1,因光在介質中的波速一般都低於真空中的波速,所以一般介質之折射率都大於1。除了少數的例外情形,介質的密度越大折射率也越高。一般而言,氣體的折射率與其密度成正比,空氣的折射率相當接近1。不少的礦物具有相當高的折射率,如琉砷銀礦的折射率約為3.1,在右側的表中我們列出一些透明介質對光的折射率。當光由折射率較小的介質進入折射率較大的介質時,根據折射定律折射角將小於入射角,也就是折射線會比入射線更貼近法線;反之當光由折射率較大的介質,進入折射率較小的介質時,折射線會比入射線更偏離法線。兩個介質中折射率較大者稱為光密介質,而折射率較小者稱為光疏介質。
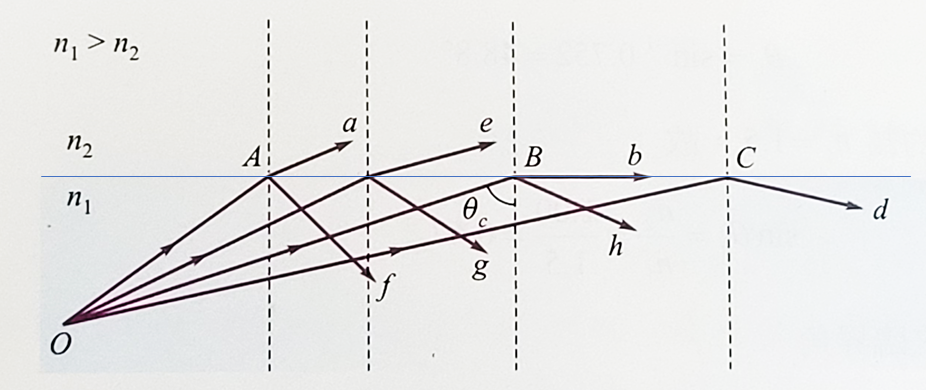 根據折射定律:當光由空氣進入水中時,也就是光入射到光密介質,折射角會小於入射角,且入射角越小折射角也越小,在此情況下折射線會比入射線更靠近法線。反過頭來,如果光由水進入空氣時,光入射到光疏介質,折射線會比入射線更偏離法線。如果入射角持續增大,則折射角也隨之變大。直到折射線的折射角達到最大值90度的時候,折射線將與界面平行,此時入射角稱為臨界角(critical angle)。根據折射定律,臨界角的定義公式可表示如下
\[n_1 \sin \theta_1 = n_2 \sin \theta_2, \quad n_1 \sin \theta_c = n_2 \sin(90^{\circ}) \Rightarrow \sin \theta_c = \dfrac{n_2}{n_1} \]
如果入射角沒有超過臨界角,那麼會同時觀察到折射光和反射光;如果入射角大於臨界角,折射光不會折射進入光疏介質中,而會完全反射回光密介質中,這種沒有折射現象伴隨發生的反射稱為全反射(total internal reflection)。全反射現象的應用很廣,主要是因發生全反射時,所有入射至介面的光全部被反射回原來的介質中,因此反射光的強度不會減弱。相對的,一般的鏡面反射,即使反射面非常光滑,反射光也一定比入射光弱,因此雙筒望遠鏡、潛望鏡、相機等通常都採用全反射稜鏡,而非鏡面反射面鏡,以反射光線。
根據折射定律:當光由空氣進入水中時,也就是光入射到光密介質,折射角會小於入射角,且入射角越小折射角也越小,在此情況下折射線會比入射線更靠近法線。反過頭來,如果光由水進入空氣時,光入射到光疏介質,折射線會比入射線更偏離法線。如果入射角持續增大,則折射角也隨之變大。直到折射線的折射角達到最大值90度的時候,折射線將與界面平行,此時入射角稱為臨界角(critical angle)。根據折射定律,臨界角的定義公式可表示如下
\[n_1 \sin \theta_1 = n_2 \sin \theta_2, \quad n_1 \sin \theta_c = n_2 \sin(90^{\circ}) \Rightarrow \sin \theta_c = \dfrac{n_2}{n_1} \]
如果入射角沒有超過臨界角,那麼會同時觀察到折射光和反射光;如果入射角大於臨界角,折射光不會折射進入光疏介質中,而會完全反射回光密介質中,這種沒有折射現象伴隨發生的反射稱為全反射(total internal reflection)。全反射現象的應用很廣,主要是因發生全反射時,所有入射至介面的光全部被反射回原來的介質中,因此反射光的強度不會減弱。相對的,一般的鏡面反射,即使反射面非常光滑,反射光也一定比入射光弱,因此雙筒望遠鏡、潛望鏡、相機等通常都採用全反射稜鏡,而非鏡面反射面鏡,以反射光線。
 折射與全反射是光纖的基礎,常見的光纖管的管芯為細絲,直徑約8微米(\(\mu\)m),一般使用透明的光疏介質如玻璃或塑膠,包覆管心的是一層或多層的光疏介質,越靠外表的折射率越低。光纖通常使用波長為0.851,1.31和1.55微米的紅外光,當光進入光纖管後會在介面發生全反射,或者因多層光疏介質折射可以在近乎沒有衰減的情況下沿著光纖管前進。
折射與全反射是光纖的基礎,常見的光纖管的管芯為細絲,直徑約8微米(\(\mu\)m),一般使用透明的光疏介質如玻璃或塑膠,包覆管心的是一層或多層的光疏介質,越靠外表的折射率越低。光纖通常使用波長為0.851,1.31和1.55微米的紅外光,當光進入光纖管後會在介面發生全反射,或者因多層光疏介質折射可以在近乎沒有衰減的情況下沿著光纖管前進。物體發出的光線在經光纖管的管壁多次全反射和折射後,方向以經失真,故單一的光纖或光導管無法用來傳遞物體的真實影像。為了解決這個問題,就是將許多的光纖絲集合成為光纖束(optical fiber bundle)。每一條纖絲只傳送給小部分的物體影像。醫學上觀察胃、腸、膀胱、支氣管時使用的各種光纖內視鏡都依此原理製成。光導管也可用來提供照明,以便進行內科醫學手術。
在現代的光纖通訊系統中,光可以近乎不衰減的沿著光纖傳播到數公里外,而若在傳送途中,已雷射增強其訊號,則可用以從事跨越洲際的遠距離通訊。利用光纖從事通訊,除了訊號不易失真與管線更耐用之外,其成本也低廉許多,這是因為光的頻率甚高,其頻寬遠高於傳統通訊使用的微波。一條玻璃光纖可以同時載送的電話高達數萬通,而一條銅線只能再送數十通。
例題
Calculate the speed of light in zircon, a material used in jewelry to imitate diamond. \(n_{zircon}=1.923\)
計算鋯石中的光速,鋯石是一種用於珠寶模仿鑽石的材料。
\(v=\dfrac{c}{n}=\dfrac{3 \times 10^8}{1.923}=1.56 \times 10^8 \text{m/s}\)
計算鋯石中的光速,鋯石是一種用於珠寶模仿鑽石的材料。
\(v=\dfrac{c}{n}=\dfrac{3 \times 10^8}{1.923}=1.56 \times 10^8 \text{m/s}\)
例題
Find the index of refraction for medium 2. Assuming medium 1 is air and given the incident angle is \(30^{\circ}\) and the angle of refraction is \(22^{\circ}\).
求介質 2 的折射率。假設介質 1 是空氣,入射角為 \(30^{\circ}\),折射角為 \(22^{\circ}\)。
\(n_1 \sin \theta_1 = n_2 \sin \theta_2; \quad 1 \cdot \sin(30^{\circ}) = n_2 \sin (22^{\circ}) \Rightarrow n_2=1.33\)
求介質 2 的折射率。假設介質 1 是空氣,入射角為 \(30^{\circ}\),折射角為 \(22^{\circ}\)。
\(n_1 \sin \theta_1 = n_2 \sin \theta_2; \quad 1 \cdot \sin(30^{\circ}) = n_2 \sin (22^{\circ}) \Rightarrow n_2=1.33\)
例題
What is the critical angle for light traveling in a polystyrene (a type of plastic, \(n=1.49\)) pipe surrounded by air?
光在被空氣包圍的聚苯乙烯(一種塑料,\(n=1.49\))管中傳播的臨界角是多少? \[\theta_c = \sin^{-1} \dfrac{n_1}{n_2}=\sin^{-1} \dfrac{1}{1.49}=\sin^{-1} (0.671)=42.2^{\circ}\]
光在被空氣包圍的聚苯乙烯(一種塑料,\(n=1.49\))管中傳播的臨界角是多少? \[\theta_c = \sin^{-1} \dfrac{n_1}{n_2}=\sin^{-1} \dfrac{1}{1.49}=\sin^{-1} (0.671)=42.2^{\circ}\]
例題
(a)請計算光由水進入空氣之臨界角。(b)請計算光由玻璃進入空氣之臨界角。(c)請計算光由玻璃進入水之臨界角。
(a)\[\theta_c = \sin^{-1} \dfrac{n_1}{n_2}=\sin^{-1} \dfrac{1}{1.33}=\sin^{-1} (0.75)=48.6^{\circ}\] (b)\[\theta_c = \sin^{-1} \dfrac{n_1}{n_2}=\sin^{-1} \dfrac{1}{1.5}=\sin^{-1} (0.667)=41.8^{\circ}\] (c)\[\theta_c = \sin^{-1} \dfrac{n_1}{n_2}=\sin^{-1} \dfrac{1.33}{1.5}=\sin^{-1} (0.887)=62.5^{\circ}\]
一道光線由空氣進入玻璃中時,其行進方向偏折5度,則此光線的入射角是多少度? Answer:14.8。
(a)\[\theta_c = \sin^{-1} \dfrac{n_1}{n_2}=\sin^{-1} \dfrac{1}{1.33}=\sin^{-1} (0.75)=48.6^{\circ}\] (b)\[\theta_c = \sin^{-1} \dfrac{n_1}{n_2}=\sin^{-1} \dfrac{1}{1.5}=\sin^{-1} (0.667)=41.8^{\circ}\] (c)\[\theta_c = \sin^{-1} \dfrac{n_1}{n_2}=\sin^{-1} \dfrac{1.33}{1.5}=\sin^{-1} (0.887)=62.5^{\circ}\]
一道光線由空氣進入玻璃中時,其行進方向偏折5度,則此光線的入射角是多少度? Answer:14.8。
色散
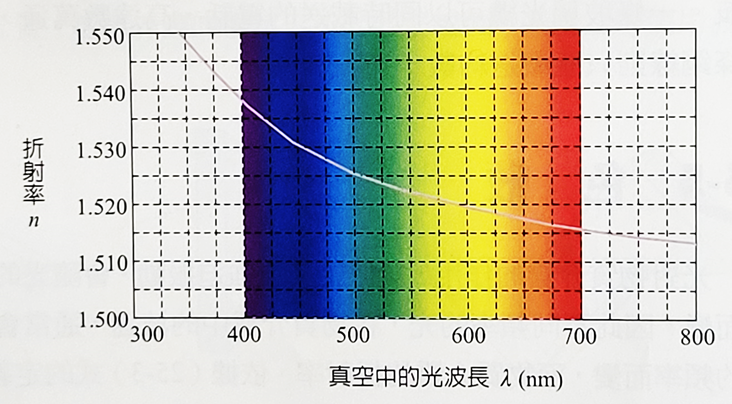 光對介質的物質作用類似於一種強迫震動(forced oscillation),介質分子振動的幅度會隨光的頻率而改變。因此不同顏色的光以不同的頻率與介質分子作用之後,在物質介質中的波速會隨光的頻率而變,速度的改變就造成不同顏色的光發生不同角度的折射。而根據折射率的定義,不同的折射角意味著不同的顏色(頻率)的光,在同一個介質中會有不同的折射率。所以結論就是,物質介質的折射率會隨頻率而改變,但是在真空中各種頻率的光和電磁波其波速均相同,所以折射率都是1。當一道由多種顏色和波長的光線合成的平行光束例如太陽光,斜射至介質的界面時,光的折射率隨顏色而變,各色的光線在折射後因折射角彼此不同,就會分散開來,沿不同的方向前進,此一現象稱為色散(dispersion)。在右圖當中我們顯示了光學儀器常用的玻璃,對各種不同波長的折射率的變化圖,波長較長的光折射率較小。牛頓在1666年時,發現白色的陽光在通過玻璃三稜鏡後,會產生偏向,並色散成7種色光,依紅、橙、黃、綠、藍、靛、紫的偏向順序,形成光譜(spectrum)。其中紅光的偏向最小,紫光最大。他同時也發現各種色光可以合成為白光。
光對介質的物質作用類似於一種強迫震動(forced oscillation),介質分子振動的幅度會隨光的頻率而改變。因此不同顏色的光以不同的頻率與介質分子作用之後,在物質介質中的波速會隨光的頻率而變,速度的改變就造成不同顏色的光發生不同角度的折射。而根據折射率的定義,不同的折射角意味著不同的顏色(頻率)的光,在同一個介質中會有不同的折射率。所以結論就是,物質介質的折射率會隨頻率而改變,但是在真空中各種頻率的光和電磁波其波速均相同,所以折射率都是1。當一道由多種顏色和波長的光線合成的平行光束例如太陽光,斜射至介質的界面時,光的折射率隨顏色而變,各色的光線在折射後因折射角彼此不同,就會分散開來,沿不同的方向前進,此一現象稱為色散(dispersion)。在右圖當中我們顯示了光學儀器常用的玻璃,對各種不同波長的折射率的變化圖,波長較長的光折射率較小。牛頓在1666年時,發現白色的陽光在通過玻璃三稜鏡後,會產生偏向,並色散成7種色光,依紅、橙、黃、綠、藍、靛、紫的偏向順序,形成光譜(spectrum)。其中紅光的偏向最小,紫光最大。他同時也發現各種色光可以合成為白光。
分光計
 將一個三稜鏡擺在平面圓的中心,使一些已知波長的光,沿圓的半徑入射至三稜鏡,再將這些光的出射方向,分別標示於圓週上當作波長的參考尺標。然後我們將一個待測的入射光源照射三稜鏡後,會在圓週上出現不同的色光,因此利用製備好的波長尺標,確定這個待測光源當中有哪些波長的光組成。這種裝置稱為稜鏡分光計(prism spectrometer)。液體和固體發出的光其光譜的波長分布是連續的,而氣體發出的則是不連續,具有特定波長的光譜線。利用能產生色散的裝置,如稜鏡分光計可由光譜的波長分佈情形辨識出光源含有何種元素,此種方法稱為光譜分析學或光譜學(spectroscopy)。光譜學在科學研究上非常有用,例如在地質學中,可用來辨識礦石,而在天文學中用以測定遙遠星球上各種元素含量的多寡。在光學儀器中,色散的現象通常只有徒增困擾。例如不同顏色的光通過玻璃透鏡的鏡頭後,由於折射率不同會有不同的焦點,因此形成的像會出現一種畸變,稱為色像差(chromatic abberation),必須使用不同折射率的玻璃透鏡所組成的複合鏡頭,才能夠消除這個變形。
將一個三稜鏡擺在平面圓的中心,使一些已知波長的光,沿圓的半徑入射至三稜鏡,再將這些光的出射方向,分別標示於圓週上當作波長的參考尺標。然後我們將一個待測的入射光源照射三稜鏡後,會在圓週上出現不同的色光,因此利用製備好的波長尺標,確定這個待測光源當中有哪些波長的光組成。這種裝置稱為稜鏡分光計(prism spectrometer)。液體和固體發出的光其光譜的波長分布是連續的,而氣體發出的則是不連續,具有特定波長的光譜線。利用能產生色散的裝置,如稜鏡分光計可由光譜的波長分佈情形辨識出光源含有何種元素,此種方法稱為光譜分析學或光譜學(spectroscopy)。光譜學在科學研究上非常有用,例如在地質學中,可用來辨識礦石,而在天文學中用以測定遙遠星球上各種元素含量的多寡。在光學儀器中,色散的現象通常只有徒增困擾。例如不同顏色的光通過玻璃透鏡的鏡頭後,由於折射率不同會有不同的焦點,因此形成的像會出現一種畸變,稱為色像差(chromatic abberation),必須使用不同折射率的玻璃透鏡所組成的複合鏡頭,才能夠消除這個變形。
光學系統
光學系統如面鏡顯微鏡望遠鏡照相機眼鏡眼睛等能夠藉由反射和折射改變光的行進方向嬰兒可使入射的光形成一種視覺圖樣而能將食物或景物的形體顯現出來稱為相下面我們將進行幾何學幾何光學的進式來探討一些常見光學系統的成像原理與特性 透過成像系統看一個物體時到達眼睛的光雖然看來都像是從物體發出沿著直線直接傳來但這些光的行進路線其實已被成像系統改變過因此人眼看到的相就位置大小和方位而言與實際物體並不一定相同當進入人眼的光確實是像從其所在之位置發出時稱此項為10相若實際並非由相之遺志發出兒子是看是如此時則稱為虛像若於相的位置放一瓶沐則10項可將屏幕照亮虛像則對屏幕毫無作用Two Types of Image
比如說,為了讓你看到一隻企鵝,你的眼睛必須攔截一些從企鵝發出的光線,然後將它們重定向到眼睛後部的視網膜上。你的視覺系統,從視網膜開始,到大腦後部的視覺皮層結束,會自動和下意識地處理光提供的信息。該系統識別邊緣、方向、紋理、形狀和顏色,然後迅速將企鵝的圖像(源自光的複製品)帶入您的意識; 你感知並認出企鵝是在光線來自的方向和適當的距離。例如,如果光線從標準平面鏡向您反射,企鵝似乎在鏡子後面,因為您攔截的光線來自那個方向。 當然,企鵝不在後面。這種被稱為虛像的圖像,真正只存在於大腦中,但據說存在於感知的位置。 實像的不同之處在於它可以在表面上形成,例如卡片或電影屏幕。您可以看到真實的圖像(否則電影院將是空的),但是圖像的存在並不取決於您是否看到它,即使您沒有看到它也存在。
平面鏡
整理儀容常用平面的反射鏡稱為平面鏡鏡前的人可以看到自己在鏡中的像比較像與真人則可發現兩者與鏡面等距離均為正力大小並無不同但左右相反一般物體可視為由多點組成且對應於每一誤點的像點集合起來就成為物體的像可可得到以下的結論平面鏡所成之相恆為虛像各務點到其對應點的連線與鏡面垂直個點之相距等於物距所以像與物體的大小與形狀相同並且為正立上面的結論中物體和相相對於平面鏡所具有的幾何關係稱為面鏡對稱如將左手掌放置於平面鏡前方那麼所成的像看起來會像右手掌因此相像的左手掌和右手掌就是一面就是一種面鏡對稱的關係曲面鏡
反射面為曲面的鏡子稱為曲面鏡,平面鏡能形成大小不變的正立虛像,曲面鏡所成的像大小可以改變,正立和到立都有可能,而除了虛像之外也可以是實像。拋物面鏡
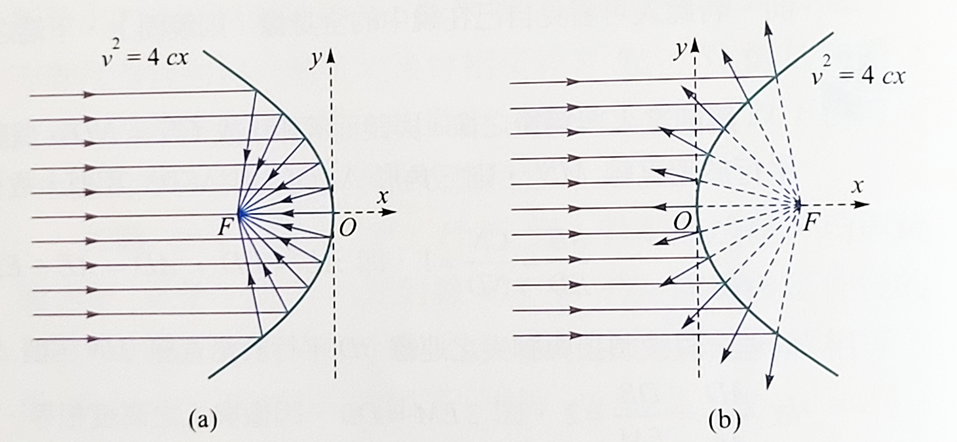 如圖所示,拋物線以其頂點為平面直角坐標系的原點,則以拋物線的對稱軸為x軸時,拋物線的方程式可表示為:\(y^2=4cx\)。焦點\(F=(c,0)\),焦距=|c|。這個拋物線繞x軸旋轉半週所形成的迴轉面,稱為拋物迴轉麵,簡稱為拋物面。反射面為拋物面的鏡子,稱為拋物迴轉面鏡,簡稱拋物面鏡。拋物面鏡有一個特性,就是所有平行於對稱軸的入射光線,其反射線或反射線向鏡後延伸時,必然通過同一個點,這個點稱呼為焦點。所以拋物面鏡常用於反射式天文望遠鏡,以使遠方星球成像於焦點時,能較為明亮。反之,將光源置於拋物面鏡的焦點,則經鏡面反射後的光線都平行於鏡軸,所以照明燈具,如探照燈,手電筒和汽機車的頭燈,常利用這種方式提供平行光束,使光得以投射到遠處。
如圖所示,拋物線以其頂點為平面直角坐標系的原點,則以拋物線的對稱軸為x軸時,拋物線的方程式可表示為:\(y^2=4cx\)。焦點\(F=(c,0)\),焦距=|c|。這個拋物線繞x軸旋轉半週所形成的迴轉面,稱為拋物迴轉麵,簡稱為拋物面。反射面為拋物面的鏡子,稱為拋物迴轉面鏡,簡稱拋物面鏡。拋物面鏡有一個特性,就是所有平行於對稱軸的入射光線,其反射線或反射線向鏡後延伸時,必然通過同一個點,這個點稱呼為焦點。所以拋物面鏡常用於反射式天文望遠鏡,以使遠方星球成像於焦點時,能較為明亮。反之,將光源置於拋物面鏡的焦點,則經鏡面反射後的光線都平行於鏡軸,所以照明燈具,如探照燈,手電筒和汽機車的頭燈,常利用這種方式提供平行光束,使光得以投射到遠處。球面鏡
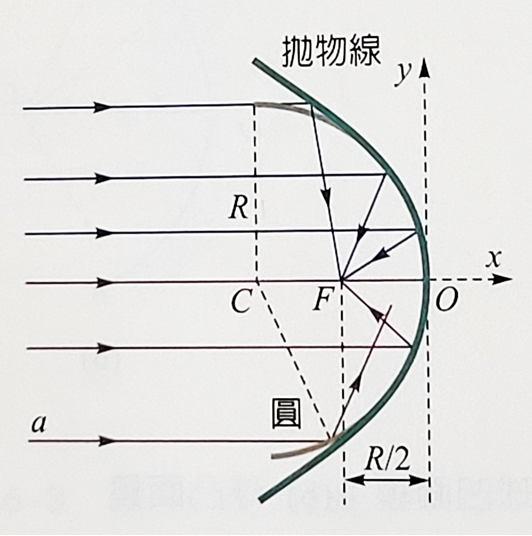 圓心位於\((R,0)\),半徑為\(R\)的圓,可表示為\(y^2 + (x-R)^2=R^2\)。對近軸光線而言,因為只入射到球面鏡位於近頂點附近的部分(\(|x| \ll R\)),所以上面的方程式可以改寫為
\[0=y^2 + x^2 + x(x-2R) \simeq y^2 - 2Rx \\ y^2 \simeq 2Rx=4fx; \quad f=R/2.\]
其中\(f=c\)是拋物線的焦距。這個結果顯示,圓可近視為焦距\(f\)等於\(R/2\)的拋物線(\(f=\dfrac{R}{2}\)),焦點就位在\((\dfrac{R}{2}, 0)\)的位置。換言之,對近軸光線而言,球凹面鏡就如同拋物凹面鏡一樣,可將平行於主軸的光線匯聚到鏡頂\(O\)與曲率中心\(C\)的中點\(F\),\(f=R/2\)。
圓心位於\((R,0)\),半徑為\(R\)的圓,可表示為\(y^2 + (x-R)^2=R^2\)。對近軸光線而言,因為只入射到球面鏡位於近頂點附近的部分(\(|x| \ll R\)),所以上面的方程式可以改寫為
\[0=y^2 + x^2 + x(x-2R) \simeq y^2 - 2Rx \\ y^2 \simeq 2Rx=4fx; \quad f=R/2.\]
其中\(f=c\)是拋物線的焦距。這個結果顯示,圓可近視為焦距\(f\)等於\(R/2\)的拋物線(\(f=\dfrac{R}{2}\)),焦點就位在\((\dfrac{R}{2}, 0)\)的位置。換言之,對近軸光線而言,球凹面鏡就如同拋物凹面鏡一樣,可將平行於主軸的光線匯聚到鏡頂\(O\)與曲率中心\(C\)的中點\(F\),\(f=R/2\)。球面鏡由於反射面較為規則,比拋物面鏡更易製作,所以一般聚焦多選用球面鏡,例如哈伯太空望遠鏡。但大面積的球面鏡無法像拋物面鏡一樣,將所有與主軸平行的光線匯聚到單一的焦點,這種缺失稱為球面像差(spherical aberration)。如果只使用一小部分的球面作為鏡面,則可降低這種像差。
根據光的反射定律,畫出多條入射線與反射線,可求得平面鏡或曲面鏡所成的像,這個方法稱為光線描跡法或稱為作圖法。一個物點經過物鏡反射所成的像點,通常都有通常都可以用兩條反射光線實際或延伸後的交點決定。若球面鏡可近似為拋物面,那麼在計算球面成像時,可以用下面的方式作圖:
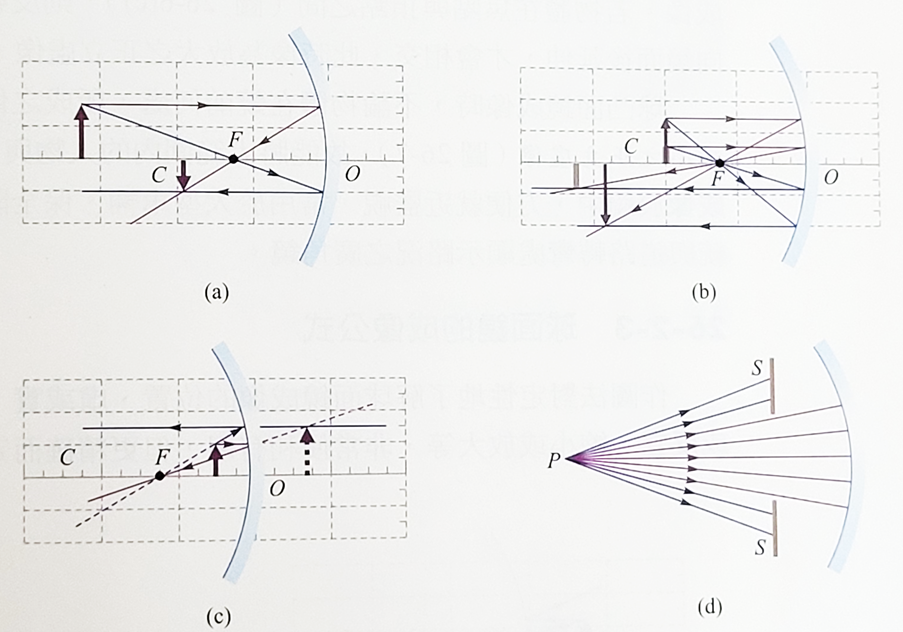
- 入射線平行於主軸時反射線與其延伸線必通過交點。
- 入射線或其延伸線通過焦點\(F\)時,反射線必平行於主軸。
- 入射線通過曲率中心\(C\)時,反射線與入射線反向,且兩者都與鏡面垂直。
- 通過頂點\(O\)的入射線與反射線,與主軸之夾角相等。
如果鏡面的尺度尺寸遠小於球面鏡且物點位於主軸附近,與鏡面有些距離,則所有入射線與反射線都為近軸光線,像差微小可忽略,圖中帶有箭頭的垂線就是物體的像。所以只考慮近軸光線的時候,球面鏡的成像問題會變得比較簡單。如圖所示的阻隔物\(S\)稱為孔徑光闌(aperture stop),可限制鏡面範圍使通過的光線成為近軸光線已減少像差的光線。在我們下面的討論中,除非我們有特別說明,否則所有成像的光線都假設為近軸光線。
凹面鏡成像的時候若物體在區域中心C之外,則成為縮小的倒立實像,如湯匙的凹面所成的像;如果物體放在曲率中心與焦點之間,則會成為放大倒立實像,且像比物體更遠離鏡面。物體越接近焦點,實像越大,離鏡面也越遠。若物體位在焦點上,那麼反射線全部平行於主軸,無法相交成像。若物體在焦點與頂點之間,則反射線均向鏡面後方延伸才會相交,此時像為放大之正立虛像。
球凸面鏡成像時,不論物體在鏡前何處,所成之相恆為縮小之正立虛像,所以能將大範圍內的人物與景象,成像於鏡中,方便就近監視,常用於大型車輛、保全防盜系統與道路轉彎處顯示路況之廣角鏡。
球面鏡的成像公式
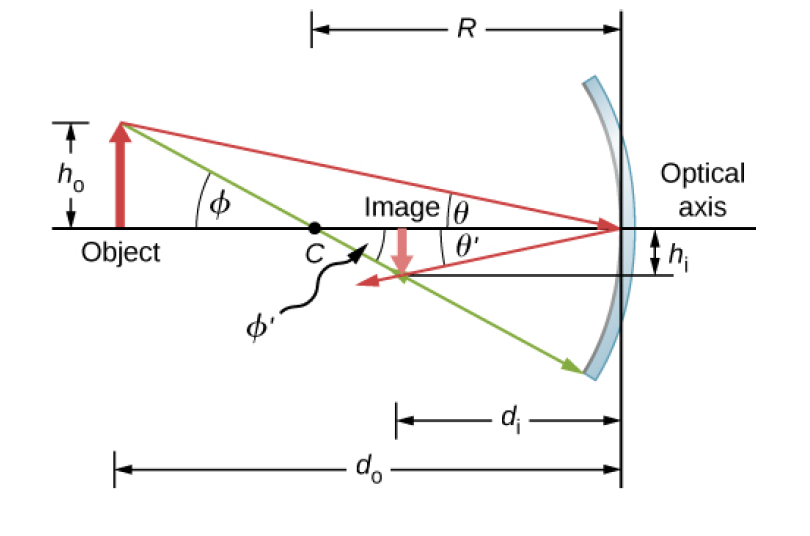
在這個小節中我們先列出球面鏡的成像公式,以及這些公式的應用,至於這些公式的推導,我們會另外一個頁面來說明。以右圖為例,球面鏡的焦點以\(F\)表示,球面鏡的曲率中心以\(C\)表示,物體放置的位置以\(P\)點表示,經曲面鏡反射後成像的位置以\(P'\)點表示。為了能夠清楚應用下面的公式於面鏡的計算,我們首先說明距離的符號定義,這個符號規定稱呼為笛卡兒符號制。- 球面鏡的頂點\(O\)選擇為座標的原點,沿著鏡軸向右為正x軸方向,沿著主軸向上為正y方向。
- 假設真實物體放在球面鏡的左側,光線最初由左向右入入射至曲面鏡。(物距\(s \lt 0\))
- 在曲面鏡成像的作圖當中,位置和向量都以座標形式表示,所以位置和向量相對於座標的原點和座標軸,可能是正也可能是負。\(AB=BA\)代表對兩個點,不同的指向,會得到正負不同的向量。例如圖中的各點位置座標可表示為: \[A=(l,0), \, B=(l,h), \, C=(l,-H)\] 圖中的各個位移量依據x軸與y軸的方向都帶有正負符號,圖中的各位移量可表示為: \[OA=l, \quad AO=-l, \quad AB=h, \quad AC=-H。\]
- 逆時針方向的夾角為正,順時針方向的夾角為負。 \[\angle{AOB} \gt 0; \quad \angle{AOC} \lt 0; \quad \angle{ABO} \lt 0; \quad \angle{OAB}=-90^{\circ}\] \(\angle{AOB}\)指的是向量OA繞O點旋轉到向量OB時,絕對值不超過180度的角。
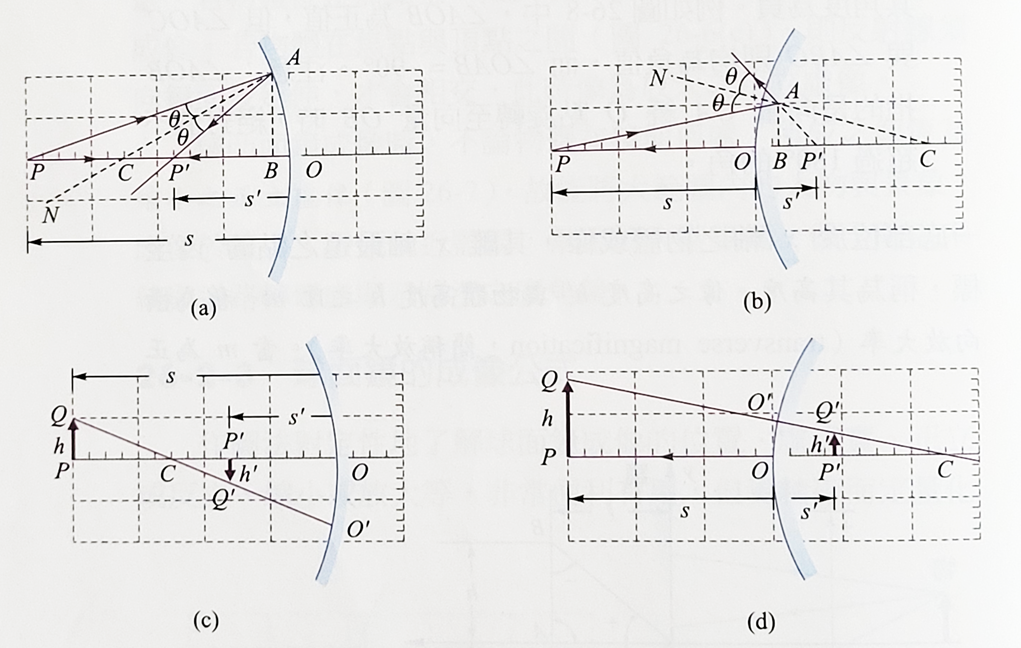
上圖中我們看到求啊面鏡和求凸面鏡的成像作圖。 頂點\(O\)到\(F\)的距離\(OF\)就是球面鏡的焦距\(f\),球面鏡的焦距是球面半徑的一半, \[f=\dfrac{R}{2} \quad 凹面鏡的焦距是負的,凸面鏡的焦距是正的。\] 物體放置地點是\(P\)點,假設寫成\(s\),我們叫做物距,像點以\(P'\)表示,距離\(OP'=s'\)像距。 由光的反射定律我們可以寫下這些這三個距離\(f,s,s'\)之間必須滿足的關係如下: \[\dfrac{1}{s}+\dfrac{1}{s'}=\dfrac{1}{f}=\dfrac{2}{R}.\] 如圖所顯示的,物體的高度\(h\)與像的高度\(h'\)不一定相同,這兩者之間的比例就是放大率\(m\): \[m=-\dfrac{s'}{s}\]
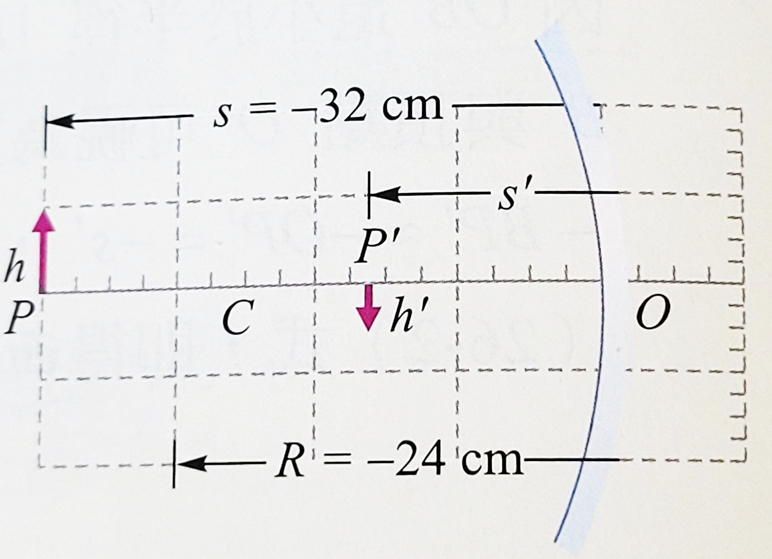 我們以凹面鏡的一個例子,來說明上面公式的應用。如右圖所示一個高度為2.0 cm的物體,直立於半徑為24 cm的球凹面鏡前方32 cm處,請計算(a)凹面鏡的焦距,(b)像距,(c)放大率,(d)像的高度,(e)像是直立或倒立,(f)是實像或虛像。
我們以凹面鏡的一個例子,來說明上面公式的應用。如右圖所示一個高度為2.0 cm的物體,直立於半徑為24 cm的球凹面鏡前方32 cm處,請計算(a)凹面鏡的焦距,(b)像距,(c)放大率,(d)像的高度,(e)像是直立或倒立,(f)是實像或虛像。(a)\( f=-\dfrac{R}{2}=-\dfrac{24}{2}=-12 \,\text{cm}\)
(b)\(f=-12; \,\, s=-32; \quad \\ \dfrac{1}{s'}=\dfrac{1}{f}-\dfrac{1}{s}=\dfrac{1}{-12}-\dfrac{1}{-32}=-\dfrac{5}{96}; \quad s'=-19.2 \,\text{cm}\)
表示像位於鏡的左方,也就是曲面鏡的前方。
(c)放大率\(m=-\dfrac{s'}{s}=-\dfrac{-19.2}{-32}=-0.6\)
(d)像的高度\(h'=h \times m=2(-0.6)=-1.2 \,\text{cm}\)
(e)像的高度為負值所以是倒立。
(f)像位於面鏡的前方所以是實像。
 |
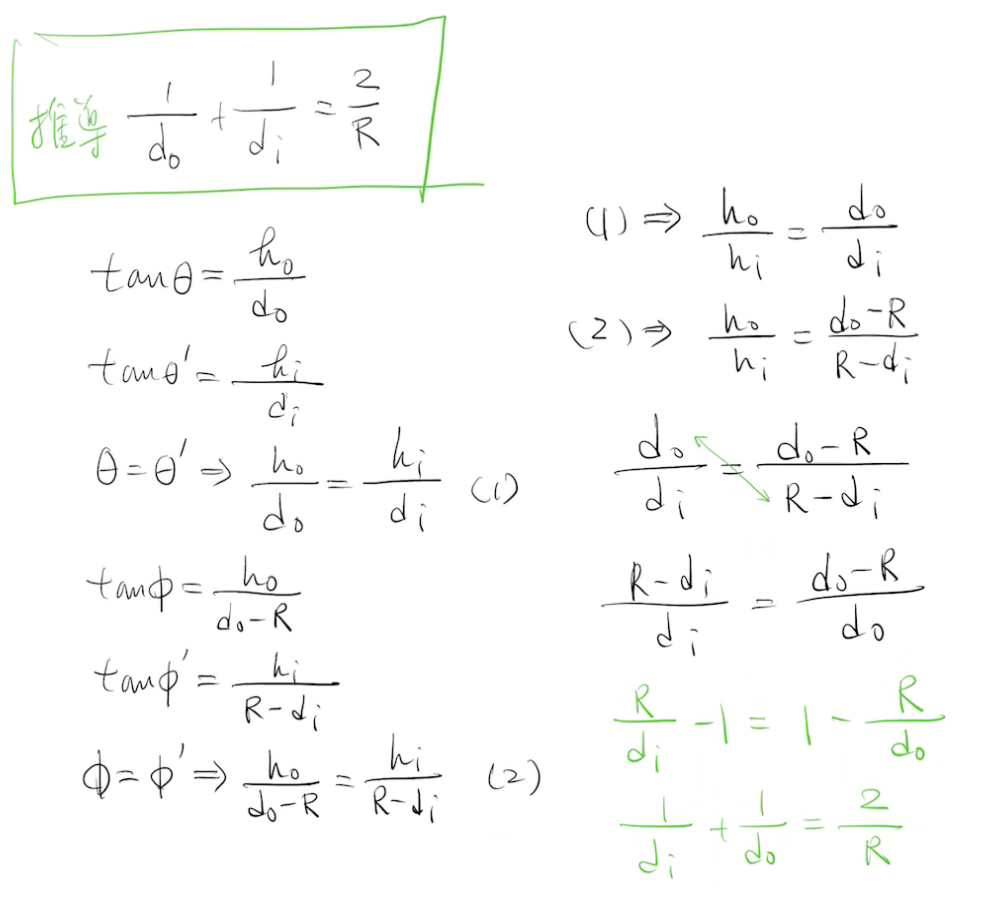 |
球面透鏡
球面的折射
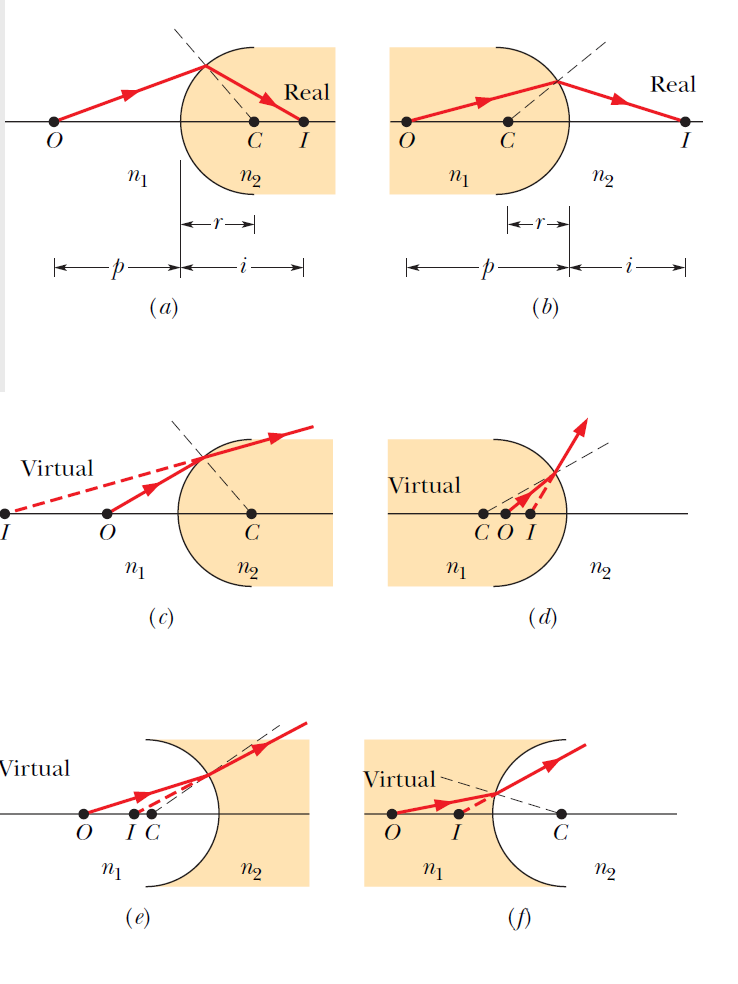 我們現在從反射形成的圖像轉向通過透明材料(例如玻璃)的表面折射形成的圖像。我們只考慮球面,曲率半徑為\(r\),曲率中心為\(C\)。光將由在折射率為 \(n_1\)的介質中的點物體自\(O\)點發射;它將通過球面折射到折射率為\(n_2\)的介質中。我們關心的是光線在通過表面折射後是形成實像(不需要觀察者)還是虛像(假設觀察者截取光線)。答案取決於\(n_1\)和\(n_2\)的相對值以及幾何形狀。右圖顯示了六種可能的結果。 在圖中的每一部分,具有較大折射率的介質被塗上陰影,物體\(O\)總是在折射率為\(n_1\)的介質中,在折射面的左側。在每個圖中,顯示了一條有代表性的(紅色)光線通過表面折射。
我們現在從反射形成的圖像轉向通過透明材料(例如玻璃)的表面折射形成的圖像。我們只考慮球面,曲率半徑為\(r\),曲率中心為\(C\)。光將由在折射率為 \(n_1\)的介質中的點物體自\(O\)點發射;它將通過球面折射到折射率為\(n_2\)的介質中。我們關心的是光線在通過表面折射後是形成實像(不需要觀察者)還是虛像(假設觀察者截取光線)。答案取決於\(n_1\)和\(n_2\)的相對值以及幾何形狀。右圖顯示了六種可能的結果。 在圖中的每一部分,具有較大折射率的介質被塗上陰影,物體\(O\)總是在折射率為\(n_1\)的介質中,在折射面的左側。在每個圖中,顯示了一條有代表性的(紅色)光線通過表面折射。在每條光線的折射點,折射面的法線是通過曲率中心\(C\)的徑向線。由於折射,如果光線進入折射率較大的介質,行進方向將會靠近法線,如果它進入折射率較小的介質則偏離法線。如果彎曲將光線發送到中心軸,則該光線和其他光線(未繪製)在該軸上形成真實圖像。 如果經過折射之後光線的行進彎向中央光軸,那麼將會形成實像;如果折射後的光線遠離中央軸,將會形成虛像。因為點物體還有另外一個行進的光線,就是沿著光軸傳遞的光線,因此紅色的光線與光軸的交點就是成像的位置。折射光線的向後延伸,會形成一個虛像,前提是(就像鏡子一樣)其中一些光線被觀察者截獲。實像 I 在圖 34-12 的 a 和 b 部分形成(在像距離 i 處),其中折射將光線引向中心軸。虛像在 c 和 d 部分形成,其中折射引導光線遠離中心軸。注意,在這四個部分中,當物體離折射面較遠時形成實像,當物體靠近折射面時形成虛像。在最終情況下(圖 34-12e 和 f),無論物距如何,折射總是將光線引導離開中心軸,並且總是形成虛像。
薄透鏡的成像公式
透鏡是具有兩個中心軸重合的折射面的透明物體。共同的中心軸是鏡片的中心軸。當鏡片被空氣包圍時,光線從空氣折射進入鏡片,穿過鏡片,然後折射回到空氣中。 每次折射都可以改變光的行進方向。 使最初平行於中心軸的光線會聚的透鏡(合理地)稱為會聚透鏡。 相反,如果它使這些光線發散,則該透鏡是發散透鏡。 當一個物體放置在任一類型的鏡頭前時,來自該物體的光線折射進出該鏡頭可以產生該物體的圖像。由於折射定律我們知道當光線通過透鏡的時候,也會改變光的行進方向,相對於曲面鏡光的行進樂滿足反射定律,在透鏡成像的時候要使用折射定律。同樣的,我們不會在這個網頁中推導透鏡成像的公式,我們只把透鏡成像所要依循的公式列出來,並且帶著同學做幾個例題,以便能夠了解如何應用透鏡成像的原理,來了解如何設計光學儀器。
實像形成在與物體相對的折射表面的一側,而虛像形成在與物體相同的一側。
在球面鏡的成像當中,我們首先要決定面鏡的焦距,對球面鏡非常簡單,球面鏡的焦距就是曲率半徑的一半。對於薄透鏡而言,透鏡的焦距由下面這個造鏡者公式決定(在此我們並不證明這個公式的由來): \[\dfrac{1}{f}=(\dfrac{n'}{n}-1) - (\dfrac{1}{R} - \dfrac{1}{R'}) \] 公式中的\(n, \, n'\)分別代表透鏡外側的折射率\(n\)和透鏡本身的折射率\(n'\)。曲率半徑\(R\)帶有符號,對於透鏡左側的凸面鏡曲率半徑\(R \gt 0\),透鏡左側的凹面鏡曲率半徑\(R \lt 0\),透鏡右側的凸面鏡曲率半徑\(R \lt 0\),透鏡右側的凹面鏡曲率半徑\(R \gt 0\)。
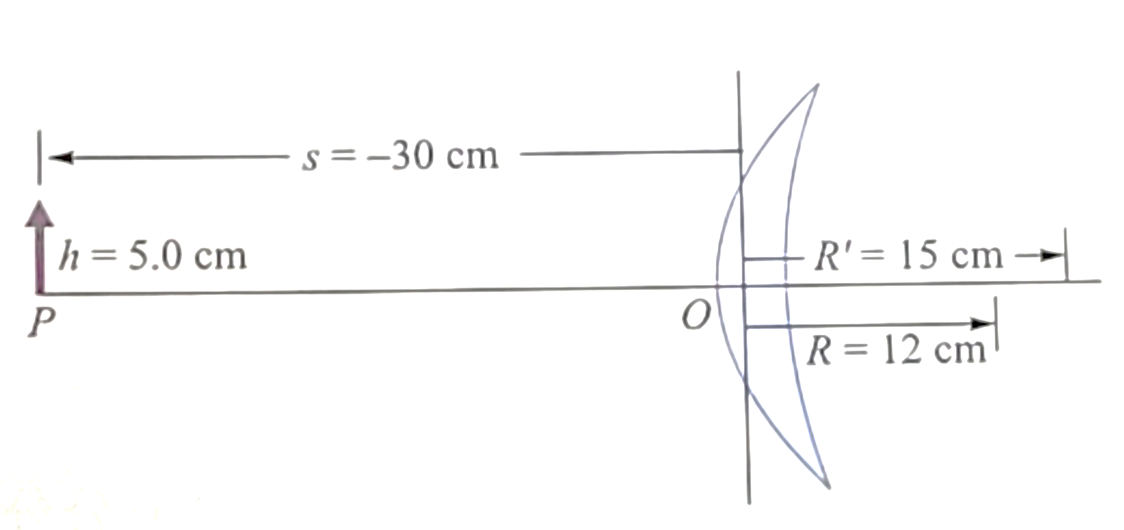 例如在右圖中我們呈現了一個凹凸透鏡,透鏡本身的折射率是1.5,其兩側的曲率半徑分別是12 cm(left)和15 cm (right),根據我們的造鏡者公式我們可以得到這個凹凸透鏡的焦距如下
例如在右圖中我們呈現了一個凹凸透鏡,透鏡本身的折射率是1.5,其兩側的曲率半徑分別是12 cm(left)和15 cm (right),根據我們的造鏡者公式我們可以得到這個凹凸透鏡的焦距如下 \(\dfrac{1}{f}=(\dfrac{n'}{n}-1) - (\dfrac{1}{R} - \dfrac{1}{R'})\)
\( =(\dfrac{1.5}{1}-1) - (\dfrac{1}{12} - \dfrac{1}{15})=\dfrac{1}{120}\)
\(f=120 \, \text{cm} \gt 0 \rightarrow 這是一個匯聚透鏡\)
光線描跡法
要決定透鏡的成像可以仿照球面鏡的光線描跡法,畫出兩條光線,而由其交點決定像點。通常可選擇以下三個光線以簡化求像的過程。- 入射線平行於主軸,則出射線或出射線的延伸線必通過焦點。
- 入射線或入射線的延伸線過焦點時,其出射線必平行於主軸。
- 入射線如通過透鏡中心則出射線不偏向。
使用描跡法,我們在下圖中顯示薄透鏡成像性質如何隨物體位置而改變。
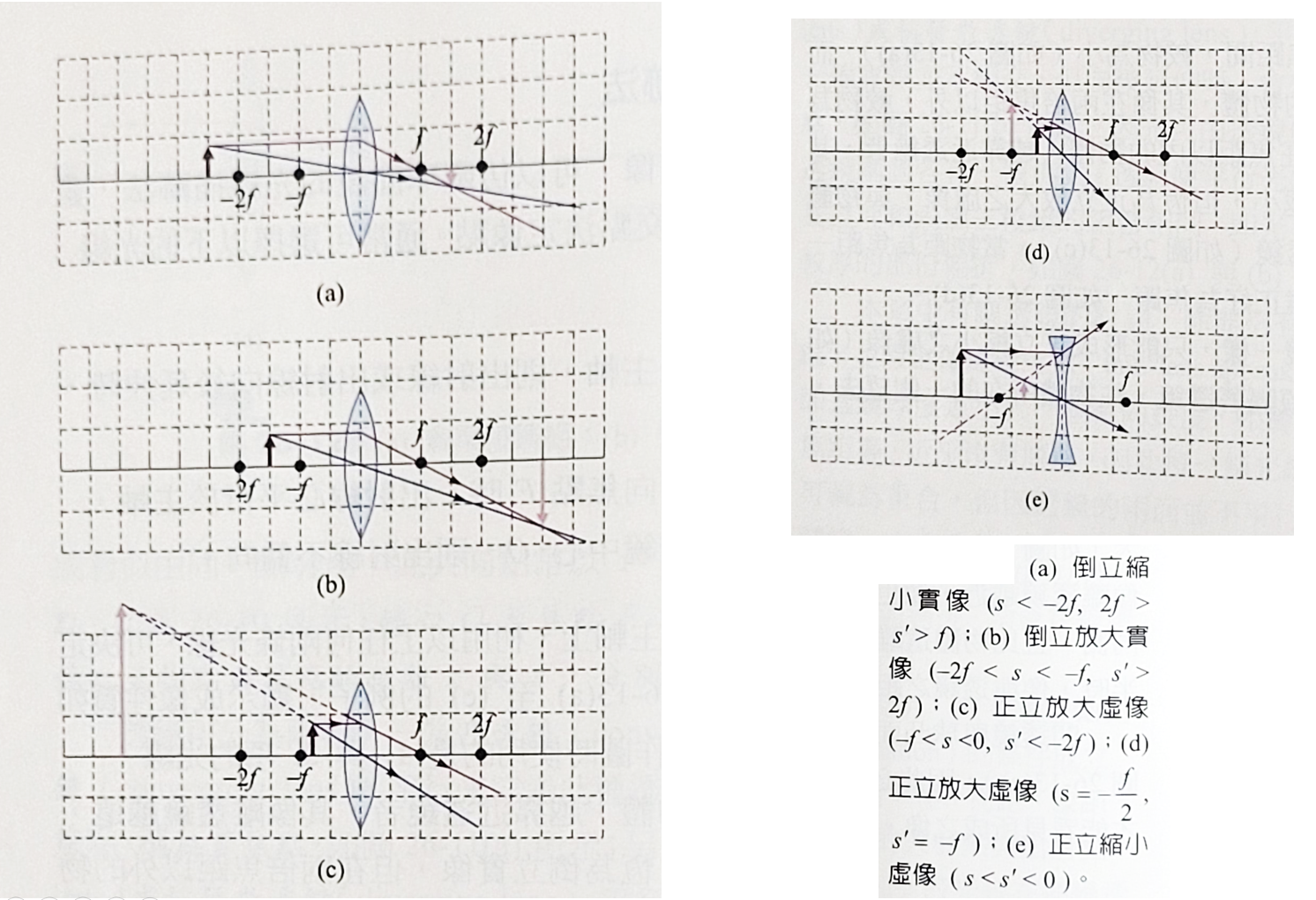
我們不難發現上圖中所有成像的位置、方向和性質,都可以用下面這個高斯公式的計算得到: \[\dfrac{1}{f}=\dfrac{1}{s'}-\dfrac{1}{s}; \quad \dfrac{1}{s'}=\dfrac{1}{f}+\dfrac{1}{s}\] \[m=\dfrac{s'}{s}\]
- \(s \lt -2f; \rightarrow f \lt s' \lt 2f; \quad m=\dfrac{s'}{s}; m \lt 0; \,\, |m| \lt 1; 倒立縮小實像\)
- \(s=-2f; \rightarrow s'=2f; \quad m=\dfrac{2f}{-2f}=-1; m \lt 0; \,\, |m|=1;倒立實像\)
- \(-2f \lt s \lt -f; \rightarrow 0 \lt s' \lt f; \quad m=\dfrac{s'}{s}; m \lt 0; \,\, |m| \gt 1; 倒立放大實像\)
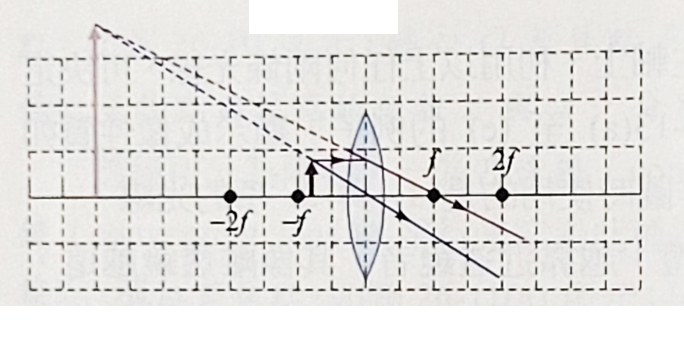
- \(-f \lt s \lt 0; \rightarrow s' \lt -2f; \quad m=\dfrac{s'}{s}; m \gt 0; \,\, |m| \gt 1; 直立放大虛像\)
對於上面例題的凹凸透鏡(f=120 cm),我們可以計算圖中物體成像的位置、方向和性質:
\(以下的推導中長度的單位是公分:s=-30; \, h=5\)
\(\dfrac{1}{s'}=\dfrac{1}{f}+\dfrac{1}{s}=\dfrac{1}{120} + \dfrac{1}{-30}=\dfrac{-1}{40}, \rightarrow s'=-40\)
\(s' \lt 0, \rightarrow 透鏡成像在左方,因此是正立的虛像\)
\(m=\dfrac{s'}{s}=\dfrac{-40}{-30}=\dfrac{4}{3}=1.333 \rightarrow 正立放大的虛像\)
\(h'=h \times m=5 \times (+4/3)=+6.7; \rightarrow 正立\)
\(\dfrac{1}{s'}=\dfrac{1}{f}+\dfrac{1}{s}=\dfrac{1}{120} + \dfrac{1}{-30}=\dfrac{-1}{40}, \rightarrow s'=-40\)
\(s' \lt 0, \rightarrow 透鏡成像在左方,因此是正立的虛像\)
\(m=\dfrac{s'}{s}=\dfrac{-40}{-30}=\dfrac{4}{3}=1.333 \rightarrow 正立放大的虛像\)
\(h'=h \times m=5 \times (+4/3)=+6.7; \rightarrow 正立\)
眼睛與眼鏡
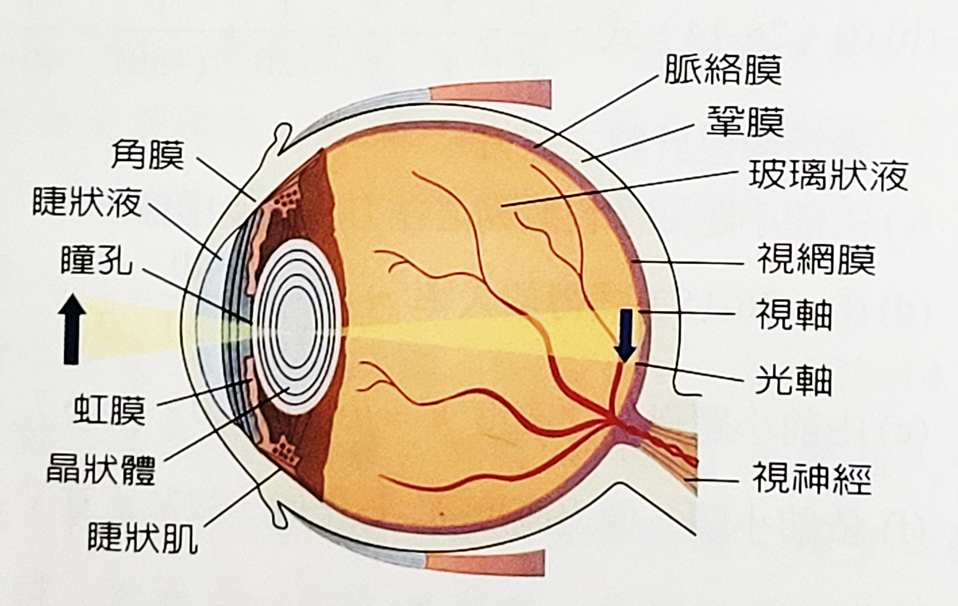 人的眼睛大致是一個直徑約2.3公分的圓求,主要構造與折射參數i
人的眼睛大致是一個直徑約2.3公分的圓求,主要構造與折射參數i
半徑(cm) 厚度(mm) n
角膜 8 0.6 1.376
水狀液 -- -- 1.336
玻璃狀液 -- -- 1.336
晶狀體 前10後6 4 1.42
正常的人眼如虹膜能隨視眼的明暗自動調節瞳孔開口的大小,直徑約2到8 mm,以增減進入眼睛的光亮,而其睫狀肌則隨注視點的遠近,自動調整晶狀體表面的彎曲度,使景物在視網膜上的黃斑中凹處,形成清楚的倒立縮小實像,刺激視覺細胞,再經由視神經將訊息傳至腦部,引發視覺。 角膜與晶狀體的折射率分別是1.38與1.42,相對於水狀液與玻璃狀液其比值分別為1.03與1.06,但角膜相對於空氣的折射率則較大,約為1.376,因此進入人員的光線,其折射偏向主要來自角膜,而非眼睛內部。儘管如此,藉由睫狀肌的收縮,晶狀體所產生的焦距改變,卻可讓大約在眼前25公分之外至無窮遠處的景物,清楚成像於網膜上。眼前景物必須成像於網膜上,眼睛才能看得清楚,稱為明視。當睫狀肌放鬆時晶狀體的形狀較為扁平,其焦距較長,此時正長人眼睛正好能將無窮遠處的景物成像於視網膜上。但其他較近的景物,其像距較長,成像落於視網膜後而無法明視。因此睫狀肌必須收縮,以增加晶狀體的曲率,使眼睛的焦距縮短,才能使近處景物可以成像於視網膜上,這稱為眼睛的調節作用。只靠調節作用正常人眼的明視距離最遠為無窮遠處,稱為明視的遠點,而最近則約可在眼前25公分處,稱為明視的近點。隨著年齡增加,人眼的調節作用漸漸變差,明視近點會逐漸變遠,而看不清楚近距離的景物,稱為老花眼。 要補救此種視力缺失,必須佩戴匯聚透鏡,以使正常人的近點的景物,成像於佩戴者的近點處。如果老花眼者的近點為2.0公尺,那麼根據公式的計算 (長度的單位是公尺) \[曲光度,D=\dfrac{1}{f}=\dfrac{1}{s'}-\dfrac{1}{s}=\dfrac{1}{-2.0} - \dfrac{1}{-0.25}=+3.5\] 需配戴的眼鏡的焦距(f=1/3.5)與折射本領約為\(D=3.5\),因為眼睛度數為曲光度的100倍,所以+3.5曲光度相當於正350度。
遠視眼的眼睛,角膜視網膜的距離校正常者短,當睫狀肌放鬆時無窮遠處的景物成像於網膜後,如要產生明視可靠調節作用,使晶狀體與眼睛的焦距縮短。但景物越近時,成像離網越遠,而調節作用有一定的極限,所以景物接近到某一距離時,遠視者的眼睛即無法明視,此距離即為其明視近點。遠視眼者之近點較正常人遠,這點和老花眼並無不同,因此遠視眼矯正視力時所配戴的眼鏡與老花眼相同。
放大鏡與顯微鏡
 如左圖所示當物體在凸透鏡的焦點以內時,會出現正立放大的虛像,也就是像高h'與物高h之比,\(|m| \gt 1\),但凸透鏡可以當作放大鏡,其判斷的依據並不是因為所成之像較物為大。人眼依據視覺判斷兩物體誰大誰小時,其實比較的不是物和像的實際大小,而是兩物體在視網膜上成像的大小(如右圖)。
如左圖所示當物體在凸透鏡的焦點以內時,會出現正立放大的虛像,也就是像高h'與物高h之比,\(|m| \gt 1\),但凸透鏡可以當作放大鏡,其判斷的依據並不是因為所成之像較物為大。人眼依據視覺判斷兩物體誰大誰小時,其實比較的不是物和像的實際大小,而是兩物體在視網膜上成像的大小(如右圖)。
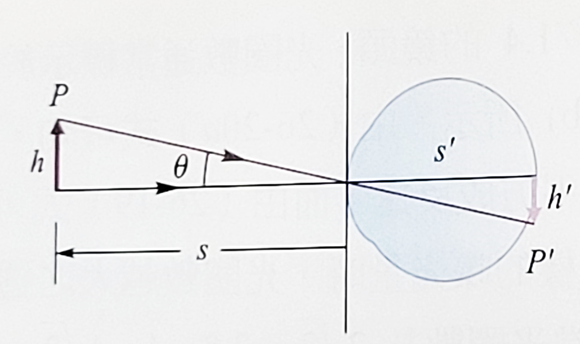 如果物\(P\)在視網膜上的像為\(P'\),那麼根據公式,像的高度與物的高度的比值為
\[ m=\dfrac{h'}{h}=\dfrac{s'}{n"} \cdot \dfrac{n}{s}=\dfrac{k}{s}; \quad k=\dfrac{s' n}{n"}\]
公式中的\(s'\)為角膜到網膜的距離,不隨物體與物距而變,所以這是一個大於0的常數。因為人眼看到物體,其大小由\(h'\)決定,
\[h'=k\dfrac{h}{s}=k \tan \theta \simeq k\theta \]
由這個公式我們得到所以人眼看得物體其大小由物體對眼睛之張角決定,放大鏡的放大率指的是經由與不經由凸透鏡明視一物體時,視網膜上的像高,增大的倍數。經由凸透鏡時人員在明視下看到的物,其實是物體經過凸透鏡所成的虛像\(P'\),因此必須出現在明視距離。不經由凸透鏡時,人眼在明視下看到的物,則是位在明視距離的\(P'\)。請注意正常人員可以明視的\(P'\)或\(P_n\),其標準範圍是眼前25公分到無窮遠處。
如果物\(P\)在視網膜上的像為\(P'\),那麼根據公式,像的高度與物的高度的比值為
\[ m=\dfrac{h'}{h}=\dfrac{s'}{n"} \cdot \dfrac{n}{s}=\dfrac{k}{s}; \quad k=\dfrac{s' n}{n"}\]
公式中的\(s'\)為角膜到網膜的距離,不隨物體與物距而變,所以這是一個大於0的常數。因為人眼看到物體,其大小由\(h'\)決定,
\[h'=k\dfrac{h}{s}=k \tan \theta \simeq k\theta \]
由這個公式我們得到所以人眼看得物體其大小由物體對眼睛之張角決定,放大鏡的放大率指的是經由與不經由凸透鏡明視一物體時,視網膜上的像高,增大的倍數。經由凸透鏡時人員在明視下看到的物,其實是物體經過凸透鏡所成的虛像\(P'\),因此必須出現在明視距離。不經由凸透鏡時,人眼在明視下看到的物,則是位在明視距離的\(P'\)。請注意正常人員可以明視的\(P'\)或\(P_n\),其標準範圍是眼前25公分到無窮遠處。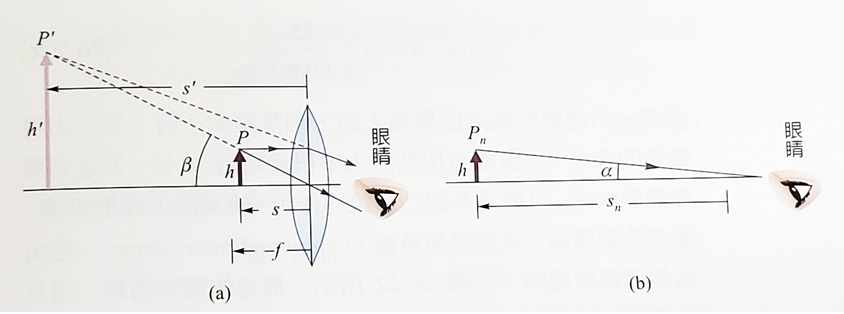
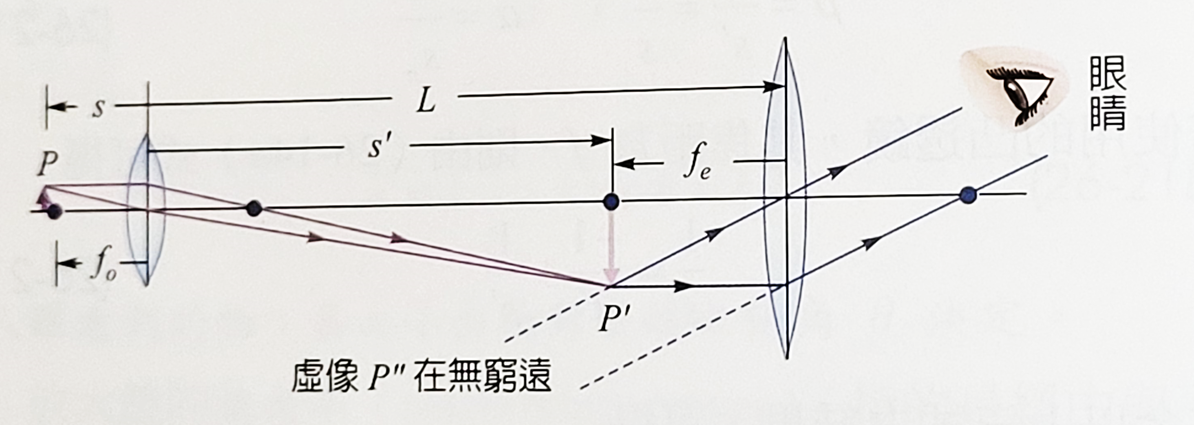 靠近物體的透鏡稱為物鏡,能使恰好位於其焦距\(f_o\)外之物體\(P\),形成放大之倒立實像\(P'\)。另一個透鏡靠近人眼,稱為目鏡。實像\(P'\)剛好位於目鏡焦距\(f_e\)之內,人眼透過目鏡看到的則為,以\(P'\)為物的放大虛像\(P"\)。這個虛像位於人眼明視的遠點,也就是無窮遠處。物鏡與目鏡的焦距都相當短,所以可視為遠小於物鏡到目鏡的距離\(L\)
\[f_o \ll L; \quad f_e \ll L\]
\(P\)位於物鏡焦點外,因此物靜的橫向放大率為
\[m_o=\dfrac{s'}{s} \simeq \dfrac{s'}{-f_o}; \quad s'=L-f_e \simeq L \rightarrow m_o \simeq \dfrac{L}{-f_o}\]
人眼由目鏡看實像\(P'\)正如同以目鏡為放大率的情況,因此又得到根據目鏡的放大率公式可得
\[m_{\theta}=\dfrac{25}{f_e}\]
所以最後我們可以計算出顯微鏡的放大率是
\[m=m_o m_{\theta}=-\dfrac{L}{f_o} \cdot \dfrac{25}{f_e}\]
上面的公式中放大率是負的,也就是人眼看到的是倒立虛像,而為了提高放大率物鏡目鏡都選用焦距很短的凸透鏡。
靠近物體的透鏡稱為物鏡,能使恰好位於其焦距\(f_o\)外之物體\(P\),形成放大之倒立實像\(P'\)。另一個透鏡靠近人眼,稱為目鏡。實像\(P'\)剛好位於目鏡焦距\(f_e\)之內,人眼透過目鏡看到的則為,以\(P'\)為物的放大虛像\(P"\)。這個虛像位於人眼明視的遠點,也就是無窮遠處。物鏡與目鏡的焦距都相當短,所以可視為遠小於物鏡到目鏡的距離\(L\)
\[f_o \ll L; \quad f_e \ll L\]
\(P\)位於物鏡焦點外,因此物靜的橫向放大率為
\[m_o=\dfrac{s'}{s} \simeq \dfrac{s'}{-f_o}; \quad s'=L-f_e \simeq L \rightarrow m_o \simeq \dfrac{L}{-f_o}\]
人眼由目鏡看實像\(P'\)正如同以目鏡為放大率的情況,因此又得到根據目鏡的放大率公式可得
\[m_{\theta}=\dfrac{25}{f_e}\]
所以最後我們可以計算出顯微鏡的放大率是
\[m=m_o m_{\theta}=-\dfrac{L}{f_o} \cdot \dfrac{25}{f_e}\]
上面的公式中放大率是負的,也就是人眼看到的是倒立虛像,而為了提高放大率物鏡目鏡都選用焦距很短的凸透鏡。
望遠鏡
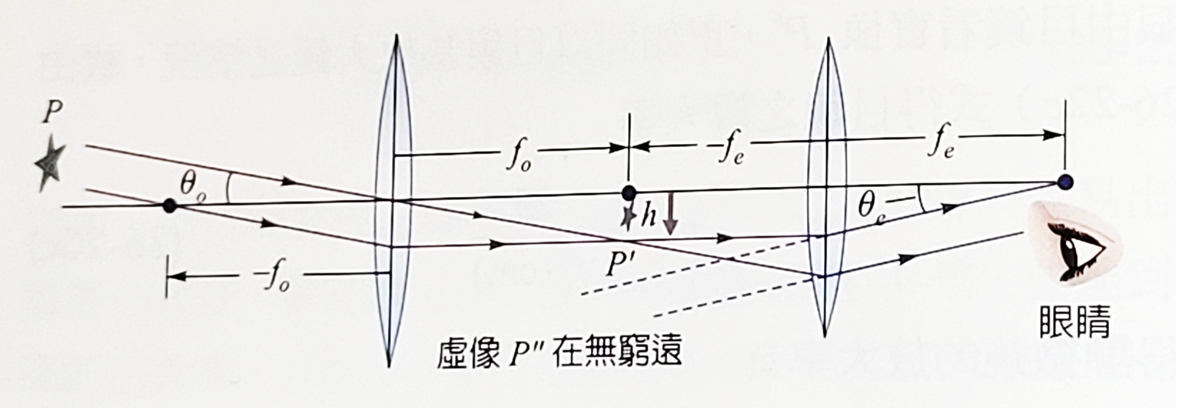 望遠鏡可收集來自遠方物體的光,以便成像供觀察者檢視或供其他儀器分析之用。望遠鏡依其收集光時,主要是採用折射透鏡或反射面鏡,可分為折射式與反射式兩類。手持型和雙筒望遠鏡、遠距照相機的鏡頭以及老式的望遠鏡,通常為折射式,現代的天文望遠鏡則多為反射式。將一個凸透鏡當作物鏡,可將遠方的物體成像於其焦點附近,因此凸透鏡可說是最簡單的折射望遠鏡。但若以另一凸透鏡為目鏡,物鏡所成之實像恰位於目鏡焦點內,則如前述顯微鏡之目鏡,人眼將能以高倍之角放大率,看到位於無窮遠處之虛像。因此這種具有物鏡與目鏡的望遠鏡與顯微鏡成像原理基本上是相同的,不過為了盡量多收起來自遠方的光,望遠鏡的物鏡需具有較大的孔徑。為了提高角放大率,也需具有較長的焦距,這點可以有下面的分析看出來。
望遠鏡可收集來自遠方物體的光,以便成像供觀察者檢視或供其他儀器分析之用。望遠鏡依其收集光時,主要是採用折射透鏡或反射面鏡,可分為折射式與反射式兩類。手持型和雙筒望遠鏡、遠距照相機的鏡頭以及老式的望遠鏡,通常為折射式,現代的天文望遠鏡則多為反射式。將一個凸透鏡當作物鏡,可將遠方的物體成像於其焦點附近,因此凸透鏡可說是最簡單的折射望遠鏡。但若以另一凸透鏡為目鏡,物鏡所成之實像恰位於目鏡焦點內,則如前述顯微鏡之目鏡,人眼將能以高倍之角放大率,看到位於無窮遠處之虛像。因此這種具有物鏡與目鏡的望遠鏡與顯微鏡成像原理基本上是相同的,不過為了盡量多收起來自遠方的光,望遠鏡的物鏡需具有較大的孔徑。為了提高角放大率,也需具有較長的焦距,這點可以有下面的分析看出來。如圖所示因物\(P\)位於無窮遠處,故在望遠鏡所在位置,以人眼直接觀看之張角約為 \[\theta_o = \dfrac{h}{-f_o}\] 而透過目鏡所看到的虛像\(P"\)位於無窮遠處,其張角為 \[\theta_e=\dfrac{h}{f_e}\] 所以望遠鏡的放大率是 \[m_{\theta}=\dfrac{\theta_e}{\theta_o}=-\dfrac{f_o}{f_e}\] 上面這個公式中顯示,放大率隨物鏡的焦距變長而增大,而放大率為負的,表示人眼所看到的像是倒立虛像。所以這種望遠鏡用在觀察地面景物時,都需加裝能使影像倒轉之光學裝置,例如伽利略設計的望遠鏡,最初就是以凹透鏡做為目鏡;雙筒望遠鏡則常加裝全反射稜鏡。就天文研究而言,望遠鏡所成之像是否為正立無關緊要,放大率是高低也不是特別重要,較值得重視的其實是收集光的能力,也就是物鏡的孔徑大小。反射式望遠鏡有許多優點,例如因為不牽涉到光的折射,不會出現色散問題,只用單一面,反射鏡面的背面全部可以用來安裝支持鏡體重量或改變鏡面曲率的裝置。故反射鏡面的面積不僅可以很大,其曲率也可以視需要改變,而能發揮最佳的聚焦功能。全世界最大的反射式望鏡直徑達10公尺,哈伯望遠鏡的直徑也有2.4公尺,相形之下折射望遠鏡因為只有其邊緣可利用來做支持重量,所以孔徑較受限制,最大的折射望遠鏡其直徑也不過1公尺。
例題
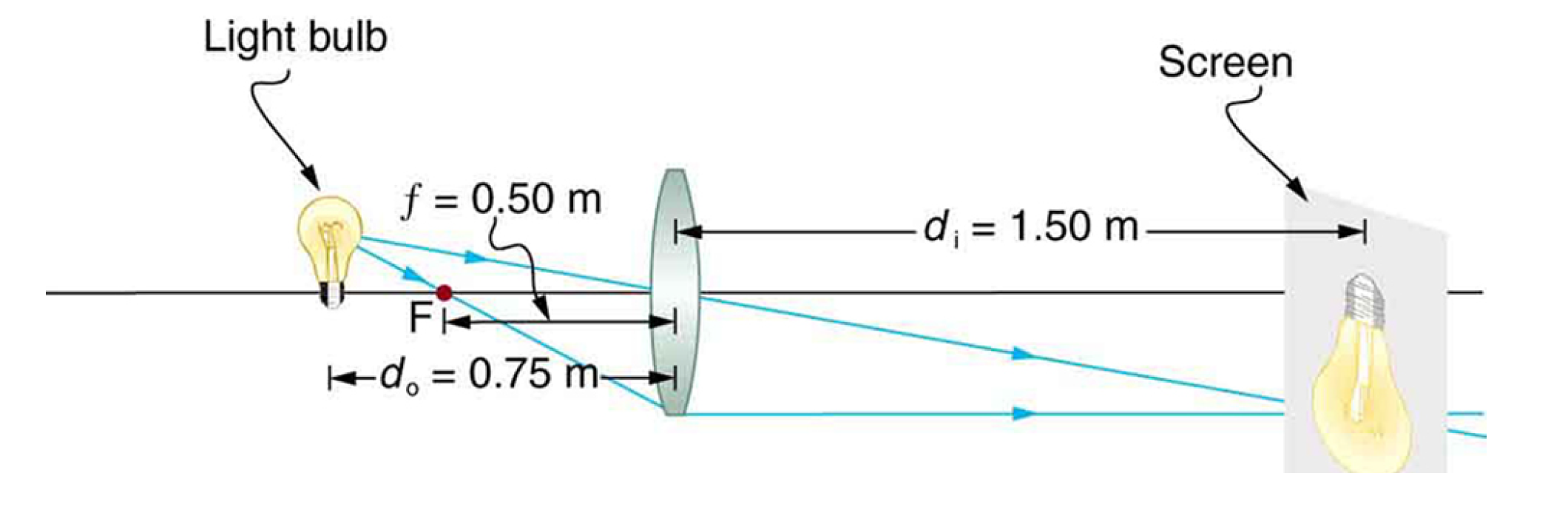
HL34例題-1
A tarantula of height \(h\) sits cautiously before a spherical mirror whose focal length has absolute value \(|f|= 40\) cm. The image of the tarantula produced by the mirror has the same orientation as the tarantula and has height \(h'=0.2h\). (a) Is the image real or virtual, and is it on the same side of the mirror as the tarantula or the opposite side? (b) Is the mirror concave or convex, and what is its focal length \(f\), sign included?
一隻高度為 \(h\) 的狼蛛小心地坐在焦距絕對值為 \(|f|= 40\) cm 的球面鏡前。 鏡子產生的狼蛛圖像與狼蛛的方向相同,高度為\(h'=0.2h\)。 (a)其像是實像的還是虛像,它是與狼蛛在鏡子的同一側還是相反的一側? (b) 鏡子是凹的還是凸的,它的焦距是多少\(f\)(包含符號)?
(a)因為像與狼蛛(物體)具有相同的方向,所以它必然是虛像,並且位於鏡子的另一側。
(b)
\(|m|=\dfrac{h'}{h}=0.2\)
\(\dfrac{i}{p}=-0.2; \quad i=-0.2 p\)
\(\dfrac{1}{f}=\dfrac{1}{i}+\dfrac{1}{p}=\dfrac{1}{-0.2p}+{1}{p}=\dfrac{-4}{p}\)
\(f=-p/4\)
因為\(p\)是正的,所以\(f\)一定是負的,也就是說鏡子是凸的,\(|f|=40 \, cm \rightarrow f=-40 \, cm\)。
一隻高度為 \(h\) 的狼蛛小心地坐在焦距絕對值為 \(|f|= 40\) cm 的球面鏡前。 鏡子產生的狼蛛圖像與狼蛛的方向相同,高度為\(h'=0.2h\)。 (a)其像是實像的還是虛像,它是與狼蛛在鏡子的同一側還是相反的一側? (b) 鏡子是凹的還是凸的,它的焦距是多少\(f\)(包含符號)?
(a)因為像與狼蛛(物體)具有相同的方向,所以它必然是虛像,並且位於鏡子的另一側。
\(|m|=\dfrac{h'}{h}=0.2\)
\(\dfrac{i}{p}=-0.2; \quad i=-0.2 p\)
\(\dfrac{1}{f}=\dfrac{1}{i}+\dfrac{1}{p}=\dfrac{1}{-0.2p}+{1}{p}=\dfrac{-4}{p}\)
\(f=-p/4\)
因為\(p\)是正的,所以\(f\)一定是負的,也就是說鏡子是凸的,\(|f|=40 \, cm \rightarrow f=-40 \, cm\)。
HL34例題-2
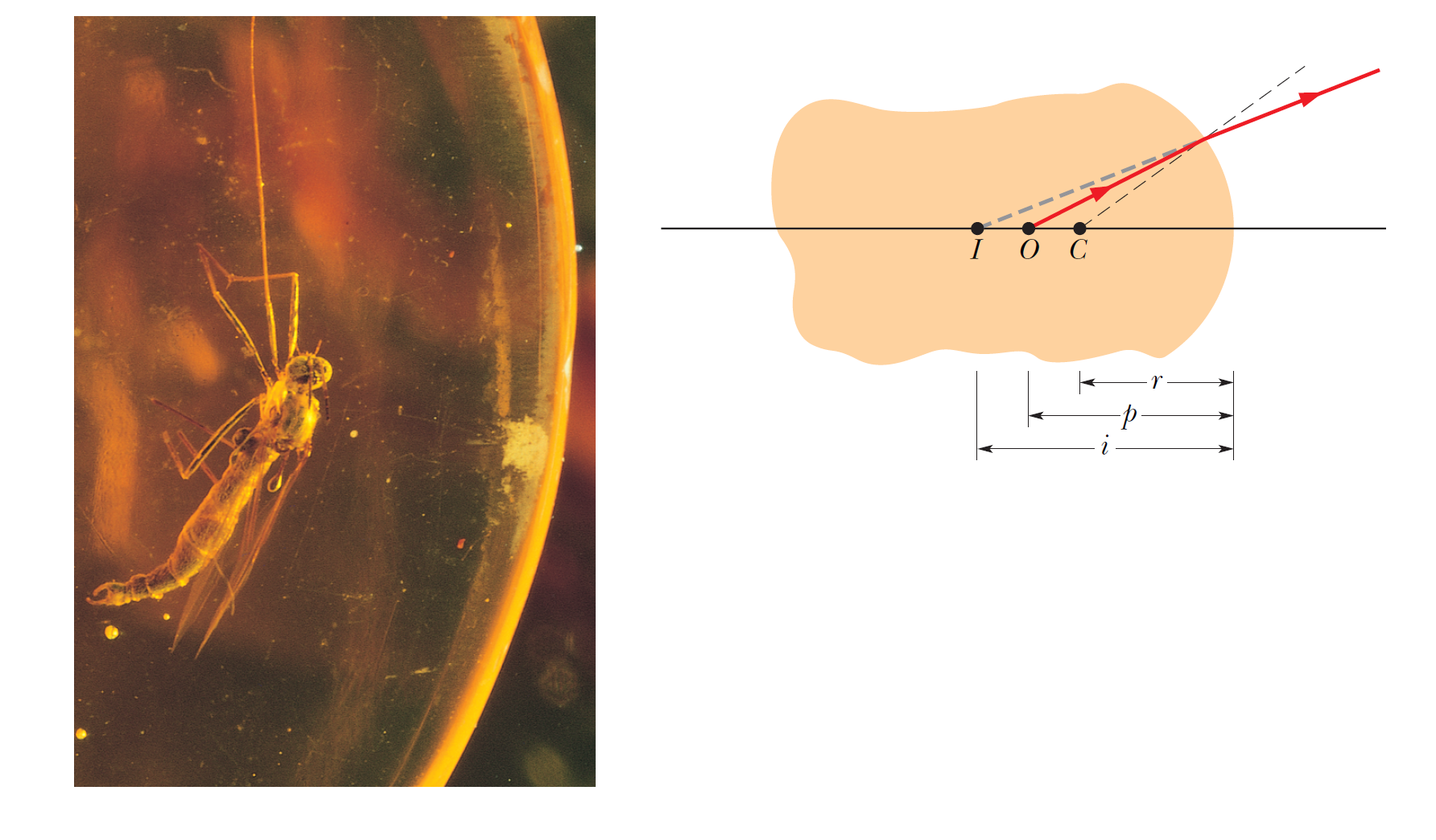 A Jurassic mosquito is discovered embedded in a chunk of amber, which has index of refraction 1.6. One surface of the amber is spherically convex with radius of curvature 3.0 mm. The mosquito's head happens to be on the central axis of that surface and, when viewed along the axis, appears to be buried 5.0 mm into the amber. How deep is it really?
A Jurassic mosquito is discovered embedded in a chunk of amber, which has index of refraction 1.6. One surface of the amber is spherically convex with radius of curvature 3.0 mm. The mosquito's head happens to be on the central axis of that surface and, when viewed along the axis, appears to be buried 5.0 mm into the amber. How deep is it really? 一隻侏羅紀蚊子被發現嵌在一塊折射率為 1.6 的琥珀中。 琥珀的一個表面呈球形凸面,曲率半徑為 3.0 mm。 蚊子的頭部恰好位於該表面的中心軸上,當沿軸觀察時,它似乎被埋在琥珀中 5.0 毫米處。 到底有多深?
頭部似乎在琥珀中 5.0 毫米,只是因為觀察者截獲的光線在凸起的琥珀表面處被折射彎曲。 像距 \(i\) 與物距 \(p\) 必須滿足的公式: \(\dfrac{n_1}{p}+\dfrac{n2}{i}=\dfrac{n_2-n_1}{r}\)。 要使用該方程求物距,我們首先要注意:
- 因為物體(頭部)和它的圖像在折射面的同一側,所以像必須是虛像,所以 \(i=-5.0\) 毫米。
- 因為物體總是被認為是在折射率介質\(n_1\),我們必須有\(n_1 = 1.6\) 和\(n_2 = 1.0\)。
- 由於物體面對凹折射面,曲率半徑\(r\)為負,所以\(r=-3.0\) mm。
\(\dfrac{n_1}{p}+\dfrac{n2}{i}=\dfrac{n_2-n_1}{r}\)
\(\dfrac{1.6}{p}+\dfrac{1.0}{-5 \, mm}=\dfrac{1.0-1.6}{-3.0 \, mm}\)
\(p=4.0 \, mm\)
HL34例題-3
螳螂沿著一個薄的對稱鏡片的中軸捕食,距鏡片20厘米。鏡片提供的螳螂橫向放大率為\(m =-0.25\),鏡片材料的折射率為1.65。 (a) 確定鏡頭產生的圖像類型,鏡頭類型,物體(螳螂)是在焦點之內還是之外,圖像出現在鏡頭的哪一側,圖像是否倒置。 (b) 透鏡的兩個曲率半徑是多少?
(a)
我們可以從給定的\(m\)值中了解很多關於鏡頭和圖像的信息。從它和\(m=-i/p\),我們看到\(i=-mp=0.25p\)。即使沒有完成計算,我們也可以回答問題。因為 \(p\) 是正數,所以這裡的\(i\)一定是正數。這意味著我們有一個實像,我們有一個會聚鏡頭(唯一可以產生實像的鏡頭)。物體必須在焦點之外(生成實像的唯一方法)。此外,像是倒置的,位於與物體相對的鏡頭一側。
(b)
\(i=(0.25)(20)=5.0 \, cm\)
\(\dfrac{1}{f}=\dfrac{1}{p}+\dfrac{1}{i}=\dfrac{1}{20}+\dfrac{1}{5}\)
\(f=4.0 \, cm\)
\(r_1=r; \quad r_2=-r\)
\(\dfrac{1}{f}=(n-1)\left( \dfrac{1}{r_1} - \dfrac{1}{r_2}\right)=(n-1)\left( \dfrac{1}{+r}-\dfrac{1}{-r}\right)\)
\(\dfrac{1}{4.0}=(1.65-1)\dfrac{2}{r} \Rightarrow r=(0.65)(2)(4.0)=5.2 \, cm\)
(a)
我們可以從給定的\(m\)值中了解很多關於鏡頭和圖像的信息。從它和\(m=-i/p\),我們看到\(i=-mp=0.25p\)。即使沒有完成計算,我們也可以回答問題。因為 \(p\) 是正數,所以這裡的\(i\)一定是正數。這意味著我們有一個實像,我們有一個會聚鏡頭(唯一可以產生實像的鏡頭)。物體必須在焦點之外(生成實像的唯一方法)。此外,像是倒置的,位於與物體相對的鏡頭一側。
(b)
\(i=(0.25)(20)=5.0 \, cm\)
\(\dfrac{1}{f}=\dfrac{1}{p}+\dfrac{1}{i}=\dfrac{1}{20}+\dfrac{1}{5}\)
\(f=4.0 \, cm\)
\(r_1=r; \quad r_2=-r\)
\(\dfrac{1}{f}=(n-1)\left( \dfrac{1}{r_1} - \dfrac{1}{r_2}\right)=(n-1)\left( \dfrac{1}{+r}-\dfrac{1}{-r}\right)\)
\(\dfrac{1}{4.0}=(1.65-1)\dfrac{2}{r} \Rightarrow r=(0.65)(2)(4.0)=5.2 \, cm\)
HL34例題-4
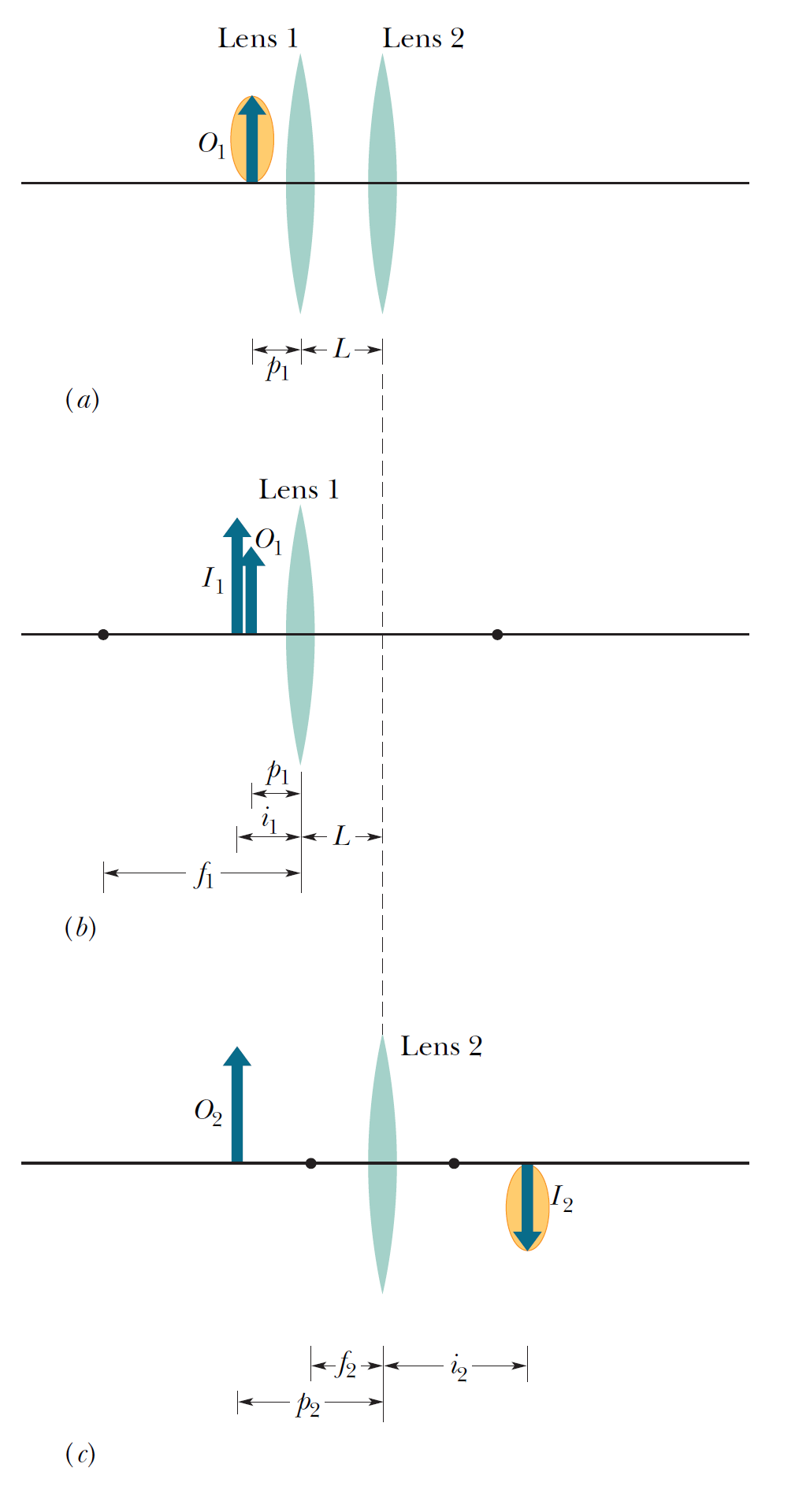 右圖顯示了一個墨西哥胡椒種子 \(O_1\),它放置在兩個薄對稱同軸透鏡 1 和 2 的前面,焦距分別為 \(f_1=+24\) cm 和 \(f2=+9.0\) cm ,並且透鏡間距為 \(L =10\) cm。 種子距離鏡頭-1 6.0 cm。兩個鏡頭的系統會在哪裡產生種子的像?
右圖顯示了一個墨西哥胡椒種子 \(O_1\),它放置在兩個薄對稱同軸透鏡 1 和 2 的前面,焦距分別為 \(f_1=+24\) cm 和 \(f2=+9.0\) cm ,並且透鏡間距為 \(L =10\) cm。 種子距離鏡頭-1 6.0 cm。兩個鏡頭的系統會在哪裡產生種子的像? 我們可以通過跟蹤來自種子的光線穿過兩個透鏡,來定位透鏡系統產生的像。但是,我們可以通過逐個鏡頭逐步完成系統來計算該像的位置。我們從靠近種子的鏡頭開始。我們最終要找的像是鏡頭-2產生的像\(I_2\)。
透鏡-1:
忽略透鏡-2,我們定位\(I_1\)的像。透鏡-1的成像公式:
\[\dfrac{1}{p_1}+\dfrac{1}{i_1}=\dfrac{1}{f_1} \\ p_1=+6 \,cm, f_1=+24\, cm \\ \Rightarrow i_1=-8\, \text{cm}\] 透鏡-1成像的圖形如右圖(b)所顯示的。
透鏡-2:
在我們的第2步中,我們將像\(I_1\)視為第2個透鏡的物體\(O_2\),現在忽略透鏡-1(如右圖(c))。我們首先注意到這個物體\(O_2\)在透鏡-2的焦點外面。所以透鏡-2產生的像\(I_2\)必須是實像、倒置的,並且在透鏡-2的\(O_2\)的一側。
\(p_2=L+|i_1|=18 \, cm; \quad \dfrac{1}{+18}+\dfrac{1}{i_2}=\dfrac{1}{+9} \Rightarrow i_2=+18 \, 厘米\)
\(i_2\)的"+"號證實了我們的猜測:由透鏡-2產生的像\(I_2\)是實像、倒置的,並且在透鏡-2 的對面 \(O_2\) 的一側,如圖(c)所示。
授課教師
陳永忠 ycchen@thu.edu.tw