波動光學1-干涉
在前一個單元由幾何光學的觀點,探討光在介面的反射與折射現象,除了說明其必須遵循的基本定律外,也介紹其在成像問題上的應用。幾何光學是一種近似的理論,並不適合用在光經由其波動性質而實現的一些特有現象上,因此本單元改由物理光學的觀點,來探討光的波動現象,並將重點放在物理光學中一再出現的兩個基本現象,那就是干涉與繞射。物理學的主要目標之一是了解光的本質。由於光很複雜,這個目標一直難以實現。然而,這種複雜性也造就了許多應用機會,其中一些最豐富的應用涉及光波的干涉。大自然長期以來一直使用光學干涉來展現豐富的色彩,例如大閃蝶的翅膀是暗淡的、從翅膀底部的表面可以看出其平淡無奇的棕色,但由於從該表面反射的光的干涉,棕色被一種引人注目的藍色隱藏在頂部表面。此外,頂面具有多變的顏色;如果您改變視角或當翅膀移動時,顏色的色調就會改變。許多貨幣的墨水中使用了類似的顏色偏移來防止偽造。影印機只能從一個角度複製顏色,因此無法複製由各種角度變化引起的相應的顏色偏移。在我們討論蝴蝶翅膀和貨幣墨水的顏色變化之前,我們首先必須討論光學干涉的基本物理學。為了解釋干涉現象,我們必須放棄幾何光學(我們將光描述為光線)的簡單性,回到光的波動本質上。再下一個單元中我們再來探討光波的另一個重要性質--繞射。
相干性與干涉
當電場與磁場以波動的方式傳播,且波長約在400至700奈米的範圍時,就形成可見光波,或稱為光波。光波與其他電磁波的干涉與力學波基本上是相同的,在上學期普通物理一的課程中我們介紹了力學波的波動學,例如水波的介質是水,透過描述水面的位移來描述水波。課程中我們討論過兩個力學波重疊時,其合成波的位移量與兩波之間的相位差有關,有可能出現相長與相消的干涉。光波傳遞時不需要介質所以是非力學波,光波的電場和磁場相當於力學波的位移,也是用波的重疊原理,兩光波重疊時合成波的電場等於個別波的電場,以向量加法相加得到的總和。所以兩光波出現相長干涉時,合成波的電場增強,反之二光波出現相消干涉時,合成波的電場減弱。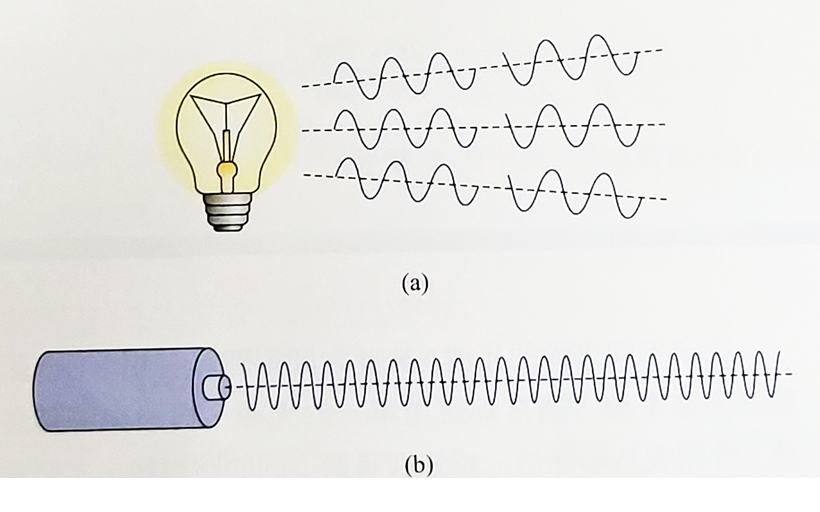 雖然兩個波相遇,就一定會產生干涉,並出現干涉圖樣,但若要圖樣維持穩定不變,則兩波必須具有相干性或同調性。也就是說兩波的相位差是固定的,不隨時間而變。一般而言太陽和白熾燈泡等是熱光源,所產生的光波都是相當短的波列,其長度只有幾個波長,而且兩個波列之間的相位差,並無一定的關係。相形之下,雷射發出的光波,每一波列均相當長,可達很多個波長。波列只有在距離小於其長度的範圍內時,才可能具有相干性。一波列自始至終的時間可視其為相干時間,而波列前後的長度可視為其相干長度。一光源的相干長度,大致與其所發出的波列長度相等,因此熾熱光源的相干長度甚短,大約就是光的波長,而雷射光源的長度就非常的長遠大於光的波長。
答曰為光的波長雷射光源的相干長度則相當長,遠大於光的波長。
雖然兩個波相遇,就一定會產生干涉,並出現干涉圖樣,但若要圖樣維持穩定不變,則兩波必須具有相干性或同調性。也就是說兩波的相位差是固定的,不隨時間而變。一般而言太陽和白熾燈泡等是熱光源,所產生的光波都是相當短的波列,其長度只有幾個波長,而且兩個波列之間的相位差,並無一定的關係。相形之下,雷射發出的光波,每一波列均相當長,可達很多個波長。波列只有在距離小於其長度的範圍內時,才可能具有相干性。一波列自始至終的時間可視其為相干時間,而波列前後的長度可視為其相干長度。一光源的相干長度,大致與其所發出的波列長度相等,因此熾熱光源的相干長度甚短,大約就是光的波長,而雷射光源的長度就非常的長遠大於光的波長。
答曰為光的波長雷射光源的相干長度則相當長,遠大於光的波長。來自不同光源的光波彼此之間很難具有相干性,因此實際的光波干涉通常都使用單一的光源,而設法將其發出的波分開成為兩部分,並分別經過不同的路徑後才交會在一起,產生干涉。當然兩路徑的長度差不可超過光源的相甘長度,否則就無法形成穩定的干涉圖案。兩光波的頻率必須相同,才能具有相干性,因此,不同波長和顏色的光,不具相干性。當兩光波的頻率相當接近時,其干涉圖樣會類似於聲波產生拍的現象,而以拍的頻率變化。雷射光源的相干長度很長,且能發出近乎單一波長的光,也就是單色光,因此用來進行干涉實驗是非常適合的。太陽和白熾燈泡發出的白光,是由不同波長的多種色光合成的,每一種色光有其各自的干涉圖樣,因此整體的干涉現象通常較為複雜,而此類光源的相干長度又甚短,因此較不利於用來進行干涉實驗。
相長與相消干涉
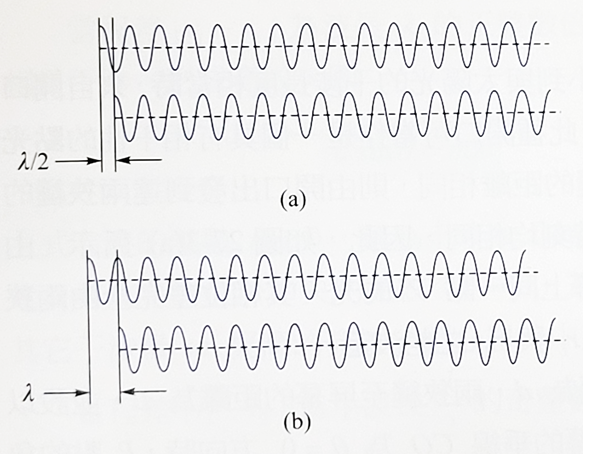 將來自同一光源的單色光波分開成為兩部分,使其通過不同路徑後重疊在一起。若兩路徑長的差,正好為半波長的奇數倍,則兩波相位差為180度,稱為異相或反相,重疊後會出現相消干涉,即合成波的波幅等於兩波波幅相減,因此光波強度減弱。如果兩波的振幅大小相同,則在相消干涉下合成波的振幅就成為0。若兩路徑長的差正好為波長的整數倍,則兩波相位差為0度或稱為同相位,重疊後會出現相長干涉。
也就是合成波的振幅等於兩波振幅相加,因此光波強度增強。CD,VCD,DVD這種類型的光碟片,能以數位化的方式儲存大量的聲音與影像訊號或電腦數據,其方法是將一具有反光性的圓形金屬平面,劃分成多個同心的圓形軌道區,並在各區打出一些深度相同的凹洞,當以照射面積稍大於凹洞的雷射光束照射時,凹洞與洞口周圍平坦部分的反射光,由於路徑長相差約為雷射光的半波長,會出現相消干涉,因此由光偵測器收到的反射光會比沒有凹洞稍微減弱,因此就可利用該處是否有凹洞來代表0和1,達到儲存數位化資料的目的。
將來自同一光源的單色光波分開成為兩部分,使其通過不同路徑後重疊在一起。若兩路徑長的差,正好為半波長的奇數倍,則兩波相位差為180度,稱為異相或反相,重疊後會出現相消干涉,即合成波的波幅等於兩波波幅相減,因此光波強度減弱。如果兩波的振幅大小相同,則在相消干涉下合成波的振幅就成為0。若兩路徑長的差正好為波長的整數倍,則兩波相位差為0度或稱為同相位,重疊後會出現相長干涉。
也就是合成波的振幅等於兩波振幅相加,因此光波強度增強。CD,VCD,DVD這種類型的光碟片,能以數位化的方式儲存大量的聲音與影像訊號或電腦數據,其方法是將一具有反光性的圓形金屬平面,劃分成多個同心的圓形軌道區,並在各區打出一些深度相同的凹洞,當以照射面積稍大於凹洞的雷射光束照射時,凹洞與洞口周圍平坦部分的反射光,由於路徑長相差約為雷射光的半波長,會出現相消干涉,因此由光偵測器收到的反射光會比沒有凹洞稍微減弱,因此就可利用該處是否有凹洞來代表0和1,達到儲存數位化資料的目的。雙狹縫干涉
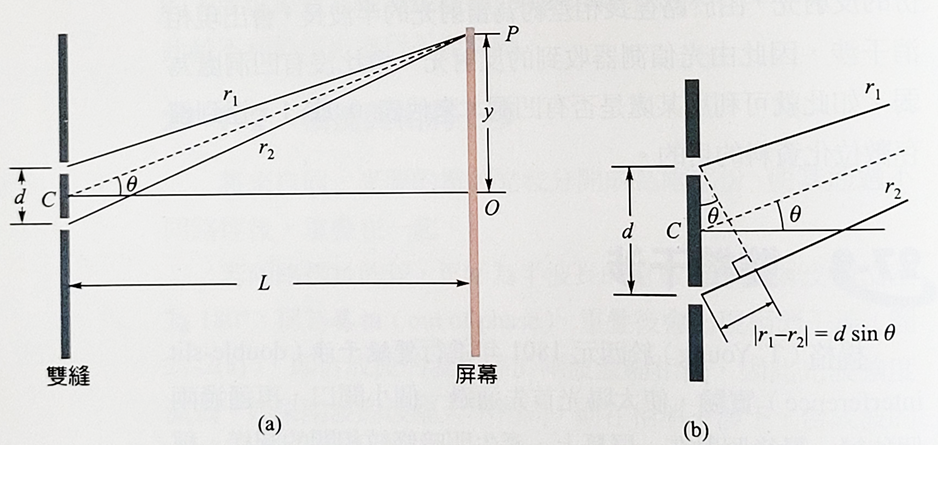
當光程差長\(|r_1-r_2|\)為半波長\(\lambda/2\)的奇數倍時,在\(P\)點會出現相消干涉,形成暗紋 \[ |r_1 - r_2| \simeq d \sin \theta = (m+\dfrac{1}{2}) \lambda ; \quad m \ge 0.\] 因\(\theta\)是小角度, \[d \sin \theta \simeq d \tan \theta = d \dfrac{y}{L}\] 我們可以利用這個近似公式將\(m\)級亮紋或暗紋與中央亮紋\(m=0\)之間隔\(y_m\)分別表示如下: \[y_m = m \lambda \dfrac{L}{d} \quad 亮紋\] \[y_m = (m + \dfrac{1}{2}) \lambda \dfrac{L}{d} \quad 亮紋\] 所以得到相鄰兩亮紋或兩暗紋之間的間隔可以近似為 \[\Delta y = y_m - y_{m-1} = \dfrac{L \lambda}{d} \] 上式顯示由干涉條紋之間隔可測出光波的波長。應用於測量光波的波長,這是雙狹縫干涉的一個很好應用。
光強度的分佈
接下來我們來探討經過雙狹縫干涉後光強度的分佈問題 從上面推導的公式只能得到干涉圖樣中光波強度的極大值和極小值究竟出現在屏幕上的什麼位置但無法得知光強度水位置連續變化的詳細情形 下面我們將要考慮光波的電場根據波的疊加原理可以求得光波強度在屏幕上的分佈情形 在上面所顯示的雙狹縫干涉實驗圖當中,由兩個狹縫出發到達屏幕上\(P\)點的光波,其電場在\(P\)點隨時間體的變化可表示為 \[E_1=E_{1P} \sin \omega t \quad E_2=E_{2P} \sin (\omega t + \phi) \] 其中\(E_{1P},\, E_{2P}\)是電場的振幅,\(\omega\)為波的角頻率,\(\phi\)為兩波因路程差\(|r_1 - r_2|\)而出現的相位差。當路程差 \[|r_1 - r_2|=d \sin \theta \ll L, \, r_1, \, r_2\] 時,兩個光波在\(P\)點的振幅可視為相等,也就是\(E_{1P}=E_{2P}=E_P\)。此外,由於光程差每增減一個波長時,相位差就增減\(2\pi\),所以可得 \[\dfrac{\phi}{2 \pi}=\dfrac{|r_1 - r_2|}{\lambda}=\dfrac{d \sin \theta}{\lambda} \] 依據線性疊加原理,合成波在\(P\)點的電場為 \[E=E_1 + E_2=2E_p \sin (\omega t + \dfrac{\phi}{2}) \cos(\dfrac{\phi}{2}) \]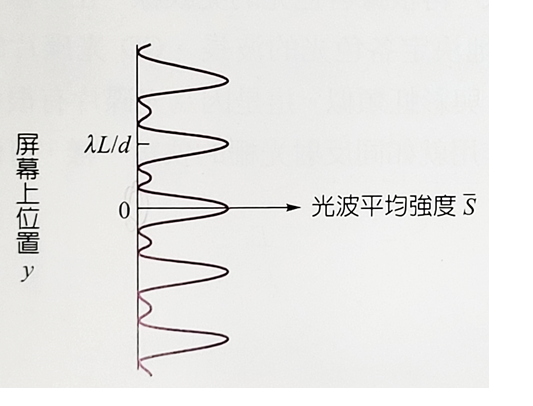 所以合成波的光波平均強度為
\[\bar{S}=\dfrac{[2 E_P \cos(\dfrac{\phi}{2})]^2}{2 \mu_0 c}=4\bar{S}_0 \cos^2 (\dfrac{\pi d \sin \theta}{\lambda}) \]
其中\(\bar{S}_0=\dfrac{E_P^2}{2 \mu_0 c}\)為每一光波的平均強度。公式中顯示了\(\bar{S}\)隨角度\(\theta\)而改變,其最大值為\(4\bar{S}_0\),最小值為0,分別出現在使右邊的餘弦為\(\pm 1\)和0的角度:
\[\dfrac{d \sin \theta}{\lambda}=m \,\, 與 \dfrac{d \sin \theta}{\lambda}=m+\dfrac{1}{2}. \]
這個結果和我們上面得到的公式顯然完全一樣。利用
\(d \sin \theta \simeq \dfrac{y}{L}\)
我們可以將上面的公式\(\bar{S}\)表示為P到點O距離\(y\)的函數,就可以得到右圖所顯示的干涉圖樣強度隨位置\(y\)的分佈。
所以合成波的光波平均強度為
\[\bar{S}=\dfrac{[2 E_P \cos(\dfrac{\phi}{2})]^2}{2 \mu_0 c}=4\bar{S}_0 \cos^2 (\dfrac{\pi d \sin \theta}{\lambda}) \]
其中\(\bar{S}_0=\dfrac{E_P^2}{2 \mu_0 c}\)為每一光波的平均強度。公式中顯示了\(\bar{S}\)隨角度\(\theta\)而改變,其最大值為\(4\bar{S}_0\),最小值為0,分別出現在使右邊的餘弦為\(\pm 1\)和0的角度:
\[\dfrac{d \sin \theta}{\lambda}=m \,\, 與 \dfrac{d \sin \theta}{\lambda}=m+\dfrac{1}{2}. \]
這個結果和我們上面得到的公式顯然完全一樣。利用
\(d \sin \theta \simeq \dfrac{y}{L}\)
我們可以將上面的公式\(\bar{S}\)表示為P到點O距離\(y\)的函數,就可以得到右圖所顯示的干涉圖樣強度隨位置\(y\)的分佈。
繞射光柵
狹縫很多而且間隔很小的多狹縫光柵也稱為繞射光柵,在光譜分析上非常有用。一般的繞射光柵橫寬僅約數公分,但每公分的狹縫數目則高達數千條。習慣上一條狹縫也稱為一條線,因此狹縫的間隔經常以每公分有多少條線表示。以上所討論的光柵產生干涉的光波,必須穿過個狹縫,因此稱為透射光柵。但有些光柵則是將入射的光波反生反射,以產生干涉,故稱所以稱為反射光柵。如\(\dfrac{d \sin \theta}{\lambda}=m\)所顯示的,干涉的級別\(m \ne 0\)的干涉亮紋的位置與波長有關,因此繞射光柵可取代三稜鏡分光計,可使入射光所含的各種色光分散開來,再根據各色光的亮紋在屏幕上出現的位置,就可精確的決定各色光的波長。CD光碟片的反光長具有多種顏色與彩虹類似,這是因為光碟片有很多條具有凹洞的圓軌,其作用就如同反射光柵的狹縫一樣,可使不同的色光分開。薄膜干涉
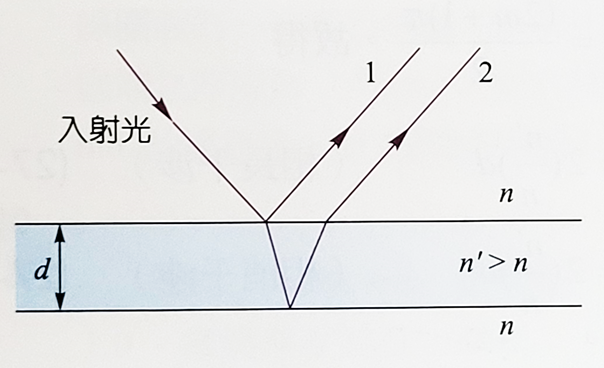 如圖所示當光照射到一個透明的薄膜時,在薄膜的上表面會有一部分被反射,而成為光線1,另有一部分則折射進入薄膜,而在下表面產生部分反射並回到上表面產生部分反射,在回到原介質中而成為光線2。由於光線1與2均源自於同一入射光,故具有相干性,可以產生穩定的干涉圖樣。假設薄膜的折射率\(n'\)大於周圍介質的折射率\(n\),則入射光波是以較快的波速入射到波速較慢的薄膜,因此其反射波會與入射波反相,這與弦波的情形一樣,就是當波由現質量密度較小的弦線進入密度較大的弦線時,反射波會與入射波反相位。反之,當弦波由波速較慢的介質進入波速較快的介質時,反射波會與入射波同相位。請注意無論是力學波或光波,折射或透射的波與入射波同相,而與進入的介質波速變快或變慢無關。
如圖所示當光照射到一個透明的薄膜時,在薄膜的上表面會有一部分被反射,而成為光線1,另有一部分則折射進入薄膜,而在下表面產生部分反射並回到上表面產生部分反射,在回到原介質中而成為光線2。由於光線1與2均源自於同一入射光,故具有相干性,可以產生穩定的干涉圖樣。假設薄膜的折射率\(n'\)大於周圍介質的折射率\(n\),則入射光波是以較快的波速入射到波速較慢的薄膜,因此其反射波會與入射波反相,這與弦波的情形一樣,就是當波由現質量密度較小的弦線進入密度較大的弦線時,反射波會與入射波反相位。反之,當弦波由波速較慢的介質進入波速較快的介質時,反射波會與入射波同相位。請注意無論是力學波或光波,折射或透射的波與入射波同相,而與進入的介質波速變快或變慢無關。設薄膜厚度為\(d\),入射光垂直入射薄膜表面,波長為\(\lambda\),則反射光線1,2的光程差\(L=2d\)。光波在薄膜內的波長是\(\lambda'=(\dfrac{n}{n'}) \lambda\),所以光線1與光線2由於在薄膜內之光程差會有相位差\(\Delta \phi=\dfrac{2 \pi L}{\lambda'}=\dfrac{4 \pi n' d}{n \lambda} \)。但當\(n' \gt n\)時,光線1在薄膜的上表面反射時,其相位與入射波反相,而光線2在薄膜的下表面反射,或在上表面折射時都沒有發生相位變化,所以反射光線1與2的相位差總共是 \[\Delta \phi=\Delta \phi' - \pi =\dfrac{2 \pi n' d}{n \lambda} - \pi\] 如果\(n' \lt n\),則僅有光線2在薄膜的下表面反射時發生反相,所以兩反射光線的相位差,仍然維持是\(\Delta \phi=\dfrac{2 \pi n' d}{n \lambda} - \pi\),這兩種情況所產生的相位差都是滿足相同的公式。由於反射光線1和2產生相相長干涉與相消干涉的條件分別為\(\Delta \pji= 2 m \pi \, 與 \, \dfrac{(2m +1) \pi}{2} \) \[(m+1/2)\lambda=2(n'/n)d \quad 相長干涉\] \[m \lambda=2(n'/n)d \quad 相消干涉\] 兩個公式中的整數\(=0,1,2,3...\)。
以上所得之干涉條件,只要薄膜上下方介質的折射率均大於或均小於薄膜的折射率,就可以適用。但若薄膜的折射率介於上下方介質折射率之間,則光波在上下表面的反射所產生的相位差相同,在此情況下上面兩個公式的相長干涉與相消干涉的條件,正好對調。因此如果在玻璃透鏡的鏡面上均勻地塗上和鍍上一層折射率\(n'\)介於空氣與玻璃之間的薄膜,並且薄膜的厚度正好滿足\((m+1/2)\lambda=2(n'/n)d \quad 相消干涉\),那麼經由薄膜上下表面反射的光,會產生相消干涉,而沒有反射光,也就是入射光會全部進入透鏡。此種抗反射敷層(anti-reflection coating)的厚度,其最小值\(d\)須能產生\(m=0\)的干涉,也就是 \[d=\dfrac{n \lambda}{4 n'}=\dfrac{\lambda}{4 n'}。\] 當入射光為單色光時,當薄膜的厚度隨位置而變,則有可能在若干個位置上,分別滿足 \[(m+1/2)\lambda=2(n'/n)d \quad 相長干涉\] \[m \lambda=2(n'/n)d \quad 相消干涉\] 在此情況下薄膜上將出現隨位置而變的干涉圖樣,亮紋與暗紋交替出現。當入射光是由多種波長不同的光波組成時,個別色光出現相長干涉與相消干涉的位置彼此不同,因此亮紋的顏色隨位置而變,形成多彩的干涉圖樣。這就是為什麼在陽光下的肥皂泡或油膜看來會有相間的各種彩色亮紋。
HL35示例問題-1
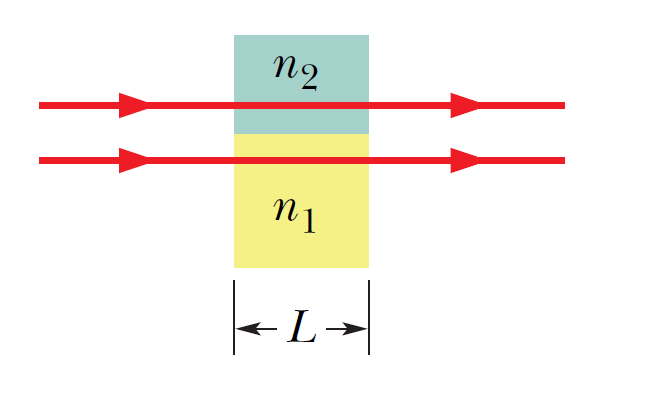 In the figure on the right, the two light waves that are represented by the rays have wavelength 550.0 nm before entering media 1 and 2. They also have equal amplitudes and are in phase. Medium 1 is just air, and medium 2 is a transparent plastic layer of index of refraction 1.6 and thickness 2.6 \(\mu\)m. (a) What is the phase difference of the emerging waves in wavelengths, radians, and degrees? What is their effective phase difference (in wavelengths)? (b) If the waves reached the same point on a distant screen, what type of interference would they produce?
In the figure on the right, the two light waves that are represented by the rays have wavelength 550.0 nm before entering media 1 and 2. They also have equal amplitudes and are in phase. Medium 1 is just air, and medium 2 is a transparent plastic layer of index of refraction 1.6 and thickness 2.6 \(\mu\)m. (a) What is the phase difference of the emerging waves in wavelengths, radians, and degrees? What is their effective phase difference (in wavelengths)? (b) If the waves reached the same point on a distant screen, what type of interference would they produce?在右圖中,由射線表示的兩個光波在進入介質 1 和 2 之前的波長為 550.0 nm。它們也具有相等的幅度並且同相。 介質 1 只是空氣,介質 2 是折射率為 1.6、厚度為 2.6 \(\mu\)m 的透明塑料層。 (a) 新出現的波在波長、弧度和度數方面的相位差是多少? 它們的有效相位差(波長)是多少? (b) 如果波到達遠處屏幕上的同一點,它們會產生什麼類型的干擾?
(a)
\[ \begin{equation} \begin{split} N_2-N_1 &=\dfrac{L}{\lambda}(n_2-n_1) \\ &=\dfrac{2.6 \times 10^{-6}}{5.5 \times 10^{-7}}(1.6-1.0) &=2.84 \end{split} \end{equation} \] (b) \(\text{phase difference}=2.84 \lambda =2.84 (2\pi) \, \text{rad} \simeq 1020^{\circ}\)
\(\text{effective phase difference}=0.84 \lambda\)
HL35示例問題-2
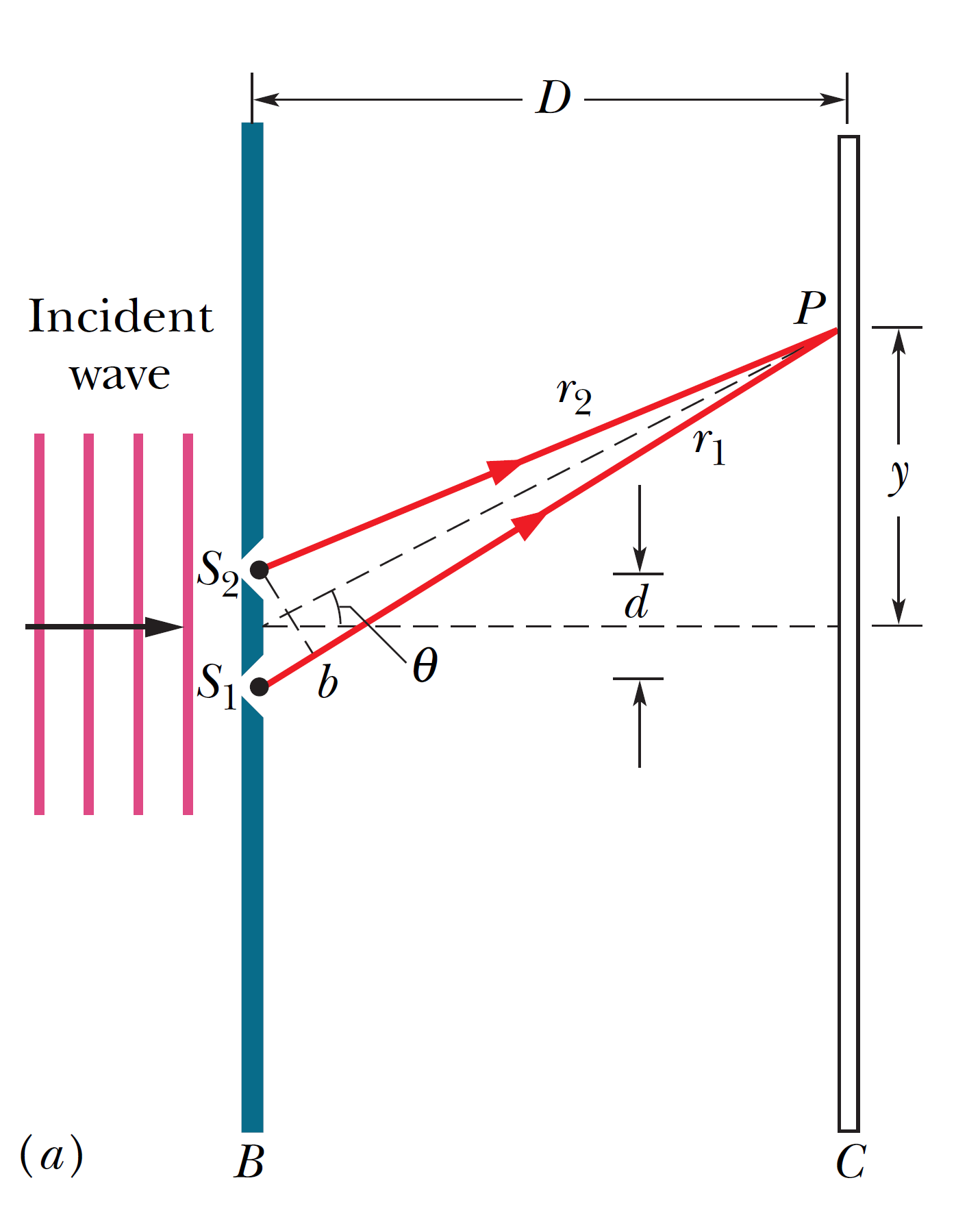 What is the distance on screen \(C\) in the figure between adjacent maxima near the center of the interference pattern? The wavelength \(\lambda\) of the light is 546 nm, the slit separation \(d\) is 0.12 mm, and the slit–screen separation \(D\) is 55 cm. Assume that \(\theta\) is small enough to permit use of the approximations \(\sin \theta \simeq \tan \theta \simeq \theta\), in which \(\theta\) is expressed in radian.
What is the distance on screen \(C\) in the figure between adjacent maxima near the center of the interference pattern? The wavelength \(\lambda\) of the light is 546 nm, the slit separation \(d\) is 0.12 mm, and the slit–screen separation \(D\) is 55 cm. Assume that \(\theta\) is small enough to permit use of the approximations \(\sin \theta \simeq \tan \theta \simeq \theta\), in which \(\theta\) is expressed in radian. 圖中屏幕\(C\)上乾涉圖案中心附近相鄰最大值之間的距離是多少? 光的波長 \(\lambda\) 為 546 nm,狹縫間距 \(d\) 為 0.12 mm,狹縫-屏幕間距 \(D\) 為 55 cm。 假設 \(\theta\) 小到足以允許使用近似值 \(\sin \theta \simeq \tan \theta \simeq \theta\),其中 \(\theta\) 以弧度表示。
\(\tan \theta \simeq \theta = \dfrac{y_m}{D}\)
Consider the angle \(\theta\) for the m-th maximum,
\(d\sin\theta=m\lambda; \Rightarrow \sin \theta \simeq \theta = \dfrac{m \lambda}{d}\)
\(y_m=\dfrac{m \lambda D}{d}\)
For (m+1)-th maximum,
\(y_{m+1}=\dfrac{(m+1) \lambda D}{d}\)
\[ \begin{equation} \begin{split} \Delta y &=y_{m+1}-y_m = \dfrac{\lambda D}{d} \\ &=\dfrac{(546 \times 10^{-9})(55 \times 10^{-2})}{0.12 \times 10^{-3}}(1.6-1.0) &=2.50 \times 19^{-3} \text{m} \end{split} \end{equation} \]
HL35示例問題-3
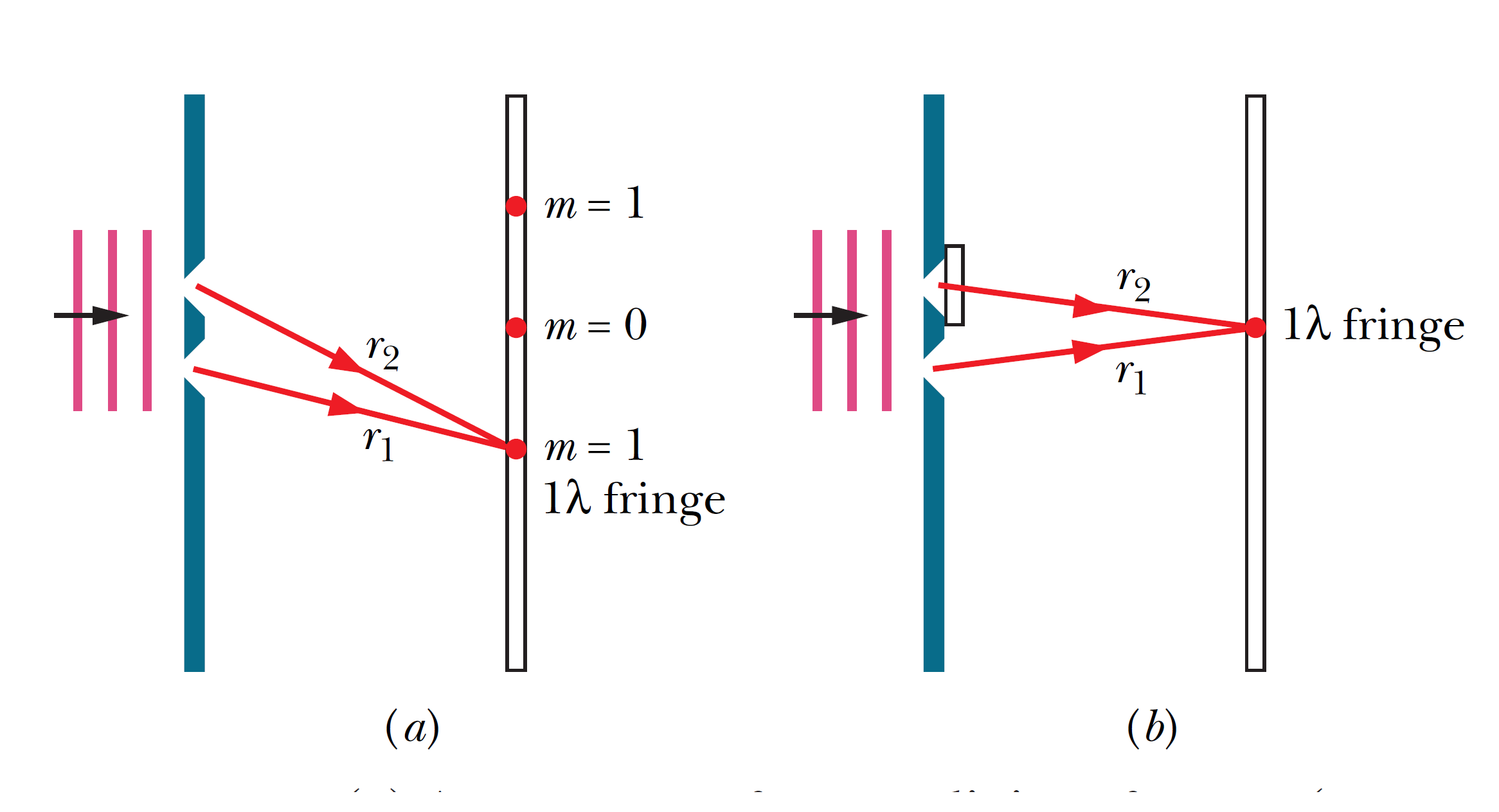 A double-slit interference pattern is produced on a screen, as in the figure; the light is monochromatic at a wavelength of 600 nm. A strip of transparent plastic with index of refraction \(n = 1.50\) is to be placed over one of the slits. Its presence changes the interference between light waves from the two slits, causing the interference pattern to be shifted across the screen from the original pattern. Figure (a) shows the original locations of the central bright fringe (\(m = 0\)) and the first bright fringes (\(m = 1\)) above and below the central fringe. The purpose of the plastic is to shift the pattern upward so that the lower (\(m = 1\)) bright fringe is shifted to the center of the pattern. Should the plastic be placed over the top slit (as arbitrarily drawn in figure (b)) or the bottom slit, and what thickness \(L\) should it have?
A double-slit interference pattern is produced on a screen, as in the figure; the light is monochromatic at a wavelength of 600 nm. A strip of transparent plastic with index of refraction \(n = 1.50\) is to be placed over one of the slits. Its presence changes the interference between light waves from the two slits, causing the interference pattern to be shifted across the screen from the original pattern. Figure (a) shows the original locations of the central bright fringe (\(m = 0\)) and the first bright fringes (\(m = 1\)) above and below the central fringe. The purpose of the plastic is to shift the pattern upward so that the lower (\(m = 1\)) bright fringe is shifted to the center of the pattern. Should the plastic be placed over the top slit (as arbitrarily drawn in figure (b)) or the bottom slit, and what thickness \(L\) should it have?如圖所示,在屏幕上產生雙縫干涉圖案; 光是波長為 600 nm 的單色光。 一條折射率為 \(n = 1.50\) 的透明塑料條將放置在其中一個狹縫上。 它的存在改變了來自兩個狹縫的光波之間的干涉,導致干涉圖案從原始圖案在屏幕上移動。 圖 (a) 顯示了中心亮條紋 (\(m = 0\)) 和中心條紋上方和下方的第一條亮條紋 (\(m = 1\)) 的原始位置。 塑料的目的是使圖案向上移動,使較低的 (\(m = 1\)) 亮條紋移動到圖案的中心。 塑料應該放在頂部狹縫(如圖(b)中任意繪製)還是底部狹縫上,它應該有什麼厚度\(L\)?
HL35示例問題-4
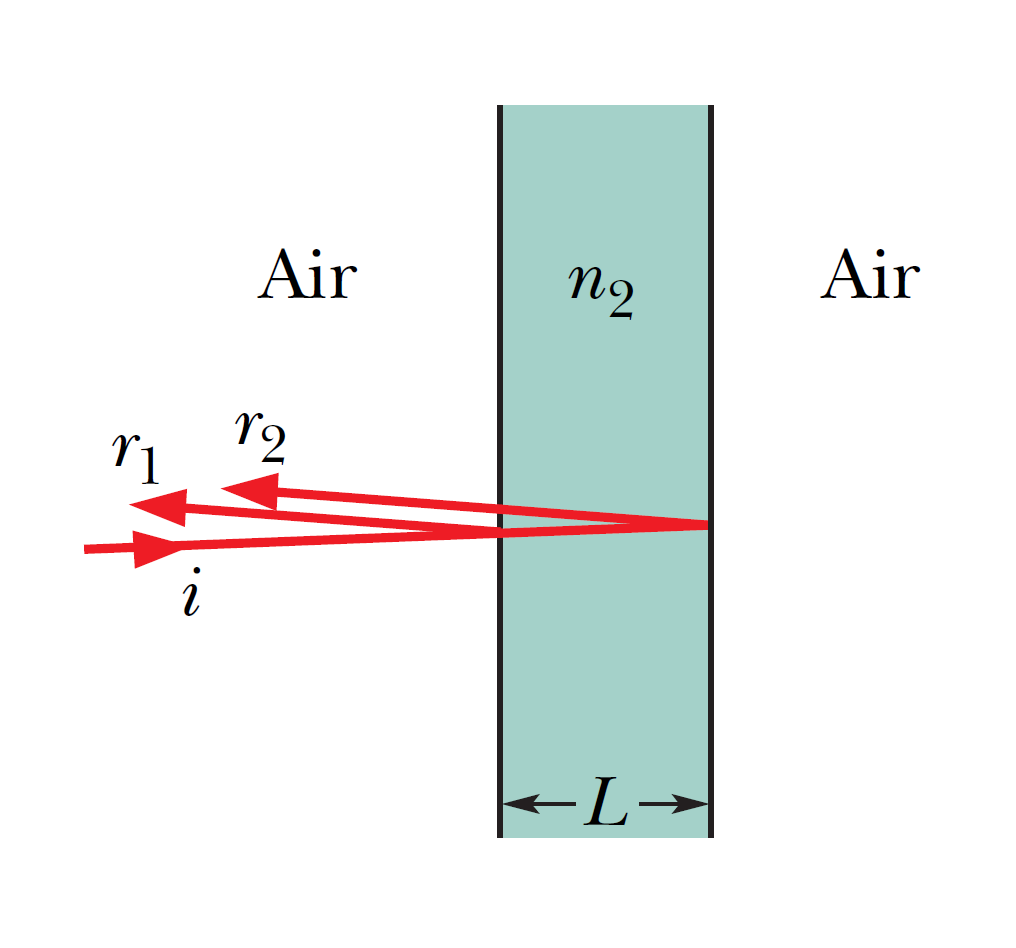 White light, with a uniform intensity across the visible wavelength range of 400 to 690 nm, is perpendicularly incident on a water film, of index of refraction \(n_2 = 1.33\) and thickness \(L = 320\) nm, that is suspended in air. At what wavelength \(\lambda\) is the light reflected by the film brightest to an observer?
White light, with a uniform intensity across the visible wavelength range of 400 to 690 nm, is perpendicularly incident on a water film, of index of refraction \(n_2 = 1.33\) and thickness \(L = 320\) nm, that is suspended in air. At what wavelength \(\lambda\) is the light reflected by the film brightest to an observer?白光在 400 到 690 nm 的可見波長范圍內具有均勻的強度,垂直入射在折射率為 \(n_2 = 1.33\) 和厚度 \(L = 320\) nm 的水膜上,即 懸浮在空氣中。 在什麼波長 \(\lambda\) 處,薄膜反射的光對觀察者來說最亮?
\[2L=\dfrac{\text{odd number}}{2} \times \dfrac{\lambda}{n_2}\] \[2L=(m+1/2)\dfrac{\lambda}{n_2}\] \[\lambda=\dfrac{2 n_2 L}{m+ \frac{1}{2}}=\dfrac{851\, \text{nm}}{m+\frac{1}{2}}\] \[\text{for m=0:} \quad \lambda=1700 \, \text{nm} \quad \text{infrared}\] \[\text{for m=1:} \quad \lambda=576 \, \text{nm} \quad \text{yellow green}\] \[\text{for m=2:} \quad \lambda=340 \, \text{nm} \quad \text{ultraviolet}\]
HL35示例問題-5
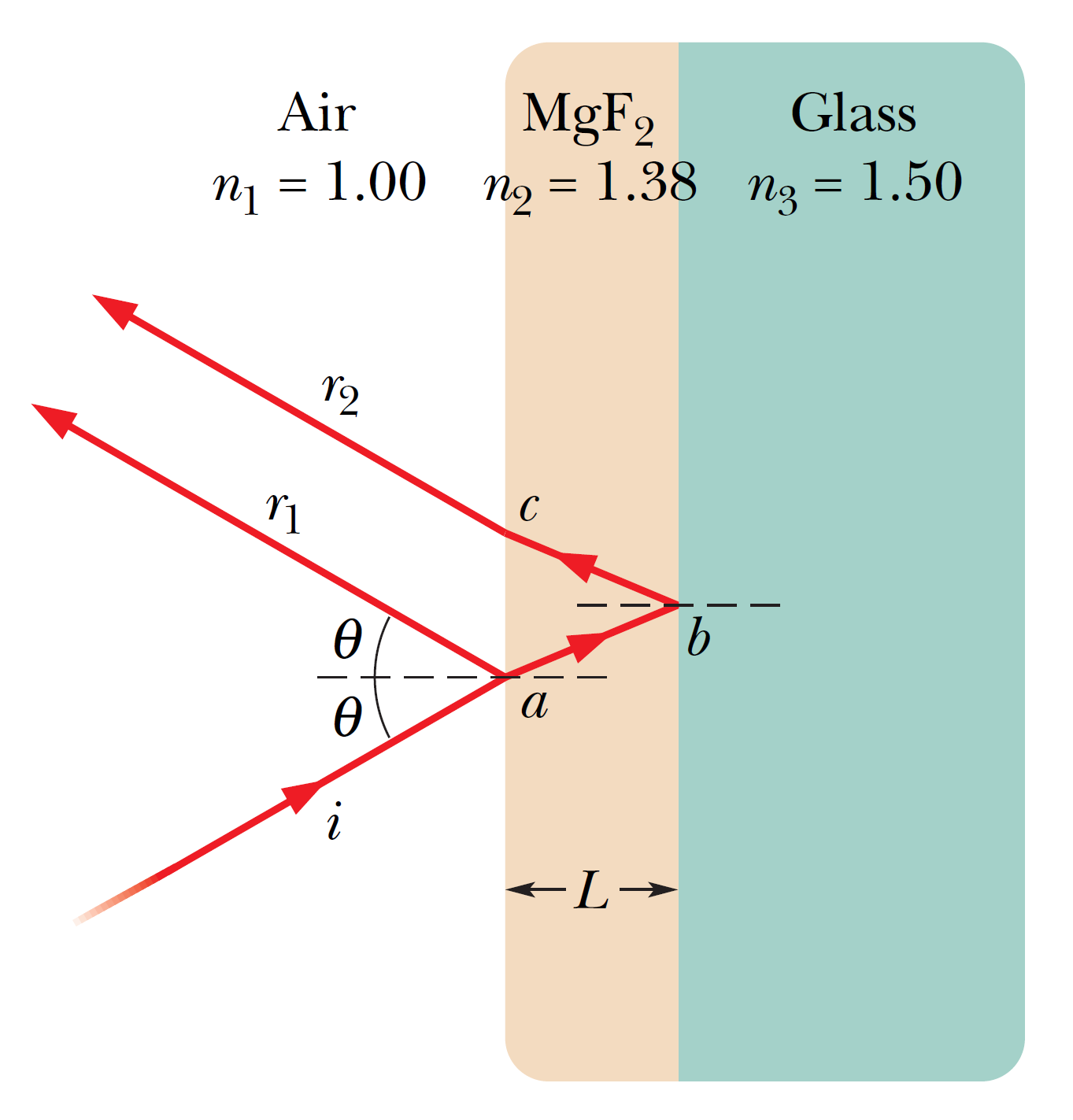 In the figure, a glass lens is coated on one side with a thin film of magnesium fluoride (MgF2) to reduce reflection from the lens surface.The index of refraction of MgF2 is 1.38; that of the glass is 1.50.What is the least coating thickness that eliminates (via interference) the reflections at the middle of the visible spectrum (\(\lambda=550 \, \text{nm}\))? Assume that the light is approximately perpendicular to the lens surface.
In the figure, a glass lens is coated on one side with a thin film of magnesium fluoride (MgF2) to reduce reflection from the lens surface.The index of refraction of MgF2 is 1.38; that of the glass is 1.50.What is the least coating thickness that eliminates (via interference) the reflections at the middle of the visible spectrum (\(\lambda=550 \, \text{nm}\))? Assume that the light is approximately perpendicular to the lens surface. 圖中,玻璃鏡片的一側塗有一層氟化鎂薄膜(MgF2),以減少鏡片表面的反射。MgF2的折射率 子> 是 1.38; 玻璃的厚度是 1.50。消除(通過干涉)可見光譜中間反射的最小塗層厚度是多少(\(\lambda=550\,\text{nm}\))? 假設光線大致垂直於透鏡表面。
在第一個界面,入射光在空氣中,空氣的折射率低於 MgF2(薄膜)。因此,我們將在 \(r_1\) 下有 0.5 個波長;射線波 \(r_1\) 在第一個界面處移動了 0.5 \(\lambda\)。在第二個界面,入射光在 MgF2 中,它的折射率比界面另一側的玻璃小。因此,我們將在 \(r_2\) 下有 0.5 個波長。因為兩種反射都會導致相同的相移,所以它們傾向於使 \(r_1\) 和 \(r_2\) 的波同相。由於我們希望這些波是異相的,因此它們的路徑長度差 2L 必須是奇數個半波長: \[2L=\dfrac{\text{odd number}}{2} \times \dfrac{\lambda}{n_2}\] 我們希望塗層的厚度最小,即 \(L\) 的最小值。因此,我們選擇 \(m = 0\),這是 \(m\) 的最小可能值。代入它和給定的數據,我們得到 \[L=\dfrac{\lambda}{4 n_2}=\dfrac{550}{(4)(1.38)}=99.6 \, \text{nm} \]
陳永忠 email:ycchen@thu.edu.tw