波動光學2-繞射
研究光的物理學的一個重點是理解和利用光在穿過狹窄狹縫或（我們將討論）穿過狹窄障礙物或邊緣時的衍射。我們在第 1 章中談到了這一現象 35 當我們看到光是如何通過 Young 實驗中的狹縫發生耀斑（衍射）時的。 然而，通過給定狹縫的衍射比簡單的閃光更複雜，因為光也會干擾自身並產生干涉圖案。 正是因為這樣的複雜性，光才擁有豐富的應用機會。 儘管光通過狹縫或障礙物時的衍射看起來非常學術，但無數工程師和科學家以這種物理學為生，全球衍射應用的總價值可能無法估量。 在我們討論其中一些應用之前，我們首先必須討論為什麼衍射是由於光的波動性。海更士原理
波的基本特性之一就是能夠干涉，而另一個特性就是繞射，也就是能繞過障礙物轉彎前進的特性。繞射與干涉的關係密切，以上討論過的雙狹縫和多狹縫光柵，其干涉現象其實也與繞射有關，因此才有繞射光柵的稱呼。海更士提倡光是一種波動，並且於1678年提出海更士原理，說明光和其他波動的繞射現象。這個原理與馬克斯威爾電磁理論的推論一致，但比較簡單而且易於應用，其內容大略如下：
在一個波前上的各點，都可當作點波源，發出子波，子波為球面波，以介質中之波速傳遞，在某一瞬間時，與所有向前傳播的子波球面相切的面，就是新的波前。
繞射
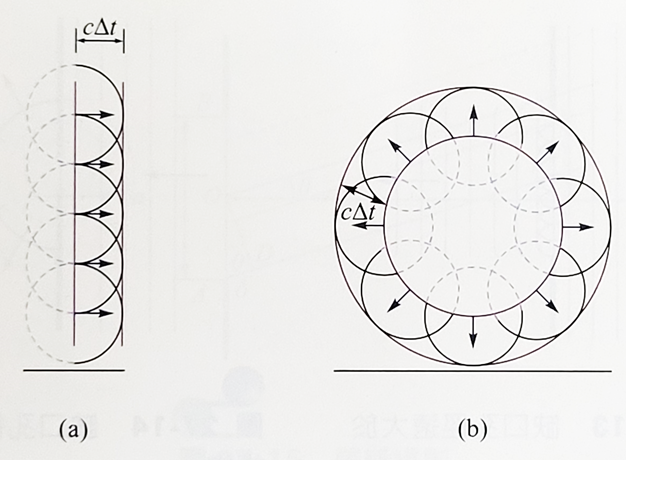
當一個平面波沿一直線前進到一個障礙物的缺口時，依據海更士原理在缺口的波前發出球面子波，形成新的波前繼續前進。如果缺口孔徑遠較波長為大，則如圖所示新的波前基本上還是平面，進入缺口的能量幾乎全部沿著原來入射的方向前進，繞射現象並不顯著。但是如果缺口的孔徑與波長相當，如圖所示新的波前將接近球面，波的前進方向就分散開來，與原來入射的方向不同，明顯出現轉彎繞射的現象。在幾何光學中通常都假設光的波長遠小於考慮的缺口或障礙物的尺寸，因此就像圖左的情形可忽略繞射，而將光當作直線前進。但要是微小的物體成像於光學系統中或使光束精確的聚焦時，繞射的影響就不能被忽視而無法避免。
單狹縫繞射
以上在討論雙狹縫和多狹縫干涉現象時，都假設每一道狹縫的寬度，遠比入射光的波長為短而可忽略。因此依據海更斯原理，當入射光到達個狹縫時，每一條狹縫都有如上圖左所顯示，可以當作一個線光源發出球面波，延不同方向前進至屏幕上各部分，並且與其他狹縫發出的球面波產生干涉，形成干涉圖樣。但是如果一個單獨的狹縫其寬度與入射光的波長相差不多，無法加以忽略，則根據海更斯原理狹縫的各部分都可視為線光源，各自發出球面波，彼此干涉。這種寬度與波長相當的狹縫，實際上就像是具有無窮多個狹縫的多縫光柵可以在屏幕上形成干涉圖樣，稱為繞射圖樣(diffraction pattern)。這種單狹縫的干涉現象，稱為單縫繞射。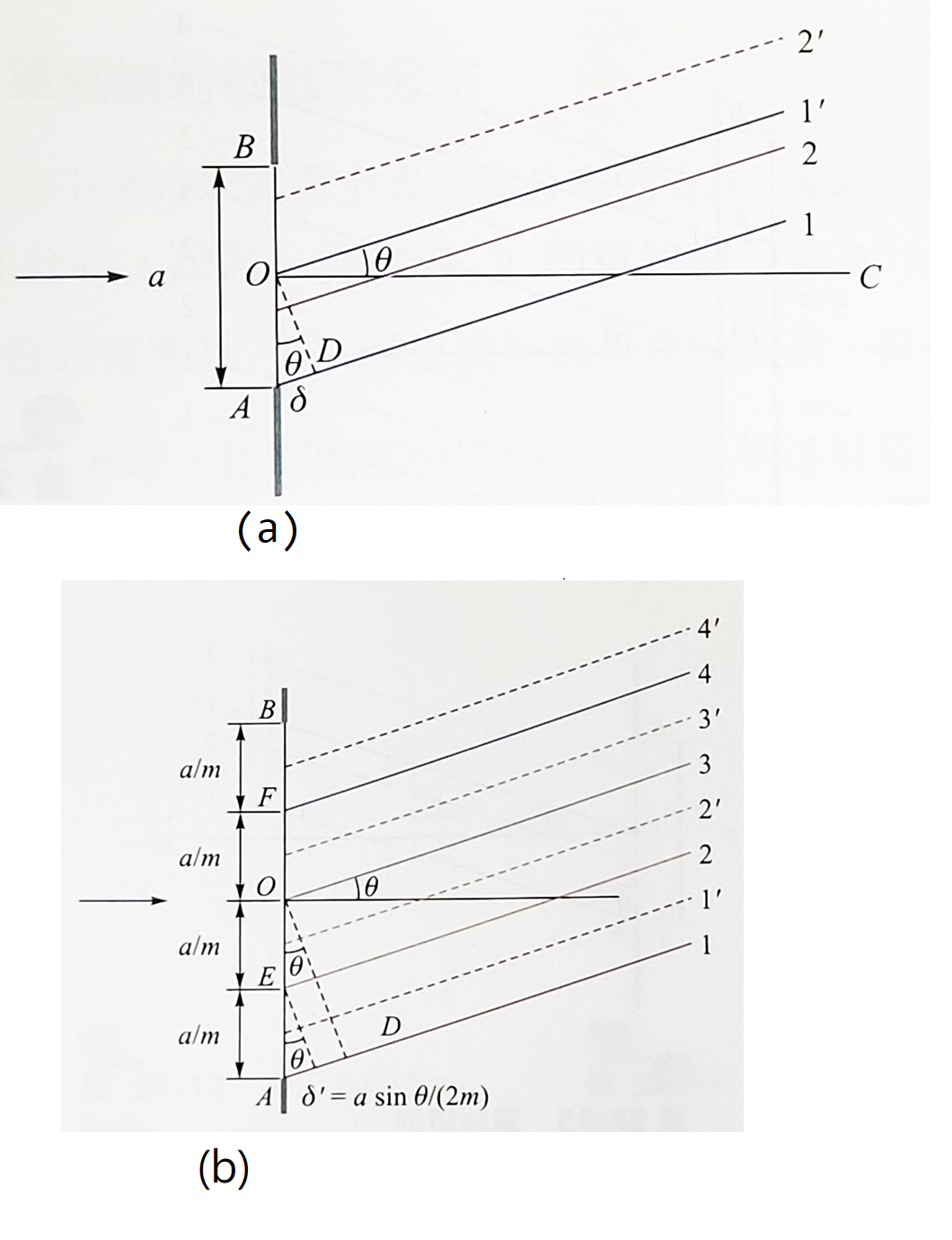
如右圖(a)所示假設平面波沿\(OC\)方向入射到一個寬度為\(a\)的單狹縫，則依據海更斯原理，在狹縫\(AB\)上的各點均可當作光源，發出球面子波朝右邊各個方向前進。若屏幕與狹縫的距離遠大於縫寬，\(L \gg a\)，則到達屏幕上同一點\(P\)的各個子波，其路線可視為彼此平行，且與光波入射方向的夾角均為\(\theta\)。假設\(O\)為狹縫的等分點，則光線1與1'的光程差為\(\delta=\overline{AD}=\dfrac{a \sin \theta}{2}\)。狹縫上半段\(OB\)中任一位置發出的光線，與以下半段\(AO\)中位於其下\(\dfrac{a}{2}\)的位置所發出的光線，例如圖中的2與2'光線，也都具有相同的光程差\(\delta\)。所以當光程差隨\(\theta\)角增加而達半波長\(\dfrac{\lambda}{2}\)時，
\[\delta=\dfrac{a}{2} \sin \theta = \dfrac{\lambda}{2} \]
由狹縫各點發出的光線，將出現上半段與下半段成對相消的情形，因此在屏幕上的\(P\)點將出現相消干涉，形成暗紋。事實上當光程差等於半波長的整數倍時，亦即 \[\delta=\dfrac{a}{2} \sin \theta = m \dfrac{\lambda}{2} \] 可以設想狹縫被等分為\(m\)部分，如右圖(b)所示，每部分的寬度均為\(\dfrac{a}{m}\)。由上面的公式，在此種分割方法下，每部分的光程差正好為半波長 \[\delta'=\dfrac{\delta}{m}=\dfrac{a \sin \theta}{2 m}\] 所以每部分將如上述光程差\(\delta=\dfrac{\lambda}{2}\)的情況，出現光線成對相消的現象，因此在屏幕上的\(P\)點會出現相消干涉，形成暗紋。綜合以上的討論可以得到單狹縫繞射的條件： \[a \sin \theta = m \lambda, \quad m= 1,2,3,... \quad (相消干涉)\]
例題
平面光波入射到單狹縫後，中央亮紋兩側\(m=1\)繞射暗紋的夾角\(2 \theta\)可用以衡量光線散開的角度。假設一個單狹縫的寬度為入射光波長的10倍，則光線透過通過單狹縫後散開的角度為何？
設波長\(\lambda\)，縫寬為\(\alpha=10 \lambda\)，\(m=1\)， \[\sin \theta = \dfrac{m \lambda}{\alpha}=\dfrac{1}{10}\] \[2 \theta = 2 \sin^{-1} (0.1)=11.5^{\circ} \]
設波長\(\lambda\)，縫寬為\(\alpha=10 \lambda\)，\(m=1\)， \[\sin \theta = \dfrac{m \lambda}{\alpha}=\dfrac{1}{10}\] \[2 \theta = 2 \sin^{-1} (0.1)=11.5^{\circ} \]
單狹縫繞射的強度分佈
仿照雙狹縫干涉時求屏幕上光強度分佈的方法，可以計算單狹縫繞射的強度分佈。假設將一個寬度為\(a\)的單狹縫，等分為\(N\)個部分，則每部分的寬度為\(a/N\)。當以波長為\(\lambda\)的光照射，且子波光線的偏角為\(\theta\)時，相鄰兩部分所發出的光波到達屏幕上同一點\(P\)時，其光程差為\(\delta=\dfrac{a \sin \theta}{N}\)，電場的相位差為\(\phi=\dfrac{2 \pi \delta}{\lambda}\)，而狹縫上、下邊緣發出的光波其相位差為\(\P\)，也就是總相位差可表示為 \[ \Phi=N\phi=\dfrac{2\pi N \delta}{\lambda}=\dfrac{2\pi a \sin \theta}{\lambda}\]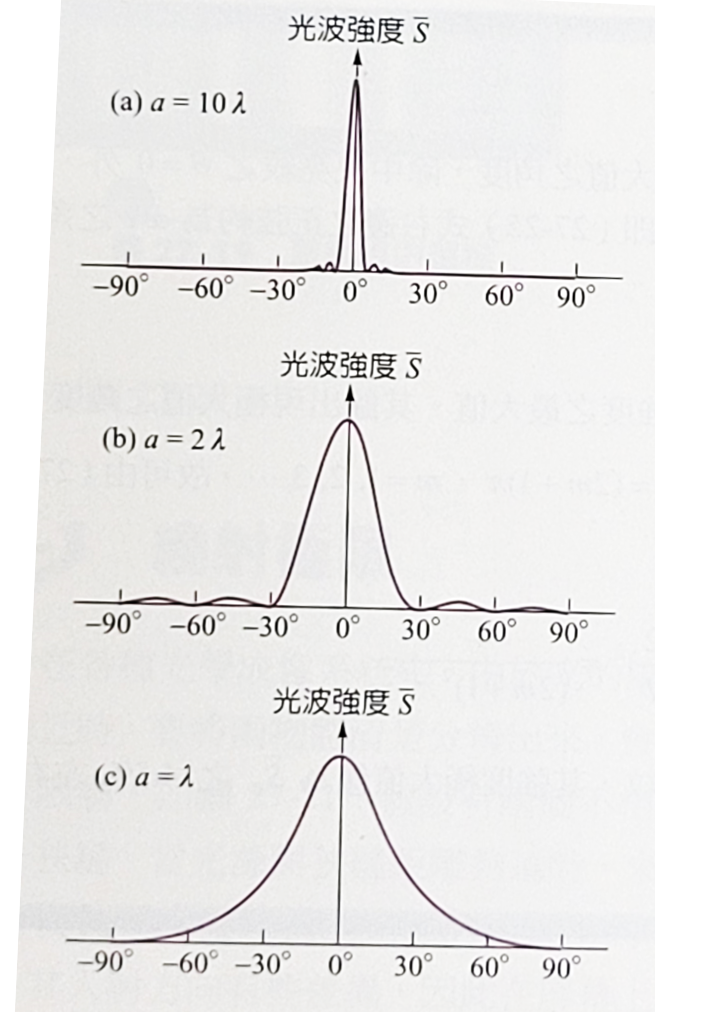
在屏幕上光的強度是電場的平方對時間的平均值，這些計算可以利用電場向量線性疊加的phasor方法來實現，細節我們在此不討論，其結果如下。光波在\(P\)點的電場隨角度與時間的函數： \[E(\theta, t)=E_0 \dfrac{\sin (\Phi/2)}{\Phi/2} \sin(\omega t + \Phi/2)，\quad \Phi= \dfrac{2\pi a \sin \theta}{\lambda}\] 將電場平方並且取時間的平均，可以得到光波的平均強度 \[\bar{S}=\bar{S}_0 \left( \dfrac{\Phi/2}{\Phi/2} \right)^2 \] \[\bar{S}_0=\dfrac{E_0^2}{2 \mu_0 c} \] 其中\(\bar{S}_0\)是角度\(\theta=0\)時的光波平均強度，並且\(\bar{S}\)隨角度改變時其最大值為出現在\(\theta=0\)處，最小值為0，出現在上面公式右邊正弦函數為0的地方\(\sin (\Phi/2)=0\)，也就是下面的條件 \[ a \sin \theta = m \lambda \quad m=1,2,3...\] 這個結果和使用光程差的討論所得到的結論完全一致。利用光波平均強度的公式，我們可以畫出繞射圖樣強度\(\bar{S}(\theta)\)隨角度\(\theta\)的分佈。在右圖當中我們分別畫出狹縫寬度分別是波長的10倍，2倍和1倍的情況下，光波在屏幕上的強度隨角度的變化函數圖形。我們可以明顯地看到，當俠縫的寬度很寬，是波長的10倍的時候，光波在屏幕上分佈的角度非常狹窄，幾乎全部都在0度附近，也就是光的行進沒有產生偏移繞射的現象，非常接近幾何光學所假設的直線行進的行為。隨著狹縫變窄，光波在屏幕上的分佈角(寬)度加大，當狹縫寬度是波長2倍的時候，光波的分佈角度在上下各30度，共\(60^{\circ}\)。而當狹縫寬度恰好就是光波的波長時，總共分佈的角度可以達到\(120^{\circ}\)。這就說明了光波的波動現象被偵測到的條件，就是狹縫或障礙物的尺度接近於光波的波長時，才容易出現，可被觀測。光波作為波動的特性在這個條件下(\(a \simeq \lambda\))才會彰顯出來。
例題
單狹縫繞射圖樣中光波強度出現極大值的角度，除中央亮紋的\(\theta =0 \)之外。其餘大約為在強度為零之兩暗紋中間，也就是公式中右邊的\(\sin\)為\(\pm 1\)的角度。請計算單狹縫繞射圖案中，各強度極大值的比值。
中央亮紋之強度為強度之最大，其餘出現極大值的角度\(\theta\)是\(\sin(\Phi/2) \simeq \pm 1\)，也就是\(\Phi \simeq (2m+1) \pi, \,\, m=1,2,3,... \)，將這些數值代進強度公式當中，可以得到對應於m的強度極大值為 \[\dfrac{\bar{S}_m}{\bar{S}_0}=\left( \dfrac{2}{\Phi} \right)^2 =\dfrac{4}{(2m+1)^2 \pi^2} \] 例如\(\dfrac{\bar{S}_1}{\bar{S}_0}=\dfrac{4}{9 \pi^2}=0.045\)，也就是\(m=1\)的亮紋其強度極大值僅為最大值的4.5%左右。
中央亮紋之強度為強度之最大，其餘出現極大值的角度\(\theta\)是\(\sin(\Phi/2) \simeq \pm 1\)，也就是\(\Phi \simeq (2m+1) \pi, \,\, m=1,2,3,... \)，將這些數值代進強度公式當中，可以得到對應於m的強度極大值為 \[\dfrac{\bar{S}_m}{\bar{S}_0}=\left( \dfrac{2}{\Phi} \right)^2 =\dfrac{4}{(2m+1)^2 \pi^2} \] 例如\(\dfrac{\bar{S}_1}{\bar{S}_0}=\dfrac{4}{9 \pi^2}=0.045\)，也就是\(m=1\)的亮紋其強度極大值僅為最大值的4.5%左右。
雙狹縫繞射
如果你讓光通過大量均勻分佈的平行狹縫，稱為衍射光柵，就會發生一件有趣的事情。創建的干涉圖案與雙縫形成的干涉圖案非常相似（見圖 27.16）。衍射光柵可以通過用鋒利的工具在許多精確定位的平行線上劃傷玻璃來製造，未觸及的區域就像狹縫一樣。這些可以相當便宜地以照相方式大量生產。衍射光柵既可用於透射光，如圖 27.16 所示，也可用於反射光，如圖 27.17 中的蝴蝶翅膀和澳大利亞蛋白石或本章開篇照片中所示的 CD，圖 27.1。除了用作新奇物品外，衍射光柵通常用於光譜色散和光分析。使它們特別有用的是它們形成比雙縫更清晰的圖案。也就是說，它們的亮區更窄更亮，而它們的暗區更暗。圖 27.18 顯示了展示更清晰模式的理想化圖表。自然衍射光柵出現在某些鳥類的羽毛中。規則圖案中的細小指狀結構充當反射光柵，產生相長干涉，使羽毛顏色不僅僅是因為它們的色素沉著。這稱為虹彩。
右圖 (a) 顯示了一個實際雙狹縫繞射相片，其中雙縫干涉和繞射都很明顯。
從繞射的強度分析中，我們已經知道，光波繞射的最大值和第二極大值之間的強度差異很大，因此在右圖(b)的繞射相片中，我們過度曝光，目的就在彰顯出次級最大值的所在位置。如果一個狹縫被覆蓋，則只產生圖 (b) 的單狹縫衍射圖案。注意上圖與右圖之間的對應關係。在上圖(c)與右圖(a)對應，以及上圖(b)與右圖(b)對應。利用電場的phaser計算、線性疊加原理以及光波強度與電場的關係，我們可以計算考慮雙狹縫在有線寬度下，繞射光波在屏幕上的平均強度隨角度的變化關係。具繞射效應的雙縫干涉的強度公式如下(我們略過這個公式的推導)：
\[I(\theta)=I_m (\cos^2 \beta) \left( \dfrac{\sin \alpha}{\alpha} \right)^2 \]
\[ \beta=\dfrac{\pi d}{\lambda} \sin \theta \]
\[ \alpha=\dfrac{\pi a}{\lambda} \sin \theta \]
其中 \(d\) 是狹縫中心之間的距離，\(a\) 是狹縫寬度，\(I_m\)是繞射平均強度的最大值。從公式中我們可以看到，光波的平均強度的分佈函數與狹縫之間的距離\(d\)和狹縫的寬度\(a\)有關。當狹縫的寬度\(a \ll d\)，光波的平均強度公式會變趨近於雙狹縫干涉的強度公式；相對的，如果狹縫非常寬\(d=0\)，以至於兩個狹縫變成單獨一個狹縫時，上面的公式又會退化為單狹縫繞射的強度公式。
繞射光柵
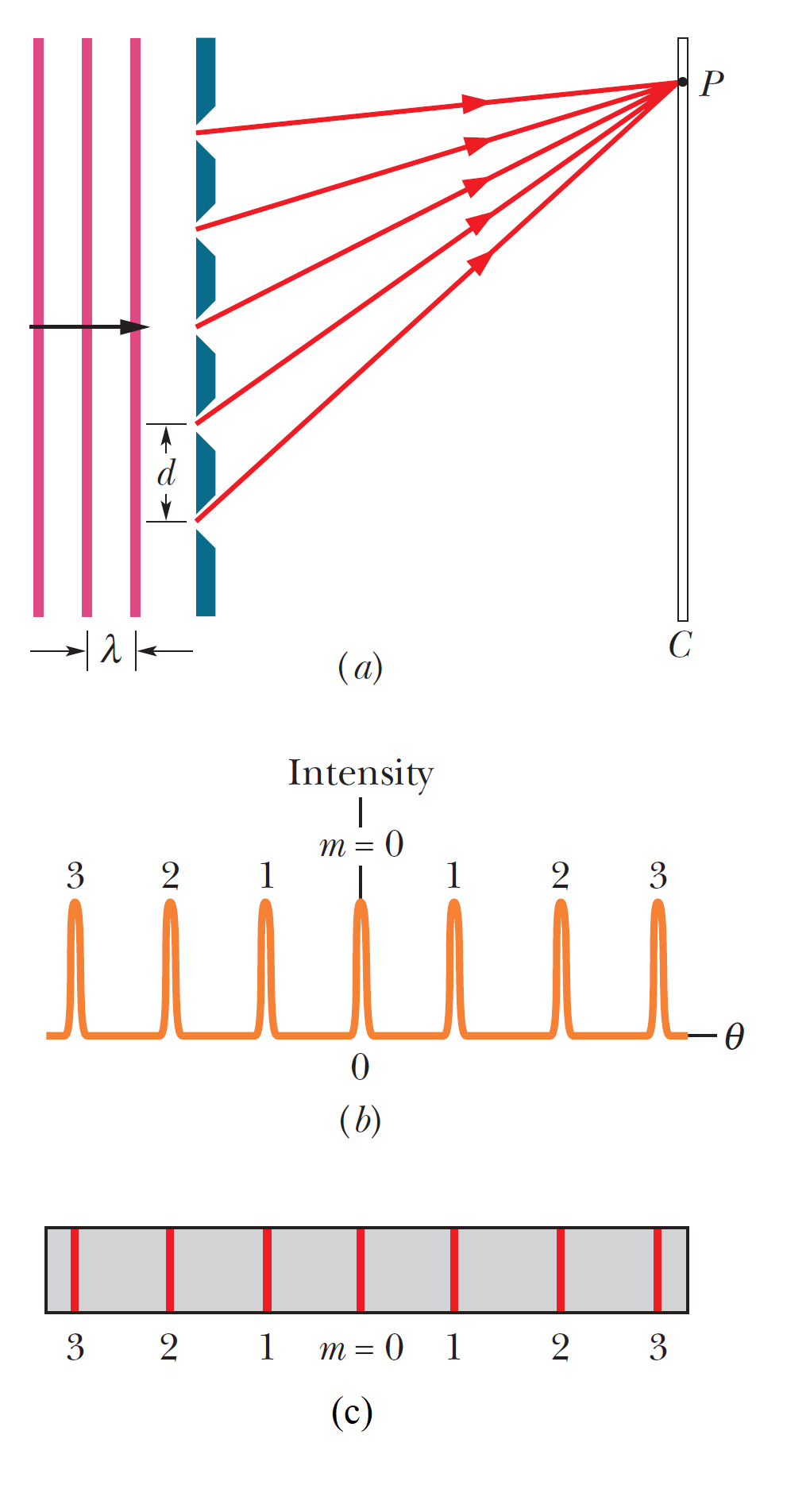在所有用光學原理與工具，來研究物體發光和吸收光的性質當中，繞射光柵是其中最有用的工具之一。繞射光柵的基本構造與雙狹縫干涉非常像，但是狹縫的數目N遠大於2，典型的光柵密度約為每毫米有數千條狹縫。在右圖中我們呈現一個理想的有5條狹縫的繞射光柵。當單色光照射在這些狹縫上，會在屏幕上產生非常狹窄的干涉條紋，利用測量這些狹窄的條紋的位置，可以幫助我們決定光的波長。繞射光柵也可以是不透明的表面，製作具有狹窄的平行凹槽的狹縫排列，然後光從凹槽反射回來，(而不是通過開口狹縫而透射)利用反射一樣可以達到光柵的作用，一樣會產生狹窄的干涉條紋。請注意，當單色光入射到繞射光柵時，如果我們逐漸將狹縫的數量從 2 增加到較大的 N，光波的強度圖會從典型的雙縫圖，變為更複雜的圖，然後最終變為像右圖所示，亮紋變得更為狹窄，能夠更精確測量出亮紋最中央的位置，進而能夠更精確的決定光的波長。使用來自例如氦-氖激光器的單色紅光，在觀察屏幕上看到的圖案相片如右圖所示。最大值非常窄，它們被相對較寬的暗區隔開。我們可以使用已經非常熟悉的光程差的分析方法來計算屏幕上亮線的位置。我們首先假設屏幕離光柵足夠遠，因此到達屏幕上特定點 \(P\) 的光線在離開光柵時大致平行。然後我們對每對相鄰的狹縫應用與雙縫干涉相同的光程差的計算，決定亮紋出現的條件如下：刻線之間的間隔 \(d\) 稱為光柵間距，如果 \(N\) 個狹縫佔據總寬度 \(w\)，則 \(d=w/N\)，相鄰光線之間的路徑長度差也是波長整數倍，則亮紋出現： \[d\sin \theta = m \lambda, \quad m=0,1,2,3,... ，(亮紋)\] 其中\(\lambda\)是光的波長，\(\theta\)是平行光與光柵中心軸的夾角。每個整數 \(m\) 代表不同的亮紋；因此這些整數可以用來標記亮紋，如圖所示。整數\(m\)也被稱為級數。因此這些整數可以用來標記線條，如右圖所示，被稱為零階線（中心線，\(m=0\)），一階線（\(m= 1\)），二階線（\(m=2\)），...等等。如果我們重寫方程式。 \(\theta= \sin^{-1}(m \lambda/d)\)，我們看到，對於給定的繞射光柵，從中心軸到任何線（例如，三階線，\(m=3\)）的角度取決於使用光的波長。因此，當未知波長的光通過繞射光柵發送時，透過測量高階亮線的角度，可以決定未知光波的波長。即使照射光原是幾個未知波長的光之混合，也可以用這種方式區分和識別。我們不能用雙縫來做到這一點，即使適用相同的方程式和波長依賴性，在雙縫干涉中，由於波長不同而產生的亮紋重疊過多，無法區分，關於這一點我們可以透過下面的討論還理解。
鑑別率
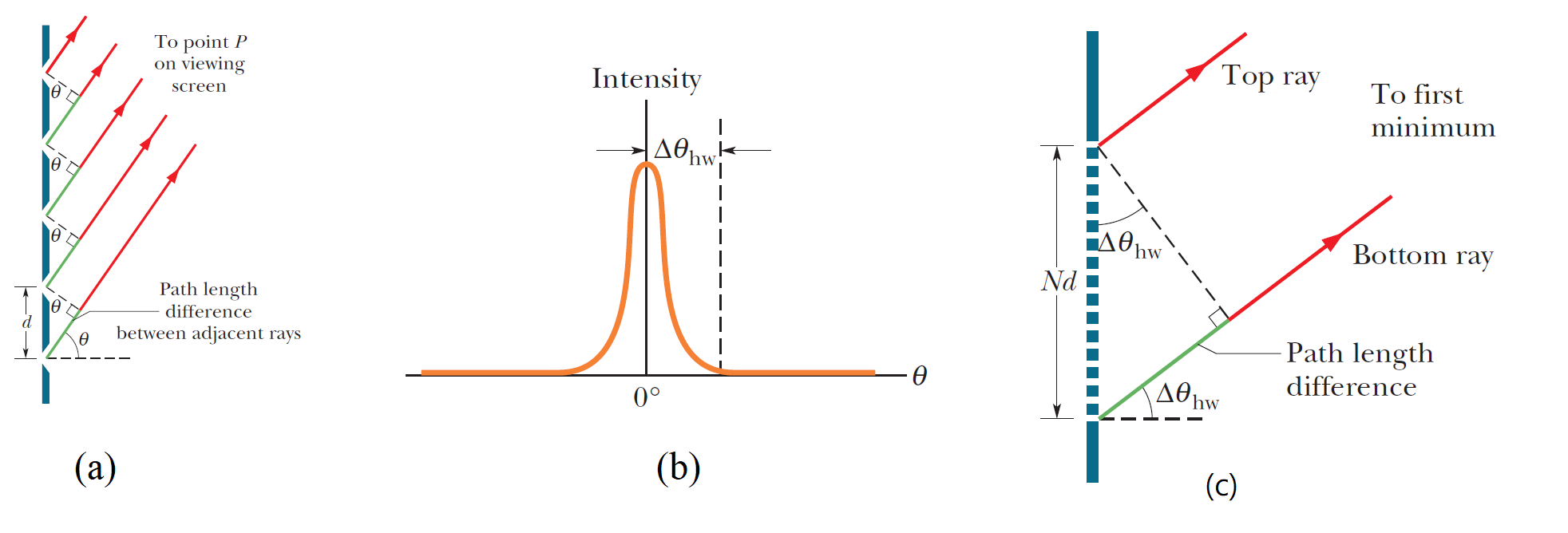
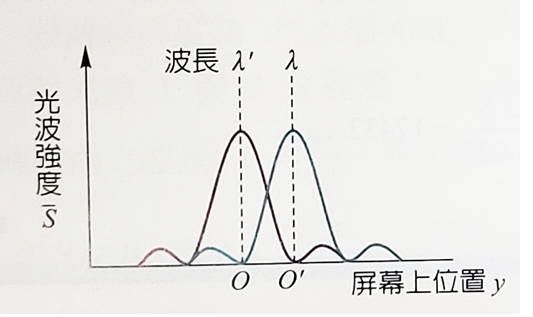假設有波長很接近的兩個光波入射到同一個繞射光柵，若屏幕上出現的干涉圖樣其強度分佈有如右圖所示，也就是一個光波的亮度出現極大值的位置正好是另一個光波第一個亮度極小時出現的位置，則圖中兩光波的亮度尖峰也就是亮度為極大值的位置，恰可清楚的被辨識出來，從而可由其位置差，決定兩波長的差異。
假設照射光柵的狹縫數為\(N\)，兩光波的波長分別為\(\lambda, \, \lambda' = \lambda + \Delta \lambda\)，而且屏幕上出現的\(m\)級干涉圖樣，其光波強度的分佈如右圖，即光波為\(\lambda\)的光波，其中央干涉亮紋正好與\(\lambda'\)光波中央亮紋旁的干涉暗紋在\(O\)點重疊，若\(\theta\)為對應於\(O\)的角位置，那麼我們可以得到下面的關係
\[ d \sin \theta = m \lambda' = (m + \dfrac{1}{N}) \lambda \]
上面的公式經過整理後可得
\[\dfrac{\lambda}{\Delta \lambda}=\dfrac{\lambda}{\lambda' - \lambda}=mN \]
在上面的公式中比值\(\dfrac{\lambda}{\Delta \lambda}\)，可用以衡量光柵將波長很近的兩光譜線分開的能力，所以可以定義為光柵的鑑別率(resolving power)或鑑別本領。從上面的公式我們可以發現鑑別率與干涉級\(m\)和狹縫數\(N\)成正比，鑑別率之值越大，表示可以分辨的波長差越小。例題
原子受到磁場作用時，其發光的光譜線長會一分為二，而在原來的光譜線外，另出現一條波長非常接近的光譜線。假設有一個波長為 435.8 nm 的汞原子光譜線，在磁場中變成波長相差 0.025 nm 的兩條光譜線。若要由一級干涉圖樣分辨出二光譜線則須使用有多少狹縫的繞射光柵？
\[N=\dfrac{\lambda}{m \Delta \lambda}=\dfrac{435.8}{1 \times 0.025}=17432 \]
\[N=\dfrac{\lambda}{m \Delta \lambda}=\dfrac{435.8}{1 \times 0.025}=17432 \]
HL36例題-1
A slit of width \(a\) is illuminated by white light. (a) For what value of \(a\) will the first minimum for red light of wavelength \(\lambda= 650\) nm appear at \(\theta= 15^{\circ}\)? (b) What is the wavelength \(\lambda'\) of the light whose first side diffraction maximum is at \(\theta= 15^{\circ}\), thus coinciding with the first minimum for the red light?
寬度為 \(a\) 的狹縫被白光照亮。 (a) 對於 \(a\) 的值，波長 \(\lambda= 650\) nm 的紅光的第一個最小值將出現在 \(\theta= 15^{\circ}\) 處？ (b) 第一側衍射最大值在 \(\theta= 15^{\circ}\) 處的光的波長 \(\lambda'\) 是多少，因此與紅光的第一個最小值一致？
(a)當我們設置 \(m= 1\) （對於第一個最小值）並替換給定的 \(\theta\) 和 \(\lambda\) 值時，\( a \sin \theta = m \lambda , \quad \text{for}\, m=1,2,3,\cdots\) 產生 \[ a=\dfrac{m\lambda}{\sin \theta}=\dfrac{(1)(650)}{\sin 15^{\circ}}=2511 \, \text{nm}\] (b) 任何波長的第一邊最大值大約在該波長的第一和第二最小值之間。 通過分別設置 \(m = 1\) 和 \(m = 2\)，可以用 \(a \sin \theta= m \lambda\) 定位第一個和第二個最小值。因此，可以通過設置 (m = 1.5\) 來近似定位第一側最大值。 \[a \sin \theta = 1.5 \lambda'\] \[\lambda'=\dfrac{a \sin \theta}{1.5}=\dfrac{(2511)(\sin 15^{\circ}}{1.5}=430 \, \text{nm}\]
寬度為 \(a\) 的狹縫被白光照亮。 (a) 對於 \(a\) 的值，波長 \(\lambda= 650\) nm 的紅光的第一個最小值將出現在 \(\theta= 15^{\circ}\) 處？ (b) 第一側衍射最大值在 \(\theta= 15^{\circ}\) 處的光的波長 \(\lambda'\) 是多少，因此與紅光的第一個最小值一致？
(a)當我們設置 \(m= 1\) （對於第一個最小值）並替換給定的 \(\theta\) 和 \(\lambda\) 值時，\( a \sin \theta = m \lambda , \quad \text{for}\, m=1,2,3,\cdots\) 產生 \[ a=\dfrac{m\lambda}{\sin \theta}=\dfrac{(1)(650)}{\sin 15^{\circ}}=2511 \, \text{nm}\] (b) 任何波長的第一邊最大值大約在該波長的第一和第二最小值之間。 通過分別設置 \(m = 1\) 和 \(m = 2\)，可以用 \(a \sin \theta= m \lambda\) 定位第一個和第二個最小值。因此，可以通過設置 (m = 1.5\) 來近似定位第一側最大值。 \[a \sin \theta = 1.5 \lambda'\] \[\lambda'=\dfrac{a \sin \theta}{1.5}=\dfrac{(2511)(\sin 15^{\circ}}{1.5}=430 \, \text{nm}\]
HL36例題-2
Find the intensities of the first three secondary maxima (side maxima) in the single-slit diffraction pattern of the figure, measured as a percentage of the intensity of the central maximum. 在圖中的單縫衍射圖中找到前三個次級最大值（側最大值）的強度，以中心最大值強度的百分比來衡量。
我們可以通過以下公式將繞射圖案中任意點的強度 \(I\) 與中心最大值的強度\(I_m\)聯繫起來 \[I(\theta)=I_m \left( \dfrac{\sin \alpha}{\alpha} \right)^2,\] \[\alpha=\dfrac{\pi a}{\lambda} \sin \theta .\] 次要最大值大約位於最小值之間，其角度位置由下式給出 \[\text{強度最小值將出現在：} \alpha=m\pi, \quad \text{for } m=1,2,3,\cdots\] \(\alpha\)以弧度為單位。 \[ \dfrac{I}{I_m}=\left( \dfrac{\sin \alpha}{\alpha} \right)^2=\left( \dfrac{\sin (m+\frac{1}{2})\pi}{(m+\frac{1}{2})\pi} \right)^2, \quad \text{for } m=1,2,3,\cdots\] For \(m=1\), \[ \begin{equation} \begin{split} \dfrac{I_1}{I_m} &=\left( \dfrac{\sin (1+\frac{1}{2})\pi}{(1+\frac{1}{2})\pi} \right)^2=\left( \dfrac{\sin 1.5 \pi}{1.5 \pi} \right)^2 &=4.50 \times 10^{-2} \simeq 4.5\% \end{split} \end{equation} \] For \(m=2,3\) we find \[\dfrac{I_2}{I_m}=1.6\%; \quad \dfrac{I_3}{I_m}=0.83\% .\] Successive secondary maxima decrease rapidly in intensity.
HL36例題-3
In a double-slit experiment, the wavelength \(\lambda\) of the light source is 405 nm, the slit separation \(d\) is 19.44 \(\mu\)m, and the slit width a is 4.050 \(\mu\)m. Consider the interference of the light from the two slits and also the diffraction of the light through each slit. (a) How many bright interference fringes are within the central peak of the diffraction envelope? (b) How many bright fringes are within either of the first side peaks of the diffraction envelope?
在雙縫實驗中，光源波長\(\lambda\)為405 nm，縫間距\(d\)為19.44\(\mu\)m，縫寬a為4.050\( \mu\)m。 考慮來自兩個狹縫的光的干涉以及通過每個狹縫的光的繞射。 (a) 繞射包絡的中心峰內有多少明亮的干涉條紋？ (b) 繞射包絡的第一個側峰中有多少條亮條紋？
(a)繞射包絡的中心峰內有多少明亮的干涉條紋
1. 單縫繞射： 中心峰的極限是繞射圖案中的第一個最小值，這是由於任一狹縫單獨造成的。 這些最小值的角位置由 \(a \sin = m \lambda\) 給出。 這裡讓我們將這個方程改寫為 \(a \sin \theta= m_1 \lambda\)，下標 1 指的是單縫繞射。 對於繞射圖中的第一個最小值，我們代入 \(m_1=1\)，得到
\[a \sin \theta = \lambda\]
2.雙縫干涉： 雙縫干涉圖案亮條紋的角位置由
\[d \sin \theta = m_2 \lambda, \quad m_2=0,1,2,\cdots \]
給出，這裡的下標 2 指的是雙縫干涉。
\[m_2=\dfrac{d}{a}=\dfrac{19.44}{4.050}=4.8\]
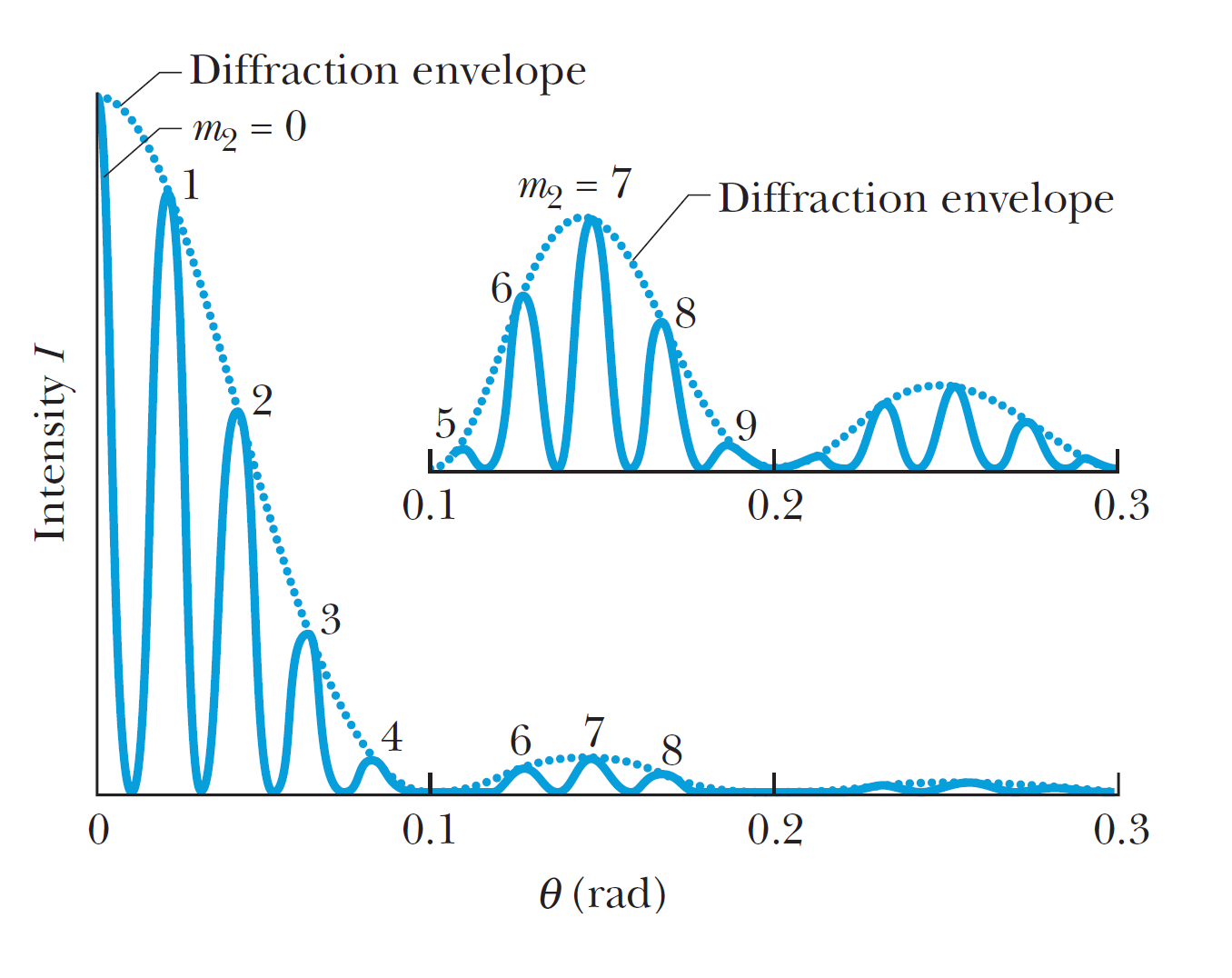
這告訴我們 \(m_2 = 4\) 的明亮干涉條紋適合狹縫繞射圖案，但 \(m_2= 5\) 的條紋不適合。在中心衍射峰內，我們有中心亮條紋 (m_2= 0)，並且在它的每一側都有四個亮條紋（最多 \(m_2 = 4\)）。因此，雙縫干涉圖案共有 9 條亮條紋位於繞射包絡線的中心峰內。中央亮條紋一側的亮條紋如圖所示。
(b)繞射包絡的第一個側峰中有多少條亮條紋
第一面繞射的外邊界峰是第二個繞射最小值，每個是在由 \(a \sin \theta = m_1 \lambda\) 和 \(m_1 = 2\) 給出的角度 \(\theta\) 上： \[ d \sin \theta = 2 \lambda\] \[ m_2 = \dfrac{2d}{a}=\dfrac{(2)(19.44)}{4.05}=9.6 \] 這告訴我們出現了第二個繞射最小值就在 \(m_2 = 10\) 的明亮干涉條紋之前。 在任一第一側繞射峰內，我們都有從 \(m_2 =5 \text{ to } m_2 = 9\) 的條紋，雙縫干涉圖案共有五個明亮的條紋（如圖之插圖所示）. 然而，如果幾乎被第一個繞射最小值消除的\(m_2 = 5\) 亮條紋被認為太暗而無法計數，那麼只有4個亮條紋位於第一側繞射峰中。
在雙縫實驗中，光源波長\(\lambda\)為405 nm，縫間距\(d\)為19.44\(\mu\)m，縫寬a為4.050\( \mu\)m。 考慮來自兩個狹縫的光的干涉以及通過每個狹縫的光的繞射。 (a) 繞射包絡的中心峰內有多少明亮的干涉條紋？ (b) 繞射包絡的第一個側峰中有多少條亮條紋？
(a)繞射包絡的中心峰內有多少明亮的干涉條紋
(b)繞射包絡的第一個側峰中有多少條亮條紋第一面繞射的外邊界峰是第二個繞射最小值，每個是在由 \(a \sin \theta = m_1 \lambda\) 和 \(m_1 = 2\) 給出的角度 \(\theta\) 上： \[ d \sin \theta = 2 \lambda\] \[ m_2 = \dfrac{2d}{a}=\dfrac{(2)(19.44)}{4.05}=9.6 \] 這告訴我們出現了第二個繞射最小值就在 \(m_2 = 10\) 的明亮干涉條紋之前。 在任一第一側繞射峰內，我們都有從 \(m_2 =5 \text{ to } m_2 = 9\) 的條紋，雙縫干涉圖案共有五個明亮的條紋（如圖之插圖所示）. 然而，如果幾乎被第一個繞射最小值消除的\(m_2 = 5\) 亮條紋被認為太暗而無法計數，那麼只有4個亮條紋位於第一側繞射峰中。
HL36例題-4
衍射光柵具有在寬度 \(w = 25.4\) mm 上均勻分佈的 \(1.26 \times 10^4\) 刻線。 它由鈉蒸氣燈發出的黃光以法向入射照明。 這種光包含兩條間隔很近的發射線（稱為鈉雙峰），波長分別為 589.00 nm 和 589.59 nm。
(a) 對於 589.00 nm 的波長，一級最大值出現在什麼角度（在衍射圖案中心的兩側）？
(b) 利用光柵的色散，一階計算兩條線之間的角距。
(c) 光柵可以具有並且仍然能夠在一階分辨鈉雙峰的最少刻線數是多少？
(a)The maxima produced by the diffraction grating can be determined with Eq\(d \sin \theta = m \lambda\). The first-order maximum corresponds to \(m=1\).
\[d=\dfrac{w}{N}=\dfrac{25.4 \times 10^{-3}}{1.26 \times 10^4}=2.016 \times 10^{-6} \, \text{m}=2016 \, \text{nm}\] \[ d \sin \theta = m \lambda; \quad \theta=\sin^{-1} \dfrac{m \lambda}{d}=\sin^{-1} \dfrac{(1)(589)}{2016}=16.99^{\circ} \] (b)(1) The angular separation \(\Delta \theta\) between the two lines in the first order depends on their wavelength difference \(\Delta \lambda\) and the dispersion \(D\) of the grating, according to Eq.: \(D=\Delta \theta/ \Delta \lambda\). (2) The dispersion D depends on the angle \(\theta\) at which it is to be evaluated.
\[\Delta \theta=D \Delta \lambda=(5.187 \times 10^{-4})(589.59 - 589.00)\\ =3.06 \times 10^{-4} \, \text{rad}=0.0175^{\circ}\] (c)(1) The resolving power of a grating in any order \(m\) is physically set by the number of rulings \(N\) in the grating according to Eq. \(R=Nm\). (2) The smallest wavelength difference \(\Delta \lambda\) that can be resolved depends on the average wavelength involved and on the resolving power \(R\) of the grating, according to Eq.: \(R =\lambda_{avg} / \Delta \lambda\).
\[N=\dfrac{R}{m}=\dfrac{R}{m}==\dfrac{\lambda_{avg}}{m \Delta \lambda} \\ =\dfrac{589.3}{(1)(0.59)}=999\]
(a) 對於 589.00 nm 的波長，一級最大值出現在什麼角度（在衍射圖案中心的兩側）？
(b) 利用光柵的色散，一階計算兩條線之間的角距。
(c) 光柵可以具有並且仍然能夠在一階分辨鈉雙峰的最少刻線數是多少？
(a)The maxima produced by the diffraction grating can be determined with Eq\(d \sin \theta = m \lambda\). The first-order maximum corresponds to \(m=1\).
\[d=\dfrac{w}{N}=\dfrac{25.4 \times 10^{-3}}{1.26 \times 10^4}=2.016 \times 10^{-6} \, \text{m}=2016 \, \text{nm}\] \[ d \sin \theta = m \lambda; \quad \theta=\sin^{-1} \dfrac{m \lambda}{d}=\sin^{-1} \dfrac{(1)(589)}{2016}=16.99^{\circ} \] (b)(1) The angular separation \(\Delta \theta\) between the two lines in the first order depends on their wavelength difference \(\Delta \lambda\) and the dispersion \(D\) of the grating, according to Eq.: \(D=\Delta \theta/ \Delta \lambda\). (2) The dispersion D depends on the angle \(\theta\) at which it is to be evaluated.
\[\Delta \theta=D \Delta \lambda=(5.187 \times 10^{-4})(589.59 - 589.00)\\ =3.06 \times 10^{-4} \, \text{rad}=0.0175^{\circ}\] (c)(1) The resolving power of a grating in any order \(m\) is physically set by the number of rulings \(N\) in the grating according to Eq. \(R=Nm\). (2) The smallest wavelength difference \(\Delta \lambda\) that can be resolved depends on the average wavelength involved and on the resolving power \(R\) of the grating, according to Eq.: \(R =\lambda_{avg} / \Delta \lambda\).
\[N=\dfrac{R}{m}=\dfrac{R}{m}==\dfrac{\lambda_{avg}}{m \Delta \lambda} \\ =\dfrac{589.3}{(1)(0.59)}=999\]
授課教師
陳永忠 ycchen@thu.edu.tw