線性代數2:行列式與反矩陣

1. 行列式

行列式（Determinant）是數學中的一個函數，將一個\( n\times n \)的矩陣A映射到一個純量，記作\( \det(A)\) 或 \( |A| \)。 一個n階方塊矩陣A的行列式可直觀地定義如下： \[ \det(A)=\sum_{\sigma \in S_{n}} \operatorname{sgn}(\sigma )\prod _{i=1}^{n}a_{i,\sigma (i)} \] 其中， \(S_n\)是集合 \( \left\{1,2,...,n\right\} \) 上置換(permutation)的全體。 舉例來說，對於3元置換\(\sigma=(2,3,1)\) (即是說 \( \sigma (1)=2, \sigma(2)=3, \sigma(3)=1\) )而言，由於1在2後，1在3後，所以共有2個逆序（偶數個），因此\(\operatorname{sgn}(\sigma)=1\)，從而3階行列式中項 \( a_{1,2}a_{2,3}a_{3,1} \) 的符號是正的。但對於三元置換 \( \sigma =\left(3,2,1\right)\)（即是說 \( \sigma (1)=2, \sigma(2)=3, \sigma(3)=1\)）而言，可以數出共有3個逆序（奇數個），因此 \( \operatorname {sgn} \sigma =-1\)，從而3階行列式中項 \( a_{1,3}a_{2,2}a_{3,1} \)的符號是負號。 注意到對於任意正整數n， \( S_{n}\)共擁有n!個元素，因此上式中共有n!個求和項。

• 2階矩陣的行列式：
  \( {\begin{vmatrix}a_{1,1}&a_{1,2}\\a_{2,1}&a_{2,2}\end{vmatrix}}=a_{1,1}a_{2,2}-a_{1,2}a_{2,1} \)
• 3階矩陣的行列式：
  \( \begin{vmatrix}a_{1,1}&a_{1,2}&a_{1,3}\\a_{2,1}&a_{2,2}&a_{2,3}\\a_{3,1}&a_{3,2}&a_{3,3}\end{vmatrix}\\=a_{1,1}a_{2,2}a_{3,3}+a_{1,2}a_{2,3}a_{3,1}+a_{1,3}a_{2,1}a_{3,2}\\-a_{1,3}a_{2,2}a_{3,1}-a_{1,1}a_{2,3}a_{3,2}-a_{1,2}a_{2,1}a_{3,3} \)


在我們實際的應用中，numpy有一個函數副程式，np.linalg.det可以直接使用來計算矩陣的行列式值

np.linalg.det(A)

2. 反矩陣

So basically the matrix inverse problem can be reformulated as a LSE(Linear System of Equations) solving problem:
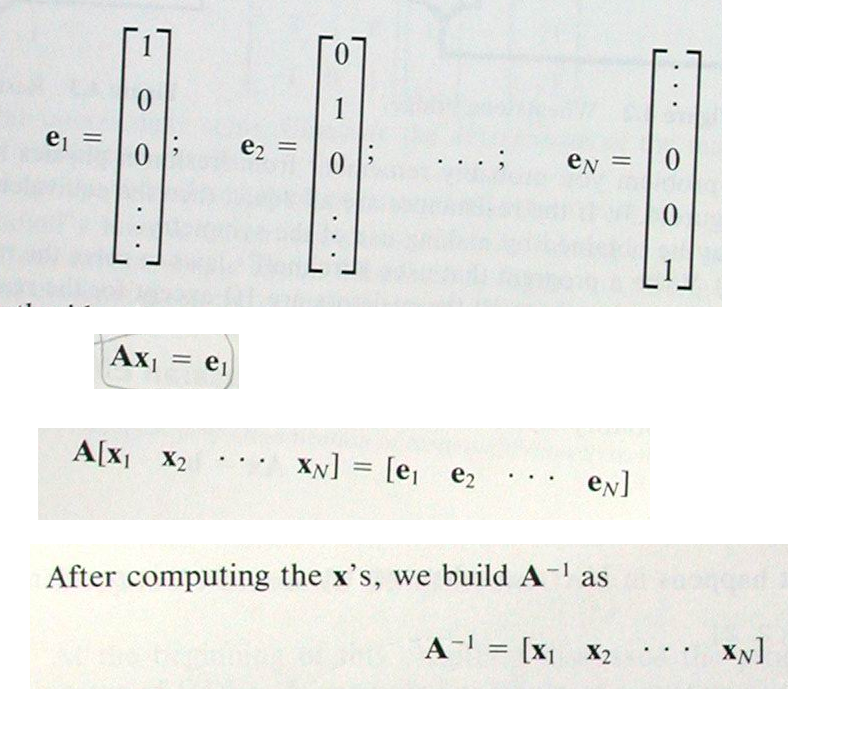
For each \(\mathbf{b}_i\) we solve the following matrix equation: \[ \mathbf{Ax}_i = \mathbf{b}_i \] \(\mathbf{x}_i\) is the i-th column vector of the inverse matrix \(\mathbf{A}^{-1}\). Once we solved all \(\mathbf{x}_i\) we obtain the inverse of \(\mathbf{A}\), i.e., \(\mathbf{A}^{-1}\).

在我們實際的應用中，numpy有一個函數副程式，np.linalg.inv可以直接使用來計算反矩陣

A_inverse = np.linalg.inv(A)





---

import numpy as np
A=np.mat([[2,-2,0],
          [-2,1,-2],
          [0,-2,0]])
print 'A=\n',A
detA=np.linalg.det(A)    #計算行列式
print '\n\nUse np.linalg.det to get det(A)=',detA
Ai=np.linalg.inv(A)    #計算反矩陣/pR>
print '\n\nUse np.linalg.inv to get Ai=\n',Ai

I=np.dot(Ai,A)    #計算矩陣相乘，驗證Ai乘A等於I,單位矩陣
print '\n\nUse np.dot(Ai,A) to check identity mat, I=\n',I








---

import numpy as np

# function inverse is defined to calculate the inverse 
# matrix by solving LSE
def inverse(N,a):
    z=[]
    for i in range(N):
        a0=a
        b=[0 for j in range(N)]
        b[i]=1
        x=np.linalg.solve(a0, b)
        I=np.dot(a, x)
        z.append(x)
    a1=np.array([z[i] for i in range(N)])
    ai=a1.transpose()
    return ai

a = np.array([[3,1], [1,2]])
ai=inverse(2,a)
print 'use inverse, ai_2x2=\n',ai
print 'np.linalg.inv(a)=\n',np.linalg.inv(a)


# solve 3x3  cy=d
c = np.array([[1,1,1], [3,1,0], [-1,0,1]])
ci=inverse(3,c)
print 'use inverse, ci_3x3=\n',ci
print 'np.linalg.inv(c)=\n',np.linalg.inv(c)
print 'check c dot ci=I=\n',np.dot(c, ci)