常微分方程

    1. 非齊次一階常係數線性微分方程式：
      2. \[\frac{du}{dx}=cu+x^{2}. \]
    2. 齊次二階線性微分方程式：
      3. \[\frac{d^{2}u}{dx^{2}}-x\frac{du}{dx}+u=0. \]
    3. 描述諧振子的齊次二階常係數線性微分方程式：
      4. \[\frac {d^{2}u}{dx^{2}}+\omega^{2}u=0. \]
    4. 非齊次一階非線性微分方程式：
      5. \[ \frac {du}{dx}=u^{2}+1. \]
    5. 描述長度為\(L\)的單擺的二階非線性微分方程式：
      6. \[ L\frac {d^{2}u}{dx^{2}}+g\sin u=0. \]

    1. 用原始的python語言設計積分的程式

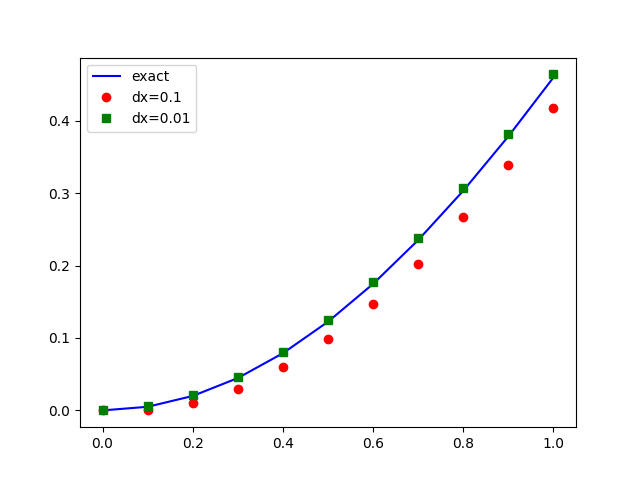
    微分方程式的解通常是一個函數表達式\(y=f(x)\,\),（含一個或多個待定常數，由初始條件確定）。例如： \[\frac{dy}{dx}=\sin x\] 的解是 \[ y=-\cos x+C\] 其中\(C\)是待定常數；例如，如果知道 \[ y=f(\pi )=2 \] 則可推出\(C=1\)，而可知 \( y=-\cos x+1 \)。 \[dy=\sin(x)\, dx\] \[y(x+dx)-y(x)=\sin(x) dx\] \[y(x+dx)=y(x)+\sin(x) dx\] \[x=0; \,\, y(0)=0, dx=0.1\] \[y(0.1)=y(0)+\sin(0.1)(0.1)=0\] \[y(0.2)=y(0.1)+\sin(0.1)(0.1)=0.01\] \[y(0.3)=y(0.2)+\sin(0.2)(0.1)=0.0299\] \[y(0.4)=y(0.3)+\sin(0.3)(0.1)=0.0594\] 
       0   0.0000   0.0000   0.0000
   1   0.1000   0.0000   0.0050
   2   0.2000   0.0100   0.0199
   3   0.3000   0.0299   0.0447
   4   0.4000   0.0594   0.0789
   5   0.5000   0.0983   0.1224
   6   0.6000   0.1463   0.1747
   7   0.7000   0.2028   0.2352
   8   0.8000   0.2672   0.3033
   9   0.9000   0.3389   0.3784
  10   1.0000   0.4172   0.4597



    import numpy as np
import matplotlib
import matplotlib.pyplot as plt
dx=0.1
y=0; x=0; xp=[]; y1p=[]; y2p=[]; yxp=[]
for i in range(11):
    yex=-np.cos(x)+1
    xp.append(x); y1p.append(y); yxp.append(yex)
    print('%4d %8.4f %8.4f %8.4f' %(i,x,y,yex))
    y1=y+np.sin(x)*dx
    x+=dx
    y=y1

dx=0.01
y=0; x=0
for i in range(101):
    yex=-np.cos(x)+1
    if(i%10==0):
        y2p.append(y)
        print('%4d %8.4f %8.4f %8.4f' %(i,x,y,yex))
    x+=dx
    y1=y+np.sin(x)*dx
    y=y1
plt.plot(xp,yxp,'b-',label='exact')
plt.plot(xp,y1p,'ro',label='dx=0.1')
plt.plot(xp,y2p,'gs',label='dx=0.01')
plt.legend()
plt.savefig("ODE-1-numpy.png")
print ('plot is done')


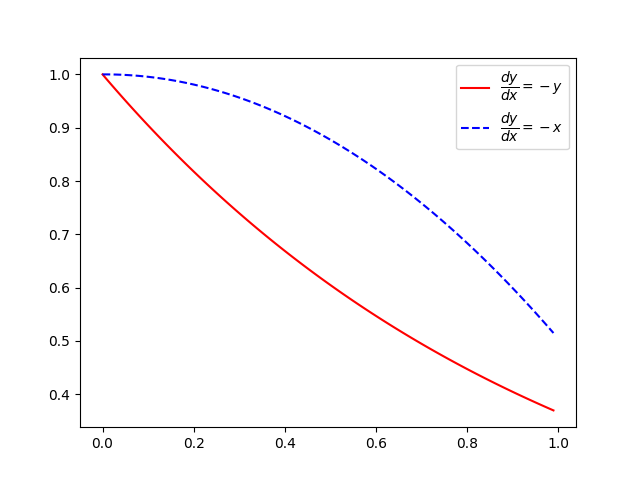
    \(\frac{dy}{dx}=-y;\)    \(\frac{dy}{dx}=-x;\)
    initial condition: \(y(0)=1\) 
    import numpy as np
import matplotlib
import matplotlib.pyplot as plt
def deriv1(xi,yi):
    return -yi
def deriv2(xi,yi):
    yi=-xi
    return yi
def sol(x,dx,y0,N,deriv):
    y=[0 for i in range(N)]
    y[0]=y0
    for i in range(1,N):
        x1=x[i-1]
        y1=y[i-1]
        y[i]=y[i-1]+deriv(x1,y1)*dx
    return y
a=0;b=1;dx=0.01
x=np.arange(a,b,dx)
N=len(x)
y0=1
y1=sol(x,dx,y0,N,deriv1)
y2=sol(x,dx,y0,N,deriv2)
plt.plot(x,y1,'r-', label=r'$\dfrac{dy}{dx}=-y$')
plt.plot(x,y2,'b--',label=r'$\dfrac{dy}{dx}=-x$')
plt.legend()
plt.savefig("ODE-2-numpy.png")
print ('plot is done')


    2. sympy解微分方程：

    from sympy import *
init_printing()
t= symbols('t')
y = Function('y')(t)
dydt = y.diff(t)
expr = Eq(dydt, sin(t))
print('expr=',expr)
pprint(expr)
sol=dsolve(expr)
print('sol=',sol)
pprint(sol)



    from sympy import *
init_printing()
keq=2
if(keq==1):
    t= symbols('t')
    y = Function('y')(t)
    y1 = y.diff(t)
    expr = Eq(y1, sin(t))
if(keq==2):
    t= symbols('t')
    y = Function('y')(t)
    y1 = y.diff(t)
    expr = Eq(y1, exp(3*t)+y)
if(keq==3):
    t= symbols('t')
    y = Function('y')(t)
    y1 = y.diff(t)
    y2 = y1.diff(t)
    expr = Eq(y2, -y)
if(keq==4):
    t= symbols('t')
    y = Function('y')(t)
    y1 = y.diff(t)
    expr = Eq(y1, y**2+1)
if(keq==5):
    t= symbols('t')
    y = Function('y')(t)
    y1 = y.diff(t)
    expr = Eq(y1, y/(t**2+1))

print('expr=',expr)
pprint(expr)
sol=dsolve(expr)
print('sol=',sol)
pprint(sol)


    請同學們自己用sympy練習解下面的微分方程：

    1. \(\frac{dy}{dx}=\frac{y}{1+x^2}; \,\,\, \rightarrow y(x)=C_1 e^{\tan^{-1} x}\)

    2. \(\frac{dy}{dx}=y+e^{3x}; \,\,\, \rightarrow y(x)=C e^x + \frac{1}{2}e^{3x}\)

    3. \(\frac{dy}{dx}=\frac{3x^2-2x+1}{y^3+2y}; \,\,\, \rightarrow y^4/4+y^2=x^3-x^2+x+C\)






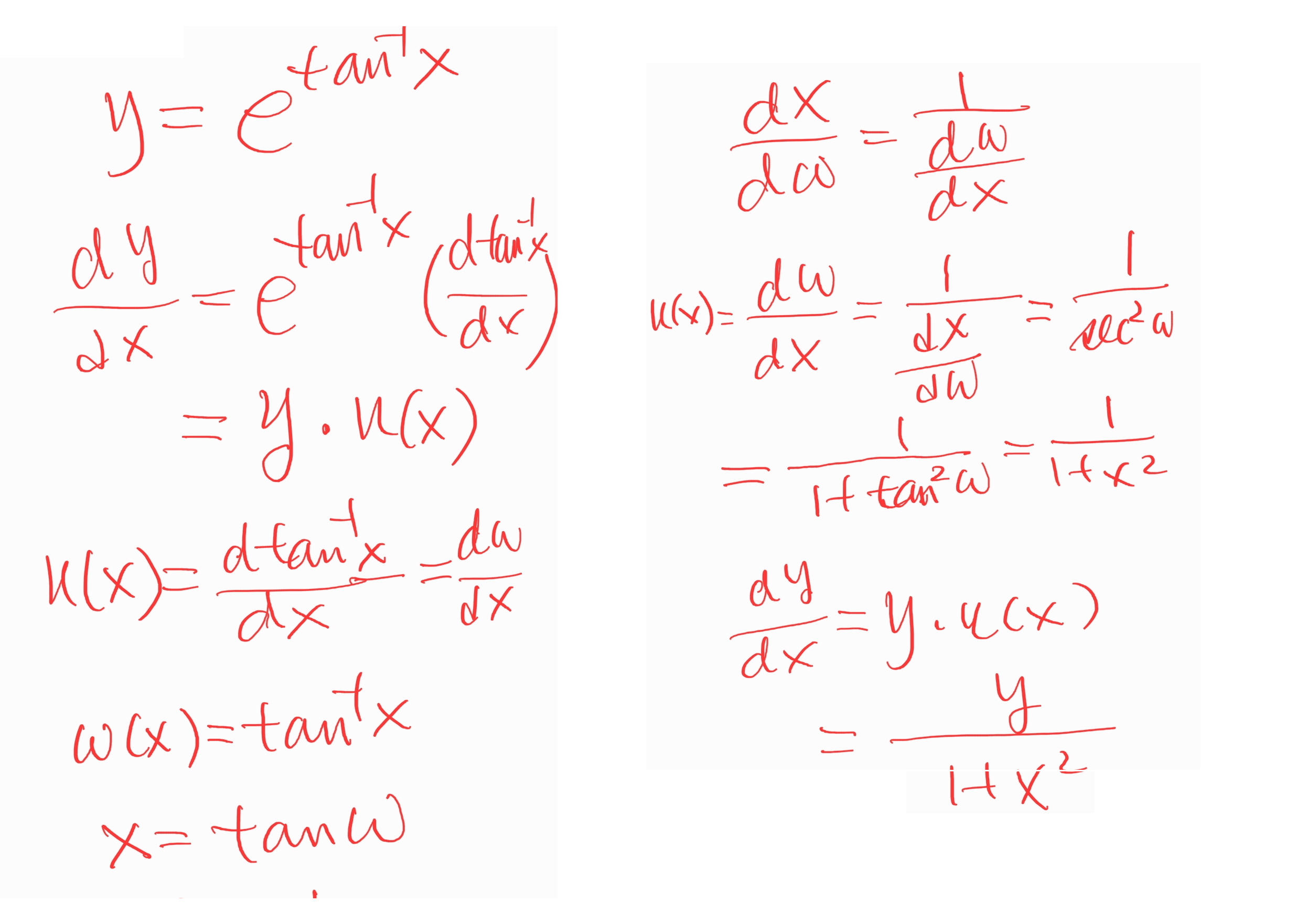
    3. scipy解微分方程：

    import numpy as np 
from scipy.integrate import odeint 
import matplotlib.pyplot as plt 
from scipy.integrate import odeint
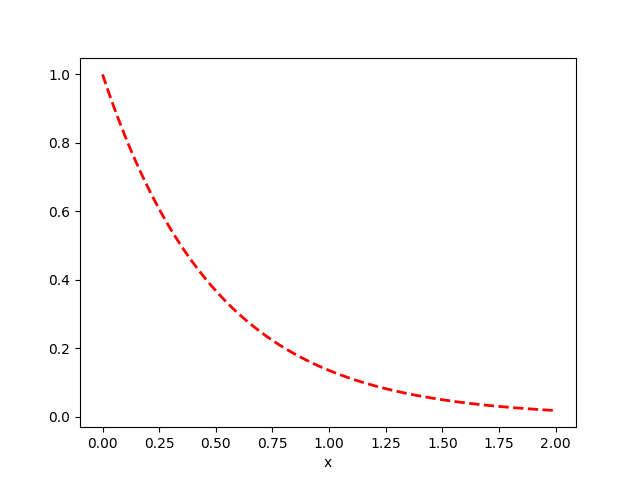
def f(x,t):
    return -2*x
x0=1 # initial value
a=0 # integration limits for t, a < t < b
b=2
t=np.arange(a, b, 0.01) # values of t for
x=odeint(f,x0,t) # actual computation of x(t)
plt.plot(t,x,'r--', linewidth=2.0) 
plt.xlabel("t") 
plt.xlabel("x") 
plt.savefig("ODE_1_sci.png")
print ('plot is done')



    import numpy as np 
from scipy.integrate import odeint 
import matplotlib.pyplot as plt 
from scipy.integrate import odeint
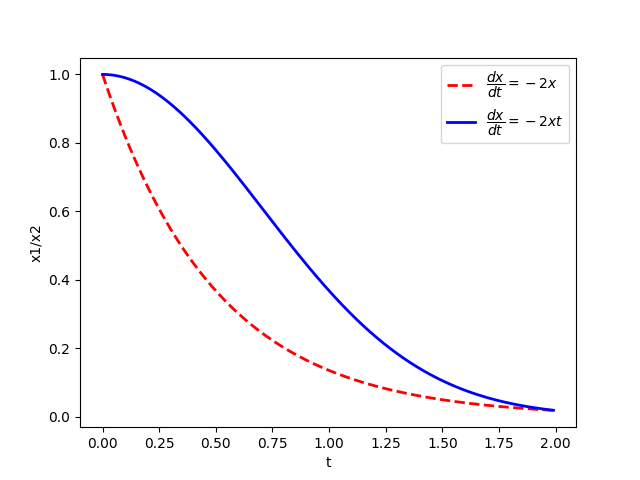
def f1(x,t):
    return -2*x
def f2(x,t):
    return -2*x*t
x0=1; a=0 ; b=2
t=np.arange(a, b, 0.01) 
x1=odeint(f1,x0,t) 
x2=odeint(f2,x0,t) 
plt.plot(t,x1,'r--', linewidth=2.0, label=r"$\dfrac{dx}{dt}=-2x$") 
plt.plot(t,x2,'b-',  linewidth=2.0, label=r"$\dfrac{dx}{dt}=-2xt$") 
plt.xlabel("t") 
plt.ylabel("x1/x2") 
plt.legend()
plt.savefig("ODE_2_sci.png")
print ('plot is done')


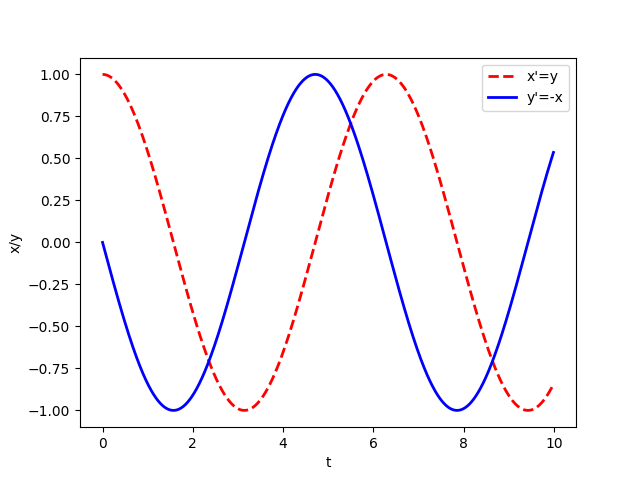
    微分方程的耦合系統： \[\frac{d^2 x}{dt^2}=-x\] \[\frac{dx}{dt}=y\] \[\frac{dy}{dt}=-x\] 
    import numpy as np 
from scipy.integrate import odeint 
import matplotlib.pyplot as plt 
from scipy.integrate import odeint
mu=0
def SHO(X, t):
    x = X[0]
    y = X[1]
    dxdt = y
    dydt = -x
    return [dxdt, dydt]
X0=[1,0]
a=0 
b=10
t=np.arange(a, b, 0.01) 
sol = odeint(SHO, X0, t)
x = sol[:, 0]
y = sol[:, 1]
plt.plot(t,x,'r--', linewidth=2.0, label="x'=y") 
plt.plot(t,y,'b-', linewidth=2.0, label="y'=-x") 
plt.xlabel("t") 
plt.ylabel("x/y") 
plt.legend()
plt.savefig("ODE_3_sci.png")
print ('plot is done')


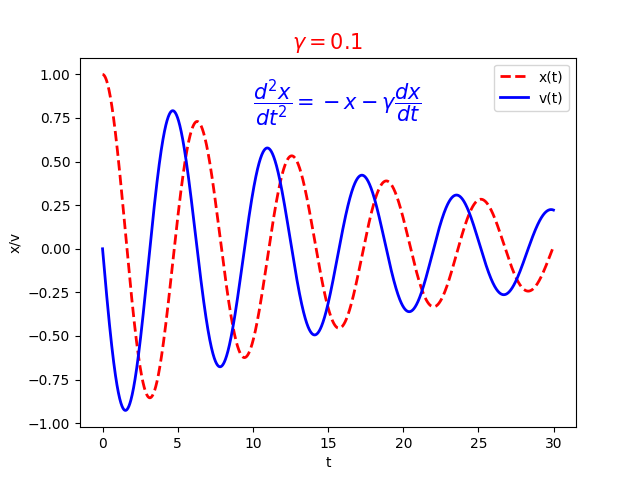
    阻尼震盪：

    受驅阻尼振子滿足方程式 \[\frac{\mathrm{d}^{2}x}{\mathrm{d} t^{2}}+\frac {\mathrm {d} x}{\mathrm {d} t}+kx=F_{0}\cos(\omega t)\] 其一般解為兩個解的和，一為暫態解（無驅動阻尼諧振子之齊次常微分方程式的解），與初始條件相關；另一為穩態解（非齊次常微分方程式之特殊解），與初始條件無關，只與驅動頻率、驅動力、阻尼力有關。 穩態解為 \[ x(t)={\frac {F_{0}}{Z_{m}\omega }}\sin(\omega t-\phi )\] 其中 \[ Z_{m}={\sqrt {r^{2}+\left(\omega m-{\frac {k}{\omega }}\right)^{2}}}\] 為阻抗（impedance）或線性響應函數（linear response function）之絕對值 而 \[ \phi =\arctan \left({\frac {\omega m-{\frac {k}{\omega }}}{r}}\right)\] 為相對於驅動力（相位定為0）的振動相位。 可以觀察到，當在某特定驅動頻率 \(\omega\) 時，振子振動之振幅（相對於一給定之\( F_{0}\)）達到最大。這發生在頻率為 \[\omega_{r}=\sqrt{\frac {k}{m}-2\left(\frac{r}{2m}\right)^{2}}\] 之時，而此現象稱之為（位移上的）共振。 
    import numpy as np 
from scipy.integrate import odeint 
import matplotlib.pyplot as plt 
from scipy.integrate import odeint
gamma=0.1
def SHO(X, t):
    x = X[0]
    v = X[1]
    dxdt = v
    dvdt = -x-gamma*v
    return [dxdt, dvdt]
X0=[1,0]
a=0 
b=30
t=np.arange(a, b, 0.01) 
sol = odeint(SHO, X0, t)
x = sol[:, 0]
v = sol[:, 1]
plt.plot(t,x,'r--', linewidth=2.0, label="x(t)") 
plt.plot(t,v,'b-',  linewidth=2.0, label="v(t)") 
plt.title(r'$\gamma=0.1$', color='red', fontsize=15)
plt.text(10, 0.8,r'$\dfrac{d^2x}{dt^2}=-x-\gamma \dfrac{dx}{dt}$', \
     color='b', fontsize=15)
plt.xlabel("t") 
plt.ylabel("x/v") 
plt.legend()
plt.savefig("ODE_SHO_sci.png")
print ('plot is done')


    \(\frac{d^2x}{dt^2} - \mu(1-x^2)\frac{dx}{dt} + x = 0\)
    微分方程的耦合系統： 
    import numpy as np 
from scipy.integrate import odeint 
import matplotlib.pyplot as plt 
def f(s,t): 
    a = 4; b = 7 ; n = s[0] ; c = s[1] 
    dndt = a * n - (c/(c+1)) * b * n 
    dcdt = (c/(c+1)) * n - c + 1 
    return [dndt, dcdt] 
t = np.linspace(0,20) 
s0=[20,5] 
s = odeint(f,s0,t) 
plt.plot(t,s[:,0],'r--', linewidth=2.0) 
plt.plot(t,s[:,1],'b-', linewidth=2.0) 
plt.xlabel("t") 
plt.ylabel("S[N,C]") 
plt.legend(["N","C"]) 
plt.savefig("ODE_3_sci.png")
print ('plot is done')




    5. sympy函數轉換為numpy

    from sympy import *
init_printing()
init_printing(use_unicode=False, wrap_line=False)
x = symbols('x')
IG=x**2+x+1
I=integrate(IG, x)
print(IG)
print(I)
pprint(IG)
pprint(I)

import numpy as np
import matplotlib.pyplot as plt
fsyIG = lambdify(((x),), IG)
fsyI = lambdify(((x),), I)
N=101; a=0; b=10
t=np.linspace(a,b,N)
npIG=fsyIG(t)
npI=fsyI(t)
plt.figure()
plt.plot(t,npIG,'r--',label="IG")
plt.plot(t,npI,'b-',label="I")
plt.legend()
plt.savefig('sympy-matplot-1.png')
print('plot sympy to np,matplot is done')


    Exercise

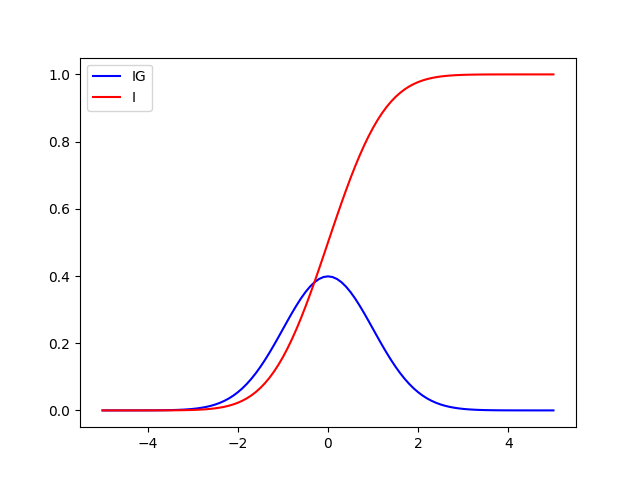
    Use numpy and sympy to complete the integration below: \[ I(x)=\int_{-\infty}^x \frac{1}{\sqrt{2\pi}}e^{-t^2 /2} \,dt\] Find \(I(x)\) and make the plot of the integrand(IG), \(\frac{1}{\sqrt{2\pi}}e^{-x^2 /2}\) and \(I(x)\).