電場與庫倫定律的應用

我們知道電荷的存在會在空間中建立起一個電場，最簡單的電荷源就是電點荷。描述單一一個電荷所建立的電場的基本定律就是庫倫定律。一般我們所看到最簡單的庫倫定律的形式如下： \[\vec{E}=\frac{kq}{r^2}\hat{r}=\frac{kq}{r^3}\vec{r} \] 請注意在上面這個公式中我們用了一個非常重要的向量關係，那就是位置向量(\(\vec{r}\))的單位向量(\(\hat{r}\))等於位置向量處理位置向量的長度(\(|\vec{r})\))，而且還要注意到上面這個公式，以坐標系統的原點就在點電荷的位置，來描述空間中場的位置向量，如果我們在空間中有許多的電荷，那麼這個公式就不適合來描述這樣的情況。所以比較好的庫倫定律的寫法應該是下面的公式。

座標的原點不在點電荷q上面，所以點電荷q有自己的位置向量(\(\vec{r}'\))，欲計算的電場位置有向量是以\(\vec{r}\)來描述，電場本身也是一個向量(\(\vec{E}\))，其方向及大小與空間中的位置有關，位置\(\vec{r}\)的電場向量是\(\vec{r}\)的函數，當然也是x,y,z的函數： \[\vec{E}(\vec{r})=\frac{kq}{|\vec{r}-\vec{r}'|^3}(\vec{r}-\vec{r}') \] 如果我們有很多的電荷那麼就把這個公式推廣一下，就得到多個點電荷在空間在空間中所建立的電場： \[\vec{E}(\vec{r})=\sum_i \frac{kq}{|\vec{r}-\vec{r_i}'|^3}(\vec{r}-\vec{r_i}') \] 在我們下面的程式中就是反覆的應用這個電場公式來計算單一一個點電荷，或是有多個電荷分佈成不同的幾何形狀時，在空間中分別建立起不同的電場。在普通物理中我們已經學過，單一點電荷所建立的電場大小，隨著與電荷距離的變化是平方反比定律；但是如果把電荷均勻地排成一條無窮長的直線時，那麼電廠的大小與距離成1次方反比定律；如果把電荷平均地分佈在一個平面上，那麼這個平面將會造就出一個常數的電場，電場大小與距離完全無關。如果我們有一個正電荷和一個負電荷分隔一段距離形成一個所謂的電偶極，那麼在遠離這個電偶極的地方去測量電場的話，會發現電場的大小隨著遠離電偶極的距離是3次方反比定律。我們希望能夠藉由下面的數值計算來驗證這些重要結果。

  1. 單一點電荷所建立的電場

    2.  
    import numpy as np
def EF_point(q,rq,r):
    ke=1.
    rrq=r-rq
    rrq0=np.linalg.norm(rrq)
    Es=ke*q/rrq0**2
    E=ke*q*rrq/rrq0**3
    return E,Es
q=1.
rq=np.array([0.,0.,0.])

r1=np.array([1,0,0])
E1,E1s=EF_point(q,rq,r1)
print(r1,E1,E1s)

r2=np.array([1,1,0])
E2,E2s=EF_point(q,rq,r2)
print(r2,E2,E2s)

r3=np.array([1,1,1])
E3,E3s=EF_point(q,rq,r3)
print(r3,E3,E3s)

    ============輸出:=============

    

    [1 0 0] [1. 0. 0.] 1.0
[1 1 0] [0.35355339 0.35355339 0.        ] 0.4999999999999999
[1 1 1] [0.19245009 0.19245009 0.19245009] 0.33333333333333337



  2. zip內建函數

    3.  zip()是python的一個內建函數，它接受一系列可迭代的對象作為參數，將對象中對應的元素打包成一個tuple(元組)，然後返回由這些tuple組成的列表內容。若傳入參數的長度不等的時候，則返回與列表長度最短的對象。這個函數對我們後面用在向量的處理非常好用。 
    numbers=[1,2,3]
letters=['a','b','c']
zipped=zip(numbers,letters)
for n,l in zipped:
    print(n,l)
print('---------')
#zipped=zip(numbers,letters)
for n,l in zipped:
    print(l,n)
print('---------')

a=[1,2,3]
b=[4,5,6]
c=[4,5,6,7,8]
zip2=zip(a,b)
zip3=zip(a,b,c)
for x,y in zip2:
    print(x,y)
for x,y,z in zip3:
    print(x,y,z)

    ============輸出:=============

    

    1 a
2 b
3 c
---------
---------
1 4
2 5
3 6
1 4 4
2 5 5
3 6 6



  3. 點電荷沿著+x方向的電場

    4.  在這個範例程式中我們結合numpy array, zip(), list的用法，把點電荷在正x方向所建立的電場計算出來並且畫成圖。 
    import matplotlib
matplotlib.use("Agg")
import matplotlib.pyplot as plt
import numpy as np

sin=np.sin; cos=np.cos; pi=np.pi
def EF_point(q,rq,r):
    ke=1.
    rrq=r-rq
    rrq0=np.linalg.norm(rrq)
    Es=ke*q/rrq0**2
    E=ke*q*rrq/rrq0**3
    return E,Es
q=1.
rq=np.array([0.,0.,0.])
rx=np.linspace(0.5,5,20)
ry=np.zeros_like(rx)
rz=np.zeros_like(rx)
for x,y,z in zip(rx,ry,rz):
    r=np.array([x,y,z])
    Ev,Es=EF_point(q,rq,r)
    plt.plot(x,Es,'k-o')
    plt.plot(x,Ev[0],'r-o')
    print(r,Ev)
plt.savefig("EF-03.png")
print('plot is done.')  

    ============輸出:=============

    

    [0.5 0.  0. ] [4. 0. 0.]
[0.73684211 0.         0.        ] [1.84183673 0.         0.        ]
[0.97368421 0.         0.        ] [1.05478451 0.         0.        ]
[1.21052632 0.         0.        ] [0.68241966 0.         0.        ]
[1.44736842 0.         0.        ] [0.47735537 0.         0.        ]
[1.68421053 0.         0.        ] [0.35253906 0.         0.        ]
[1.92105263 0.         0.        ] [0.27097016 0.         0.        ]
[2.15789474 0.         0.        ] [0.21475312 0.         0.        ]
[2.39473684 0.         0.        ] [0.17437508 0.         0.        ]
[2.63157895 0.         0.        ] [0.1444 0.     0.    ]
[2.86842105 0.         0.        ] [0.12153859 0.         0.        ]
[3.10526316 0.         0.        ] [0.10370583 0.         0.        ]
[3.34210526 0.         0.        ] [0.08952818 0.         0.        ]
[3.57894737 0.         0.        ] [0.07807093 0.         0.        ]
[3.81578947 0.         0.        ] [0.06868014 0.         0.        ]
[4.05263158 0.         0.        ] [0.06088716 0.         0.        ]
[4.28947368 0.         0.        ] [0.05434905 0.         0.        ]
[4.52631579 0.         0.        ] [0.04881017 0.         0.        ]
[4.76315789 0.         0.        ] [0.0440768 0.        0.       ]
[5. 0. 0.] [0.04 0.   0.  ]
plot is done.



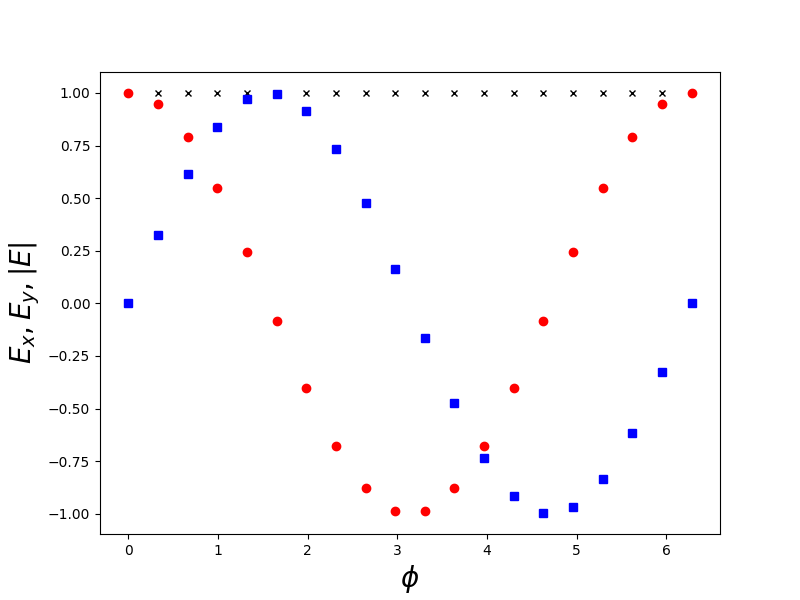
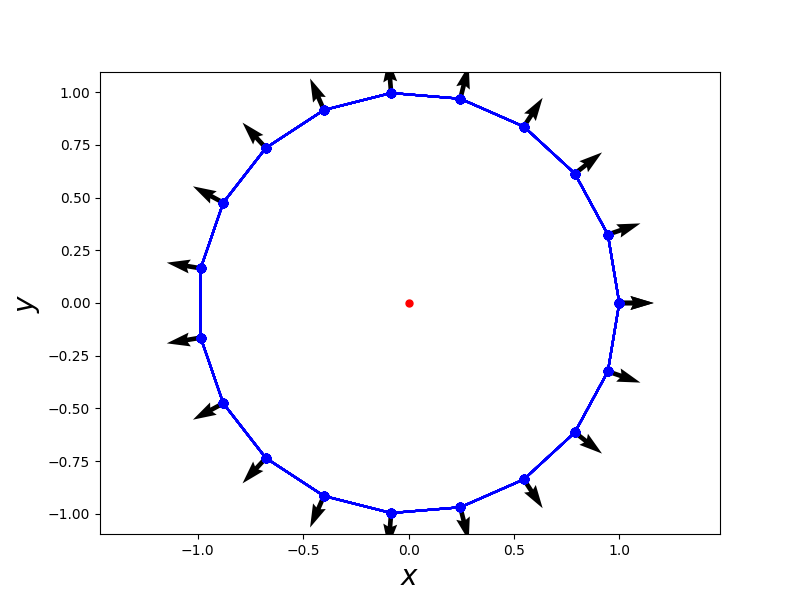
  4. 點電荷沿著圓週的電場

    5.  前個範例看起來好像太簡單了，沒有必要使用向量和zip()來處理，在下面這個問題中我們要沿著一個圓週，來計算電場的方向和大小。在這個情況下向量絕對是必要的，因為x方向跟y方向的分量都不會為0，所以必須用向量來考慮電場的各分量，如何隨著圓週上不同地點而改變。除此之外，這個程式中我們加入兩個過去沒有學過的元素。第一個就是要如何在一個程式中定義兩個繪圖物件(fig1,filg2)，並且用對應的軸(ax1,ax2)畫圖，最後再用繪圖物件來儲存不同的圖檔(fig1.savefig(),fig2.savefig())。另外一個應用是關於如何在螢幕上整齊的列印出我們的數據，包括位置向量、電場向量、電場的大小等等。我們希望數據的輸出是有格式化的，方便我們判斷輸出的結果是否與我們的物理上的預期相符合，以便檢驗我們的程式是否正確。例如在前面的範例程式當中，其輸出數據不格式化，就不方便我們來做檢驗。因為要列印的數據的數量很大，所以必須用系統化的整批作業方式，才能夠節省我們寫程式的時間。為了達到這個目的，我們先把要列印的數據收集在一個列表(list)當中，然後再把這個列表轉換為元組(tuple)就可以進行格式化的列印。 
    import matplotlib
matplotlib.use("Agg")
import matplotlib.pyplot as plt
import numpy as np

sin=np.sin; cos=np.cos; pi=np.pi
def EF_point(q,rq,r):
    ke=1.
    rrq=r-rq
    rrq0=np.linalg.norm(rrq)
    Es=ke*q/rrq0**2
    E=ke*q*rrq/rrq0**3
    return E,Es
q=1.
rq=np.array([0.,0.,0.])
t=np.linspace(0.,2.*pi,20)
rx=cos(t); ry=sin(t); rz=np.zeros_like(rx)
s8='%7.3f'*8
fig1, ax1 = plt.subplots(figsize=(8, 6))
fig2, ax2 = plt.subplots(figsize=(8, 6))
ax2.axis("equal")
for t1,x,y,z in zip(t,rx,ry,rz):
    r=np.array([x,y,z])
    Ev,Es=EF_point(q,rq,r)
    b1=[t1]; b1.extend(r); b1.extend(Ev);
    b1.append(Es)
    aa=tuple(b1)
    print((s8 %aa))
    ax1.plot(t1,Es,'k-x', ms=5)
    ax1.plot(t1,Ev[0],'r-o')
    ax1.plot(t1,Ev[1],'b-s')
    ax2.plot(rx,ry,'b-o')
    ax2.quiver(x,y,Ev[0],Ev[1],color='k')
ax1.set_xlabel(r"$\phi$", fontsize=20)
ax1.set_ylabel(r"$E_x,E_y,|E|$",fontsize=20)
ax2.set_xlabel(r"$x$", fontsize=20)
ax2.set_ylabel(r"$y$", fontsize=20)
ax2.plot(0,0,'ro', ms=5)
fig1.savefig("EF-04-A.png")
fig2.savefig("EF-04-B.png")
print('plot is done.')

    ============輸出:=============

    

      0.000  1.000  0.000  0.000  1.000  0.000  0.000  1.000
  0.331  0.946  0.325  0.000  0.946  0.325  0.000  1.000
  0.661  0.789  0.614  0.000  0.789  0.614  0.000  1.000
  0.992  0.547  0.837  0.000  0.547  0.837  0.000  1.000
  1.323  0.245  0.969  0.000  0.245  0.969  0.000  1.000
  1.653 -0.083  0.997  0.000 -0.083  0.997  0.000  1.000
  1.984 -0.402  0.916  0.000 -0.402  0.916  0.000  1.000
  2.315 -0.677  0.736  0.000 -0.677  0.736  0.000  1.000
  2.646 -0.879  0.476  0.000 -0.879  0.476  0.000  1.000
  2.976 -0.986  0.165  0.000 -0.986  0.165  0.000  1.000
  3.307 -0.986 -0.165  0.000 -0.986 -0.165  0.000  1.000
  3.638 -0.879 -0.476  0.000 -0.879 -0.476  0.000  1.000
  3.968 -0.677 -0.736  0.000 -0.677 -0.736  0.000  1.000
  4.299 -0.402 -0.916  0.000 -0.402 -0.916  0.000  1.000
  4.630 -0.083 -0.997  0.000 -0.083 -0.997  0.000  1.000
  4.960  0.245 -0.969  0.000  0.245 -0.969  0.000  1.000
  5.291  0.547 -0.837  0.000  0.547 -0.837  0.000  1.000
  5.622  0.789 -0.614  0.000  0.789 -0.614  0.000  1.000
  5.952  0.946 -0.325  0.000  0.946 -0.325  0.000  1.000
  6.283  1.000 -0.000  0.000  1.000 -0.000  0.000  1.000
plot is done.



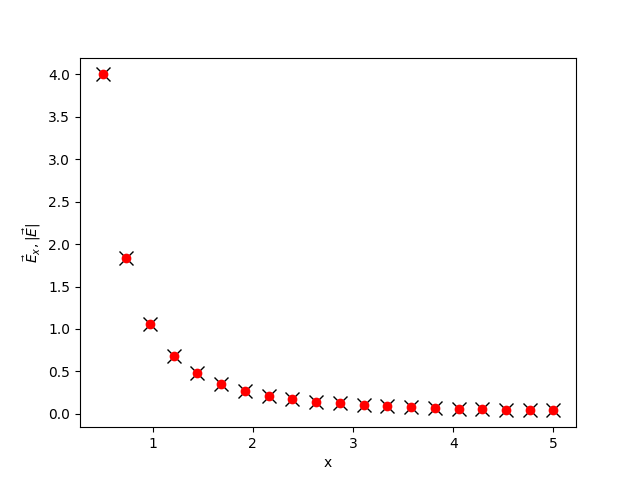
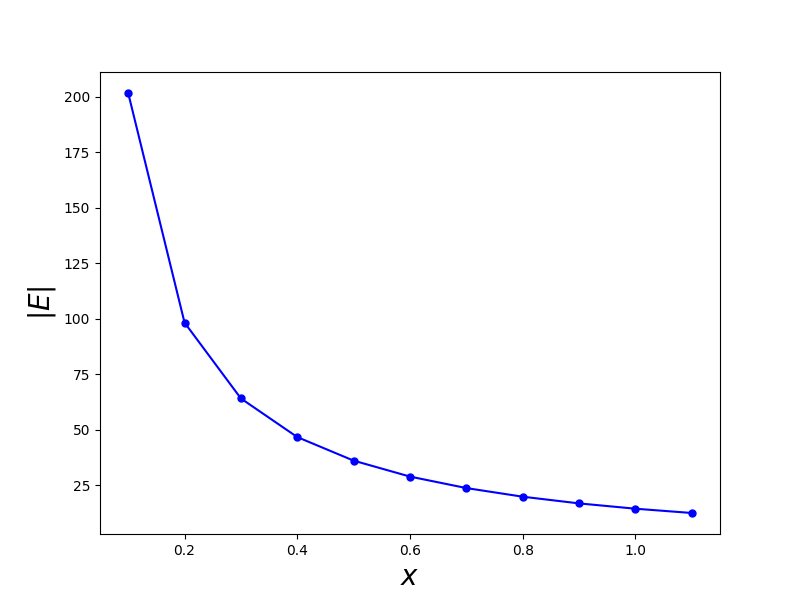
  5. 長直電線的電場

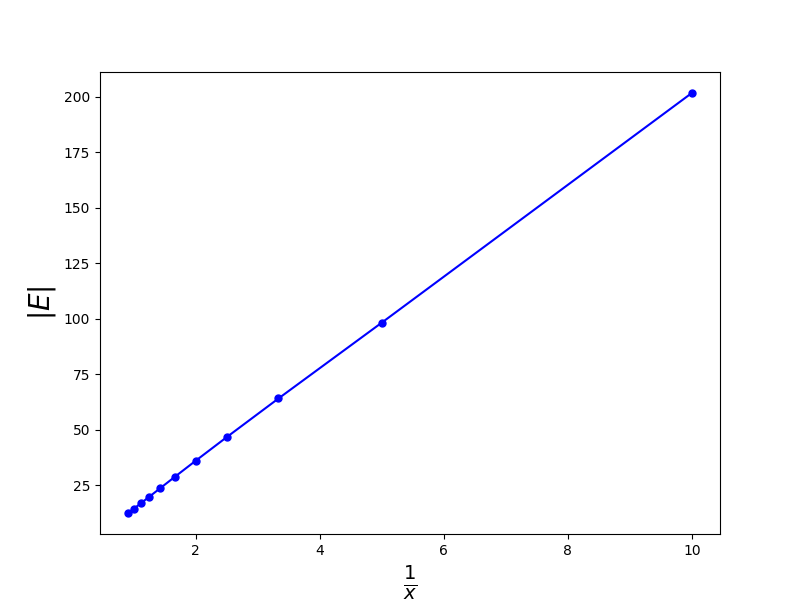
    6.  在這個範例程式中我們用21個電荷排成一條直線，然後計算這些電荷產生的電場沿著+x軸方向的變化。我們知道在這個情況下電場應該會跟距離的1次方成反比，而不是單一點電荷與距離平方成反比的函數行為。 
    import matplotlib
matplotlib.use("Agg")
import matplotlib.pyplot as plt
import numpy as np
sin=np.sin; cos=np.cos; pi=np.pi
def EF_points(Nq,q,rq,r):
    ke=1.
    E=np.zeros(3)
    for i in range(Nq):
        rrq=r-rq[i]
        rrq0=np.linalg.norm(rrq)
        E=E+ke*q[i]*rrq/rrq0**3
    Es=np.linalg.norm(E)
    return E,Es
Nq=21
q=[1. for i in range(Nq)]
rq=[0 for i in range(Nq)]
zq=np.linspace(-1,1,Nq)
for i in range(Nq):
    rq[i]=np.array([0.,0.,zq[i]])
t=np.linspace(0.1,1.1,11)
rx=t; rxi=1/rx
ry=np.zeros_like(rx); rz=np.zeros_like(rx)
fig1, ax1 = plt.subplots(figsize=(8, 6))
fig2, ax2 = plt.subplots(figsize=(8, 6))
s8='%9.3f'*8
aEs=[];aEv=[]
for x,y,z,xi in zip(rx,ry,rz,rxi):
    r=np.array([x,y,z])
    Ev,Es=EF_points(Nq,q,rq,r)
    aEs.append(Es); aEv.append(Ev)
    b1=[xi]; b1.extend(r); b1.extend(Ev);
    b1.append(Es)
    print((s8 %tuple(b1)))
ax1.plot(rx,aEs,'b-o', ms=5)
ax2.plot(rxi,aEs,'b-o', ms=5)
ax1.set_xlabel(r"$x$", fontsize=20)
ax1.set_ylabel(r"$|E|$", fontsize=20)
ax2.set_xlabel(r"$\frac{1}{x}$", fontsize=20)
ax2.set_ylabel(r"$|E|$", fontsize=20)
fig1.savefig("EF-06-A.png")
fig2.savefig("EF-06-B.png")
print('plot is done.')

    ============輸出:=============

    

       10.000    0.100    0.000    0.000  201.588    0.000    0.000  201.588
    5.000    0.200    0.000    0.000   98.241    0.000    0.000   98.241
    3.333    0.300    0.000    0.000   64.107    0.000   -0.000   64.107
    2.500    0.400    0.000    0.000   46.730    0.000   -0.000   46.730
    2.000    0.500    0.000    0.000   36.121    0.000    0.000   36.121
    1.667    0.600    0.000    0.000   28.948    0.000   -0.000   28.948
    1.429    0.700    0.000    0.000   23.779    0.000   -0.000   23.779
    1.250    0.800    0.000    0.000   19.891    0.000   -0.000   19.891
    1.111    0.900    0.000    0.000   16.877    0.000    0.000   16.877
    1.000    1.000    0.000    0.000   14.487    0.000   -0.000   14.487
    0.909    1.100    0.000    0.000   12.558    0.000   -0.000   12.558
plot is done.



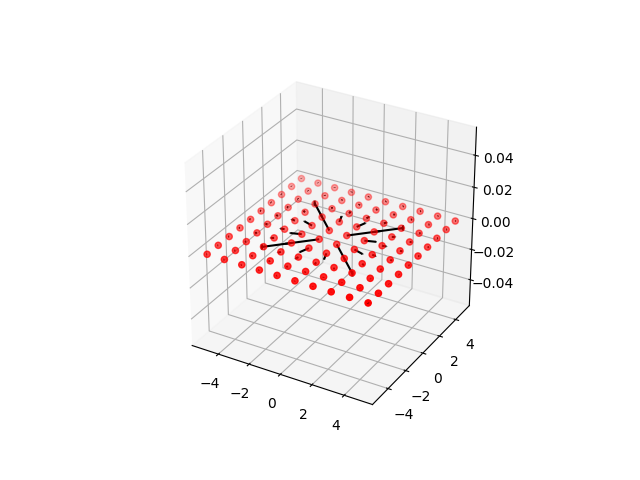
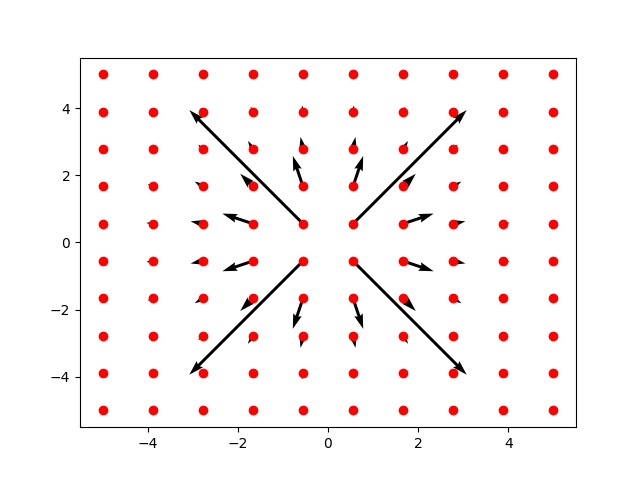
  6. 點電荷在XY平面上的電場

    7.  這個程式我們又再度計算單一點電荷的電場，但是在這個計算中我們並不是沿著某一個直線或者曲線來計算電場，而是結合了meshgrid的方法來，把平XY平面上做了11x11的格子點，針對這些點都計算出電場再把電場的箭頭向量畫上來。程式中我們畫了兩種圖，分別是二維平面和三維空間的向量圖。請注意在繪製2維圖之前，我們又新開了新的fig的視窗(fig = plt.figure())，這樣才能夠再重新的繪製一個獨立的圖框，最後就能再另存一個新圖檔(plt.savefig("E01q.png"))。 
    import matplotlib
matplotlib.use("Agg")
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np

fig = plt.figure()
ax = fig.gca(projection='3d')
ax.set_aspect("equal")
sin=np.sin; cos=np.cos; pi=np.pi
def EF_point(q,rq,r):
    ke=1.
    rrq=r-rq
    rrq0=np.linalg.norm(rrq)
    E=ke*q*rrq/rrq0**3
    return E
q=1.
rq=np.array([0.,0.,0.])
N=10
x=np.linspace(-5,5,N)
y=np.linspace(-5,5,N)
X,Y=np.meshgrid(x,y)
Z=np.zeros_like(X)
ax.scatter(X,Y,Z, color='r')
U=[]; V=[]; W=[]
for x1,y1,z1 in zip(X,Y,Z):
    for x2,y2,z2 in zip(x1,y1,z1):
        r=np.array([x2,y2,z2])
        ER=EF_point(q,rq,r)
        U.append(ER[0]);V.append(ER[1]);W.append(ER[2]);
        ax.quiver(x2, y2, z2, ER[0], ER[1], ER[2],
        pivot = 'tail', length=2.0, color='k', arrow_length_ratio = 0.002)
plt.savefig("E01.png")

fig = plt.figure()
plt.plot(X,Y,'ro')
plt.quiver(X,Y,U,V,scale=5)
plt.savefig("E01q.png")
print ('plot is done')

作業

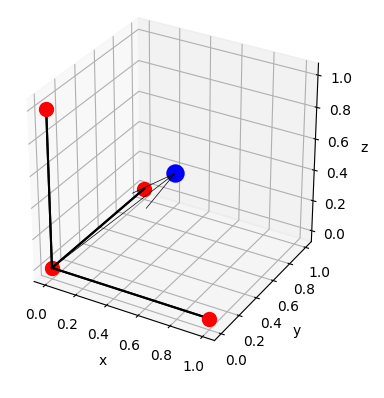
1. HW-3-1: 下面的樣本程式可以畫出三維空間的4個點，並且把這4個點用線段連通。請你利用這個樣本程式加以修改，使能夠畫出下面所附的立方體的圖形。
HW3-1的參考程式如下： 
import matplotlib
matplotlib.use("Agg")
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np

fig = plt.figure()
ax = fig.gca(projection='3d')
ax.set_aspect("equal")
L=[[0,0,0],[1,0,0],[0,1,0],[0,0,1]]
for i in L:
    ax.scatter(i[0],i[1],i[2],c='r', marker='o', s=100)
A=np.array(L)
for i in A:
    for j in A:
        d=np.linalg.norm(i-j)
        if(0.1 < d < 1.1):
            ax.plot([i[0],j[0]],[i[1],j[1]],[i[2],j[2]], color='k')
ax.scatter(0.5,0.5,0.5,c='b', marker='o', s=150)
ax.quiver(0,0,0,0.5,0.5,0.5, linewidth=0.5, color='k')
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_zlabel("z")
plt.savefig("4points.png")
print('plot is done.')


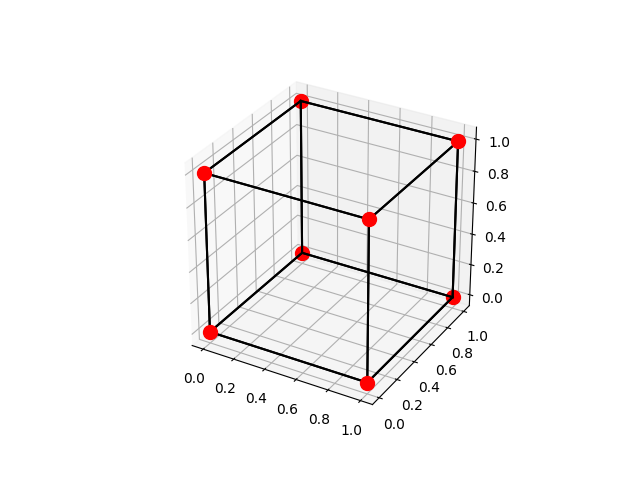
HW-3-2：
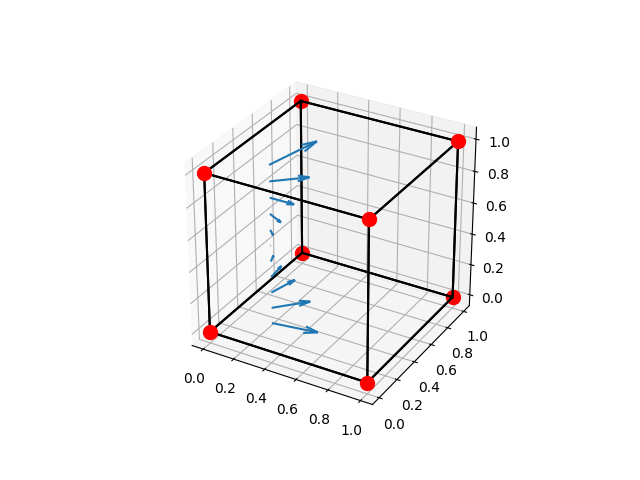
下面的作業是要各位同學在前一個立方體的問題當中在頂角放上一個電荷，電荷量q=1，然後計算x=0.25, y=0.25, z=0,0.1,0.2,0.3 ... 1共11個點的電場(也就是x,y固定為0.25，沿著向+z軸的方向，向上延伸11個點)，並且將這個電場的大小對z作圖，也同時在3D的立方體當中沿著+z的方向的11個點，畫出電場的箭頭。下面所提供的程式可以幫助你建立基本的架構，請你再花一些心思加以修改，以其能夠完成這個作業。也許有一點困難，同學們如果需要幫忙可以用email跟我聯絡。
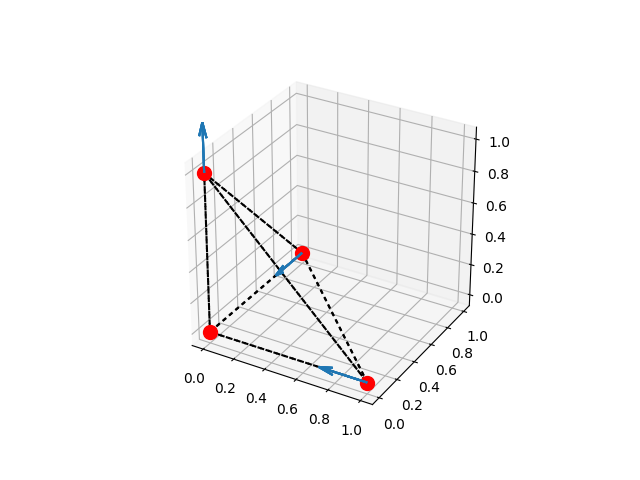
HW-3-2參考程式如下： 
import matplotlib
matplotlib.use("Agg")
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np

fig1 = plt.figure()
ax1 = fig1.gca(projection='3d')
fig2, ax2 = plt.subplots(figsize=(8, 6))
ax1.set_aspect("equal")
L=[[0,0,0],[1,0,0],[0,1,0],[0,0,1]]
for i in L:
    ax1.scatter(i[0],i[1],i[2],c='r', marker='o', s=100)
A=np.array(L)
for i in A:
    for j in A:
        d=np.linalg.norm(i-j)
        ax1.plot([i[0],j[0]],[i[1],j[1]],[i[2],j[2]], dashes=[2, 2],color='k')
        ax1.quiver(i[0],i[1],i[2],-i[0],-i[1],i[2], length=0.3)
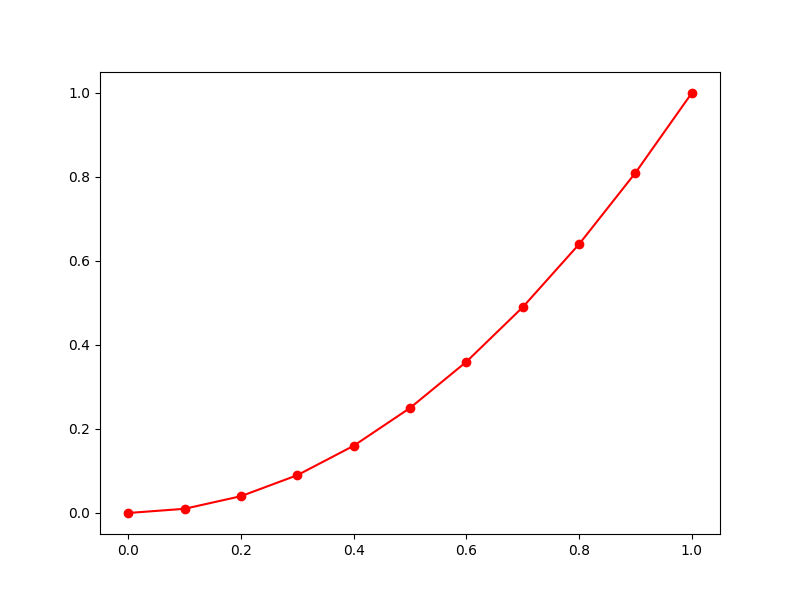
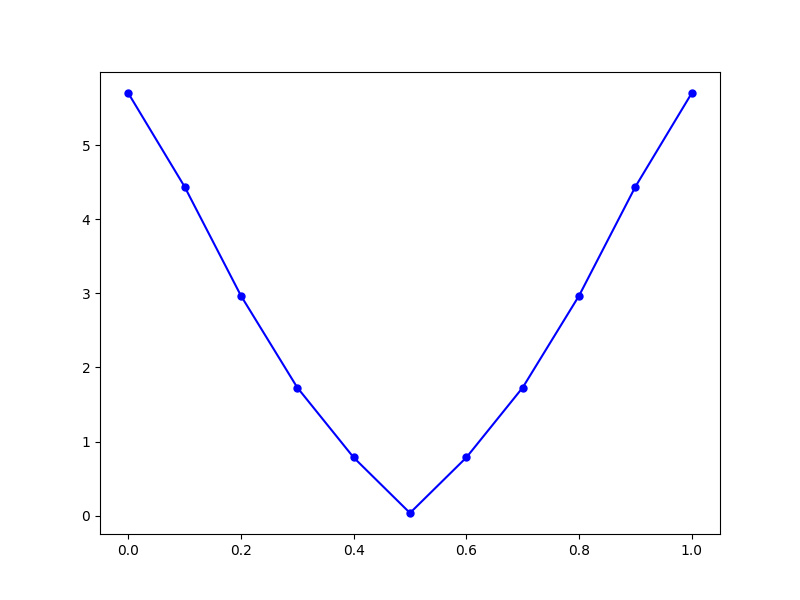
x=np.linspace(0,1,11)
y=x**2
ax2.plot(x,y,'r-o')
fig1.savefig("HW-3-2-RA.png")
fig2.savefig("HW-3-2-RB.png")
print('plot is done.')