電場電通量

電通量

電荷的周圍充斥著電場。若以圖形表示，該電場可以被表示為從一個點（電荷）散開的輻射線，稱為電場線或電力線。而這些線的密度與電場強度呈正相關，稱為電通量密度，也就是每單位面積的電力線數目。因此，電通量與穿過表面的電場線的總數成正比。為了簡化計算，通常在計算上會選取垂直於電力線的表面。如果電場為一均勻電場，則通過所選面積 \( \mathbf {S} \) 的表面的通量為 \[ \Phi_{E}=\mathbf{E} \cdot \mathbf{S} =ES \cos \theta \] 其中\( \mathbf{E} \)為電場（單位為 V/m ）、\(E\)為電場強度、 \(S\) 為表面面積、 \( \theta\) 為電場線與 \(S\) 的法線之間的夾角。

電通量的大小與電場的強度成正比
電通量的大小與表面積的大小成正比
電通量的大小與電場和面的法線夾角有關

如果電場為一非均勻電場，則通常會將此一較大面積的電通量分割，改取一小塊面積 \( d\mathbf{S}\) 上的電通量 \(d\Phi_{E}\) \[ d\Phi_{E}=\mathbf{E} \cdot d\mathbf{S}\] （電場 \(\mathbf {E}\)乘以垂直於所選面積表面的分量）。因此，表面 \(S\) 上的電通量可由表面積分得到：
\(\Phi_{E}=\iint_{S} \mathbf{E} \cdot d\mathbf{S}\)
其中 \(\mathbf{E}\)是電場，\(d\mathbf{S}\)是閉合表面\(S\)上的微小面積，其方向定義為表面法線朝外。
根據高斯定律，通過任一封閉曲面（高斯面）的淨電通量(\(\Phi_{E}\))，必與該封閉曲面內所圍之淨電荷量(\( Q_{\rm{enc}}\))成正比。而在真空中，此比例常數為一定值\( 1/\varepsilon_{0}\)。其數學式為 :
\(\Phi_{E}=\oint_{\scriptstyle{S}} \mathbf{E} \cdot d\mathbf{S} =\frac{Q_{\rm{enc}}}{\varepsilon_{0}} \)
其中 \(\mathbf{E}\)是電場、 \(S\) 是任一封閉曲面、 \( Q_{\rm {enc}}\) 是曲面 \(S\) 內的總淨電荷。\(\varepsilon_{0}\)是介電常數（為一通用常數，也稱為真空中電容率或真空介電常數）。\( \varepsilon _{0}\approx 8.854187817...\times 10^{-12}\) (F/m) 此一關係式以其積分形式被稱為電場高斯定律，是四個馬克士威方程式之一。電通量的單位為伏特米（V·m）。

1.畫出平面的方塊為電通量的計算做準備

\(-R \le x \le R; \,\,\, -R \le z \le R; L=2R; R=1; 面積A=L^2=4\)

GlowScript 3.2 VPython
scene=canvas(width=800, height=600, center=vector(0.1,0.3,0), forward=vec(0,-0.2,-1))
X=arrow(pos=vec(0,0,0),axis=vec(1.2,0,0),shaftwidth=0.02,headwidth=0.04,color=vec(1,0,0))
Y=arrow(pos=vec(0,0,0),axis=vec(0,0.5,0),shaftwidth=0.02,headwidth=0.04,color=vec(0,1,0))
Z=arrow(pos=vec(0,0,0),axis=vec(0,0,1.2),shaftwidth=0.02,headwidth=0.04,color=vec(0,0,1))
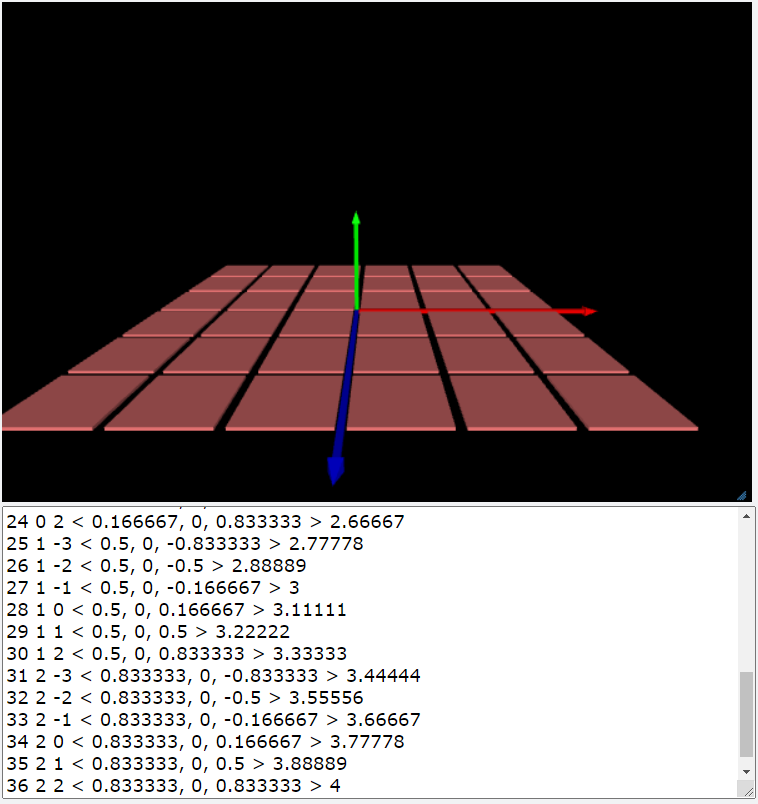
R=1; N=3; dx=R/N; dz=dx
A=0; E=vec(1,1,0); FLUX=0; n=vec(0,1,0)
for i in range(-N,N):
    x=dx*(i+0.5)
    for j in range(-N,N):
        z=dz*(j+0.5)
        print(i,j,vec(x,0,z))
        box(pos=vec(x,0,z),size=vec(dx*0.9,0.01,dz*0.9),color=vec(1,0.5,0.5))
        A+=dx*dz        
        FLUX+=dot(E,n)
        arrow(pos=vec(x,0,z),axis=E*0.1,shaftwidth=0.01,headwidth=0.02,color=vec(1,1,0))
        arrow(pos=vec(x,0,z),axis=n*0.1,shaftwidth=0.01,headwidth=0.02,color=vec(0,1,1))
print(N,'A=',A,'  FLUX=',FLUX)

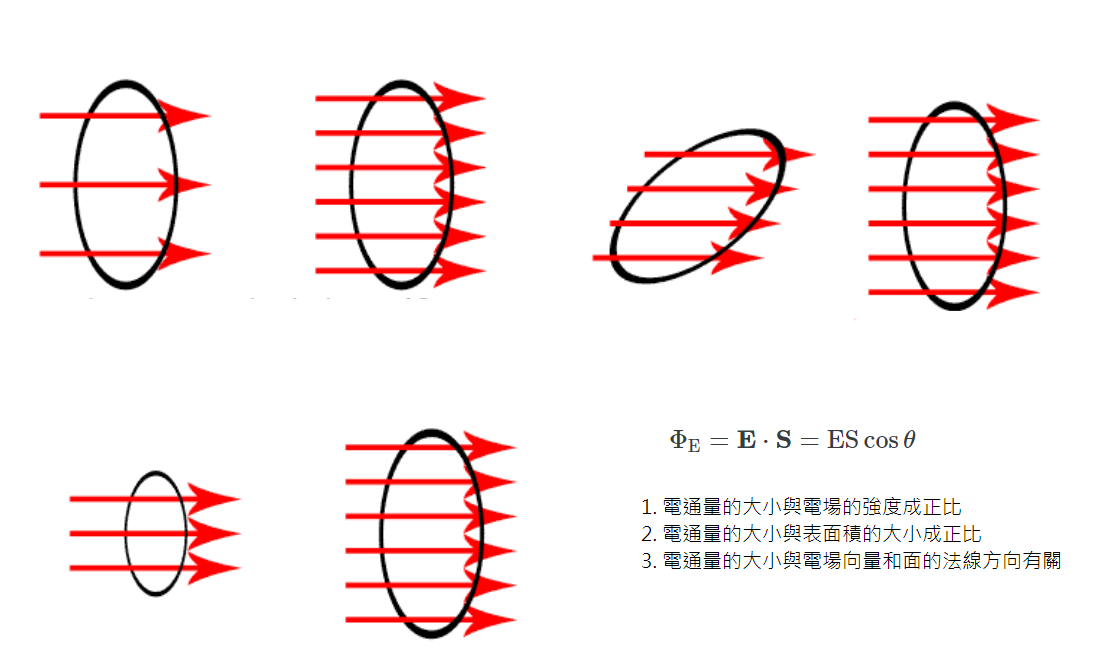
glowscript:畫出平面的方塊為電通量的計算做準備(PS-EFlux-01.py)

2.計算均勻電場的電通量

\(-R \le x \le R; \,\,\, -R \le z \le R; L=2R; R=1; A=L^2=4\)
\(均勻電場\vec{E_0}=(1,0,1), \,\, xz-平面的法線\hat{n}=(0,1,0)\)
\(電通量=\vec{E_0} \cdot \hat{n} A\)

GlowScript 3.2 VPython
scene=canvas(width=800, height=600, center=vector(0.1,0.3,0), forward=vec(0,-0.2,-1))
X=arrow(pos=vec(0,0,0),axis=vec(1.2,0,0),shaftwidth=0.02,headwidth=0.04,color=vec(1,0,0))
Y=arrow(pos=vec(0,0,0),axis=vec(0,0.5,0),shaftwidth=0.02,headwidth=0.04,color=vec(0,1,0))
Z=arrow(pos=vec(0,0,0),axis=vec(0,0,1.2),shaftwidth=0.02,headwidth=0.04,color=vec(0,0,1))
R=1; N=3; dx=R/N; dz=dx
A=0; E=vec(1,1,0); FLUX=0; n=vec(0,1,0)
for i in range(-N,N):
    x=dx*(i+0.5)
    for j in range(-N,N):
        z=dz*(j+0.5)
        #print(i,j,vec(x,0,z))
        box(pos=vec(x,0,z),size=vec(dx*0.9,0.01,dz*0.9),color=vec(1,0.5,0.5))
        A+=dx*dz        
        FLUX+=dot(E,n)*dx*dz
        arrow(pos=vec(x,0,z),axis=E*0.1,shaftwidth=0.01,headwidth=0.02,color=vec(1,1,0))
        arrow(pos=vec(x,0,z),axis=n*0.1,shaftwidth=0.01,headwidth=0.02,color=vec(0,1,1))
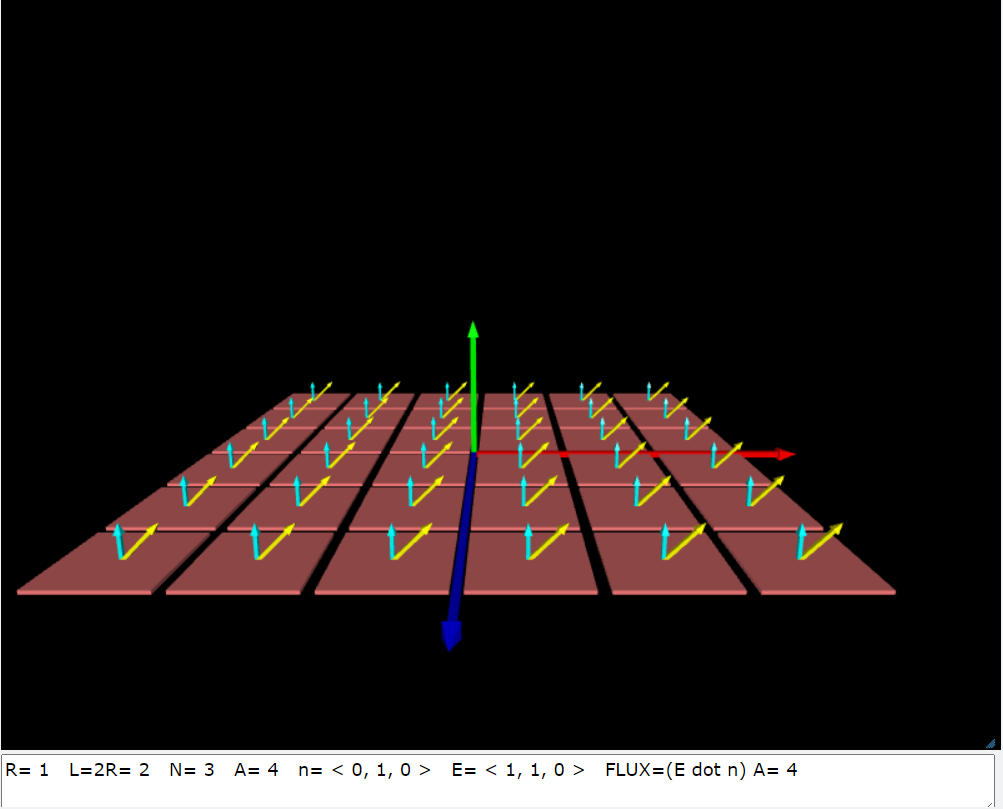
print('R=',R,'  L=2R=',2*R,'  N=',N,'  A=',A,'  n=',n,'  E=',E,'  FLUX=(E dot n) A=',FLUX)

glowscript:計算均勻電場的電通量(PS-EFlux-02.py)

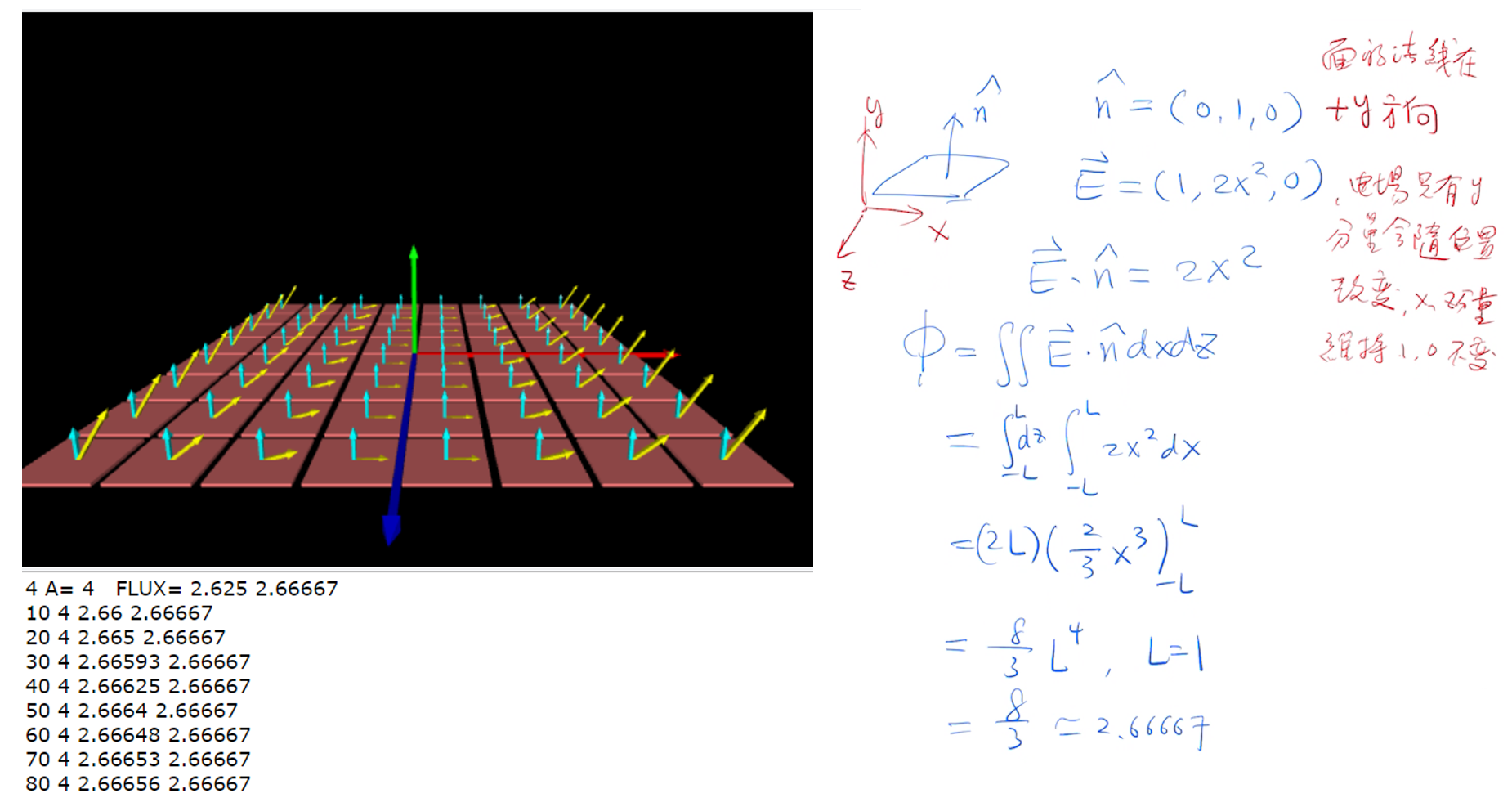
3.計算不均勻電場的電通量

\(-R \le x \le R; \,\,\, -R \le z \le R; L=2R; R=1; A=L^2=4\)
\(不均勻電場\vec{E}=(1,2x^2,0), \,\, xz-平面的法線\hat{n}=(0,1,0)\)
\(電通量=\int_{-R}^{R} \int_{-R}^{R} \vec{E} \cdot \hat{n} \,dx dz=\dfrac{8}{3}\simeq 2.6667\)

GlowScript 3.2 VPython
scene=canvas(width=600, height=400, center=vector(0.1,0.3,0), forward=vec(0,-0.2,-1))
X=arrow(pos=vec(0,0,0),axis=vec(1.2,0,0),shaftwidth=0.02,headwidth=0.04,color=vec(1,0,0))
Y=arrow(pos=vec(0,0,0),axis=vec(0,0.5,0),shaftwidth=0.02,headwidth=0.04,color=vec(0,1,0))
Z=arrow(pos=vec(0,0,0),axis=vec(0,0,1.2),shaftwidth=0.02,headwidth=0.04,color=vec(0,0,1))
R=1; N=4; dx=R/N; dz=dx
A=0; E=vec(1,1,0); FLUX=0; n=vec(0,1,0)
for i in range(-N,N):
    x=dx*(i+0.5)
    for j in range(-N,N):
        z=dz*(j+0.5)
        r=vec(x,0,z)
        box(pos=r,size=vec(dx*0.9,0.01,dz*0.9),color=vec(1,0.5,0.5))
        A+=dx*dz 
        E=vec(1,2*x**2,0)
        #if(j==-N): print(i,j,r,E)
        FLUX+=dot(E,n)*dx*dz
        arrow(pos=vec(x,0,z),axis=E*0.1,shaftwidth=0.01,headwidth=0.02,color=vec(1,1,0))
        arrow(pos=vec(x,0,z),axis=n*0.1,shaftwidth=0.01,headwidth=0.02,color=vec(0,1,1))
print(N,'A=',A,'  FLUX=',FLUX,8/3)

glowscript:計算不均勻電場的電通量(PS-EFlux-03.py)

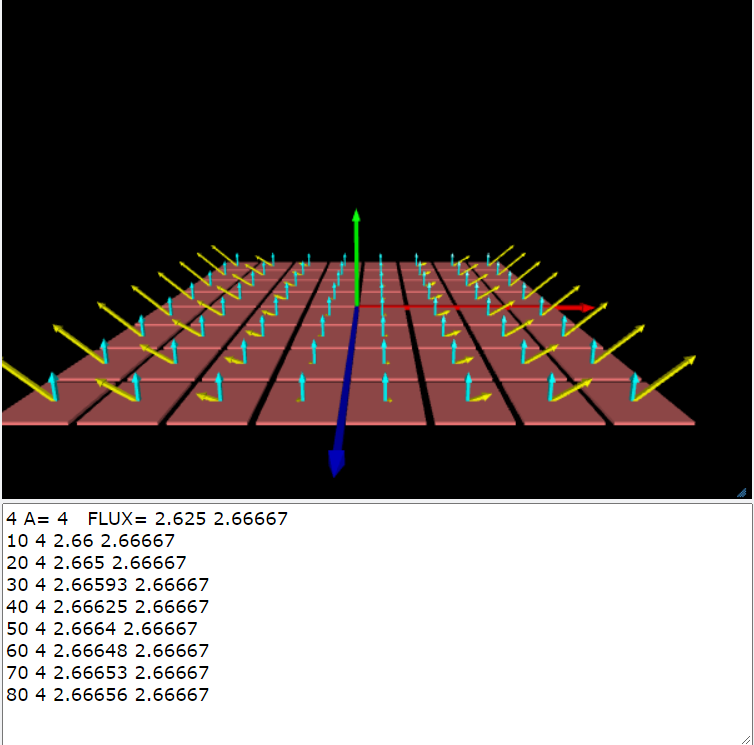
4.用函數計算電通量

\(-R \le x \le R; \,\,\, -R \le z \le R; L=2R; R=1; A=L^2=4\)
\(不均勻電場\vec{E}=(2x,2x^2,0), \,\, xz-平面的法線\hat{n}=(0,1,0)\)
\(電通量=\int_{-R}^{R} \int_{-R}^{R} \vec{E} \cdot \hat{n} \,dx dz=\dfrac{8}{3}\simeq 2.6667\)
將電通量的計算寫成一個函數就可以反覆的呼叫這個函數，比較不同的切割數量\(N\)所得到的電通量值，就可以估計電通量的精確值。
雖然電場的x分量隨著位置改變\(E_x=2x\)，但是法線方向仍然在+y方向\(\hat{n}=(0,1,0)\)，所以電場的x方向分量對電通量並沒有貢獻，因此電通量的結果仍然與上一個題目所得的電動量相等都是\(8/3\)。

GlowScript 3.2 VPython
scene=canvas(width=600, height=400, center=vector(0.1,0.3,0), forward=vec(0,-0.2,-1))
X=arrow(pos=vec(0,0,0),axis=vec(1.2,0,0),shaftwidth=0.02,headwidth=0.04,color=vec(1,0,0))
Y=arrow(pos=vec(0,0,0),axis=vec(0,0.5,0),shaftwidth=0.02,headwidth=0.04,color=vec(0,1,0))
Z=arrow(pos=vec(0,0,0),axis=vec(0,0,1.2),shaftwidth=0.02,headwidth=0.04,color=vec(0,0,1))
R=1; N=4; dx=R/N; dz=dx
A=0; E=vec(1,1,0); FLUX=0; n=vec(0,1,0)
for i in range(-N,N):
    x=dx*(i+0.5)
    for j in range(-N,N):
        z=dz*(j+0.5)
        r=vec(x,0,z)
        box(pos=r,size=vec(dx*0.9,0.01,dz*0.9),color=vec(1,0.5,0.5))
        A+=dx*dz 
        E=vec(2*x,2*x**2,0)
        FLUX+=dot(E,n)*dx*dz
        arrow(pos=vec(x,0,z),axis=E*0.1,shaftwidth=0.01,headwidth=0.02,color=vec(1,1,0))
        arrow(pos=vec(x,0,z),axis=n*0.1,shaftwidth=0.01,headwidth=0.02,color=vec(0,1,1))
print(N,'A=',A,'  FLUX=',FLUX,8/3)

def FLUXSQ(N):
    R=1; dx=R/N; dz=dx
    A=0; E=vec(1,1,0); FLUX=0; n=vec(0,1,0)
    for i in range(-N,N):
        x=dx*(i+0.5)
        for j in range(-N,N):
            z=dz*(j+0.5)
            r=vec(x,0,z)
            A+=dx*dz 
            E=vec(2*x,2*x**2,0)
            FLUX+=dot(E,n)*dx*dz
    return A,FLUX

for j in range(8):
    N=10+10*j
    A,F=FLUXSQ(N)
    print(N,A,F,8/3)

glowscript:用函數計算電通量(PS-EFlux-04.py)

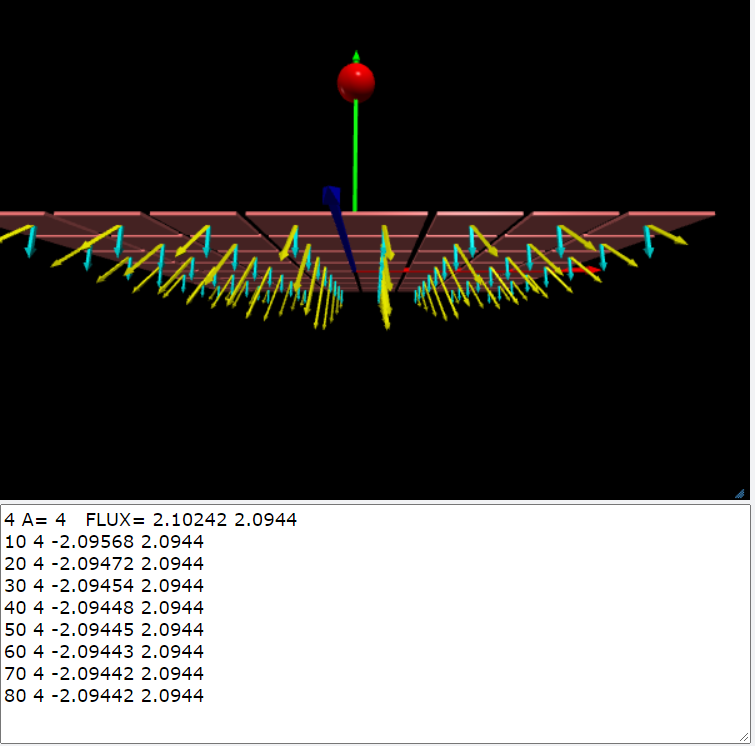
5.計算點電荷的電通量

\(-R \le x \le R; \,\,\, -R \le z \le R; L=2R; R=1; A=L^2=4\)
\(點電荷的電場\vec{E}=k q_1 / |\vec{r}-\vec{r_q}|^3 (\vec{r}-\vec{r_q}), \,\, xz-平面的法線\hat{n}=(0,1,0)\)
\(電通量=\int_{-R}^{R} \int_{-R}^{R} \vec{E} \cdot \hat{n} \,dx dz=\dfrac{4 \pi}{6}\simeq 2.0944\)

GlowScript 3.2 VPython
scene=canvas(width=600, height=400, center=vector(0.1,0.1,0), forward=vec(0,0.2,-1))
X=arrow(pos=vec(0,0,0),axis=vec(1.2,0,0),shaftwidth=0.02,headwidth=0.04,color=vec(1,0,0))
Y=arrow(pos=vec(0,0,0),axis=vec(0,1.2,0),shaftwidth=0.02,headwidth=0.04,color=vec(0,1,0))
Z=arrow(pos=vec(0,0,0),axis=vec(0,0,1.2),shaftwidth=0.02,headwidth=0.04,color=vec(0,0,1))
R=1; N=4; dx=R/N; dz=dx
q1=1.; rq1=vec(0,R,0.); k=1
Q1=sphere(pos=rq1,radius=0.1,color=vec(1,0,0))
A=0; FLUX=0; n=vec(0,-1,0)
for i in range(-N,N):
    x=dx*(i+0.5)
    for j in range(-N,N):
        z=dz*(j+0.5)
        r=vec(x,0,z)
        box(pos=r,size=vec(dx*0.9,0.01,dz*0.9),color=vec(1,0.5,0.5))
        A+=dx*dz 
        E=k*q1/mag(r-rq1)**3*(r-rq1)
        FLUX+=dot(E,n)*dx*dz
        arrow(pos=vec(x,0,z),axis=E*0.3,shaftwidth=0.01,headwidth=0.02,color=vec(1,1,0))
        arrow(pos=vec(x,0,z),axis=n*0.1,shaftwidth=0.01,headwidth=0.02,color=vec(0,1,1))
print(N,'A=',A,'  FLUX=',FLUX,4*pi/6)

def FLUXSQ(N):
    R=1; dx=R/N; dz=dx
    A=0; E=vec(1,1,0); FLUX=0; n=vec(0,1,0)
    for i in range(-N,N):
        x=dx*(i+0.5)
        for j in range(-N,N):
            z=dz*(j+0.5)
            r=vec(x,0,z)
            A+=dx*dz 
            E=k*q1/mag(r-rq1)**3*(r-rq1)
            FLUX+=dot(E,n)*dx*dz
    return A,FLUX

for j in range(8):
    N=10+10*j
    A,F=FLUXSQ(N)
    print(N,A,F,4*pi/6)

glowscript:計算點電荷的電通量(PS-EFlux-05.py)

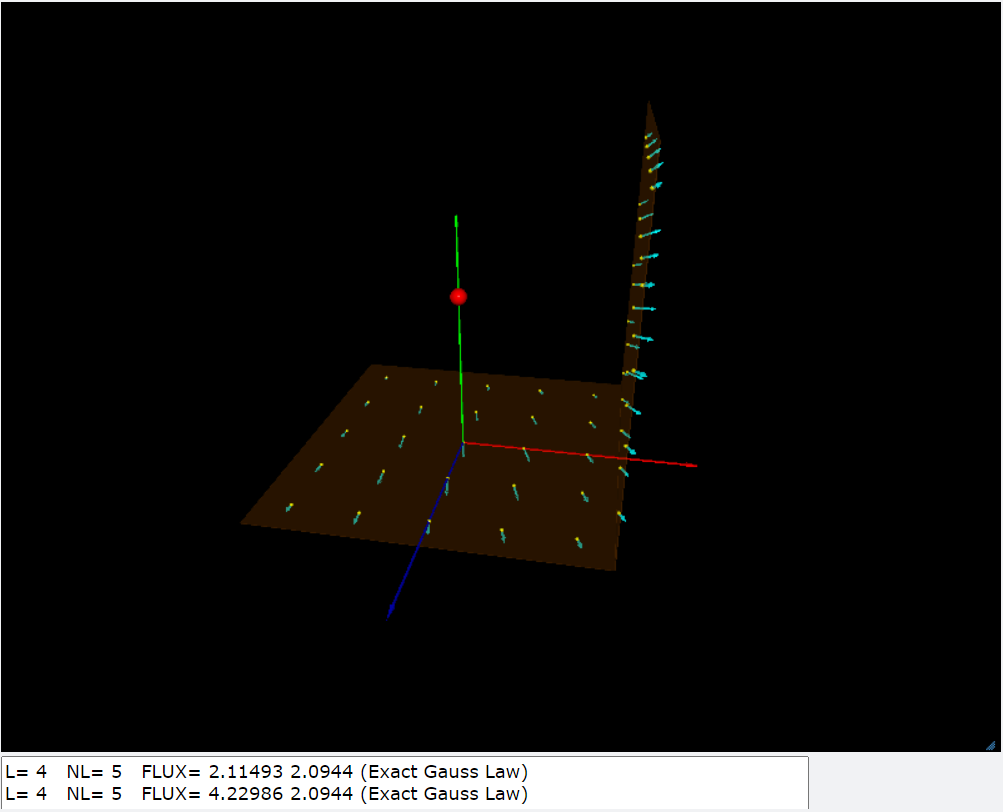
6.一個點電荷對兩個平面的電通量

GlowScript 3.2 VPython

def EF_point(q,rq,r):
    ke=1.; rrq=r-rq
    E=ke*q*rrq/mag(rrq)**3
    return E

L=4; NL=5; dx=L/NL; dz=L/NL; da=dx*dz
q1=1.; rq1=vec(0,L/2,0.)
scene=canvas(width=800, height=600, center=vec(0.5,L/4,0))
X=arrow(pos=vec(0,0,0),axis=vec(3,0,0),shaftwidth=0.02,headwidth=0.04,color=vec(1,0,0))
Y=arrow(pos=vec(0,0,0),axis=vec(0,3,0),shaftwidth=0.02,headwidth=0.04,color=vec(0,1,0))
Z=arrow(pos=vec(0,0,0),axis=vec(0,0,3),shaftwidth=0.02,headwidth=0.04,color=vec(0,0,1))
plane=box(pos=vec(0,0,0),size=vec(L,0.01,L),color=vec(1,0.5,0),opacity=0.2)
Q1=sphere(pos=rq1,radius=0.1,color=vec(1,0,0))

eflux=0
for i in range(NL):
    x=-L/2+dx*(i+0.5)
    for j in range(NL):
        z=-L/2+dz*(j+0.5)
        r=vec(x,0,z)
        E=EF_point(q1,rq1,r)
        n=vec(0,-1,0)
        sphere(pos=r,radius=0.02,color=vec(1,1,0))
        arrow(pos=r,axis=E,shaftwidth=0.02,headwidth=0.04,color=color.cyan)
        Eda=dot(E,n)*da
        eflux+=Eda
print('L=',L,'  NL=',NL,'  FLUX=',eflux,4*pi/6,'(Exact Gauss Law)')

plane=box(pos=vec(L/2,L/2,0),size=vec(0.01,L,L),color=vec(1,0.5,0),opacity=0.2)
for i in range(NL):
    y=0+dx*(i+0.5)
    for j in range(NL):
        z=-L/2+dz*(j+0.5)
        r=vec(L/2,y,z)
        E=EF_point(q1,rq1,r)
        n=vec(1,0,0)
        sphere(pos=r,radius=0.02,color=vec(1,1,0))
        arrow(pos=r,axis=E,shaftwidth=0.02,headwidth=0.04,color=color.cyan)
        Eda=dot(E,n)*da
        eflux+=Eda
print('L=',L,'  NL=',NL,'  FLUX=',eflux,4*pi/6,'(Exact Gauss Law)')

glowscript:一個點電荷對兩個平面的電通量(PS-EFlux-06.py)

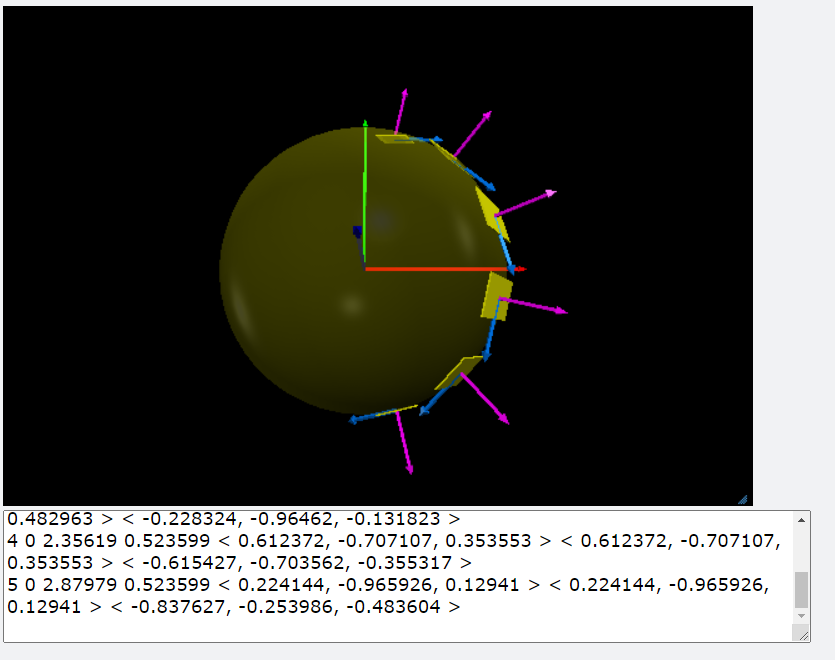
7.球座標

\(x=R \cos \phi \sin \theta; \,\, y=R \cos \theta; \,\, z=R \cos \theta \)

GlowScript 3.2 VPython
scene=canvas(width=600, height=400, center=vector(0.1,0.1,0), forward=vec(0,0.2,-1))
X=arrow(pos=vec(0,0,0),axis=vec(1.2,0,0),shaftwidth=0.02,headwidth=0.04,color=vec(1,0,0))
Y=arrow(pos=vec(0,0,0),axis=vec(0,1.2,0),shaftwidth=0.02,headwidth=0.04,color=vec(0,1,0))
Z=arrow(pos=vec(0,0,0),axis=vec(0,0,1.2),shaftwidth=0.02,headwidth=0.04,color=vec(0,0,1))
R=1; N=6; dt=pi/N; df=2*pi/N; w=0.1
sphere(pos=vec(0,0,0),radius=R,color=vec(1,1,0),opacity=0.2)
for i in range(N):
    t=dt*(i+0.5)
    for j in range(1):
        f=df*(j+0.5)
        r=vec(R*cos(f)*sin(t),R*cos(t),R*sin(f)*sin(t))
        n=hat(r)
        r1=vec(R*cos(f)*sin(t+0.01),R*cos(t+0.01),R*sin(f)*sin(t+0.01))
        tr=hat(r1-r)
        print(i,j,t,f,r,n,tr)
        box(pos=r,axis=tr,up=n,length=0.5*R*dt,width=0.5*R*sin(t)*df,height=0.01, color=vec(1,1,0))
        arrow(pos=r,axis=r*0.4,shaftwidth=0.02,headwidth=0.05,color=vec(1,0,1))
        arrow(pos=r,axis=tr*0.4,shaftwidth=0.02,headwidth=0.05,color=vec(0,0.5,1))

glowscript:球座標(PS-EFlux-07.py)

8.球面的面積與球的體積

\(A=4\pi R^2\)

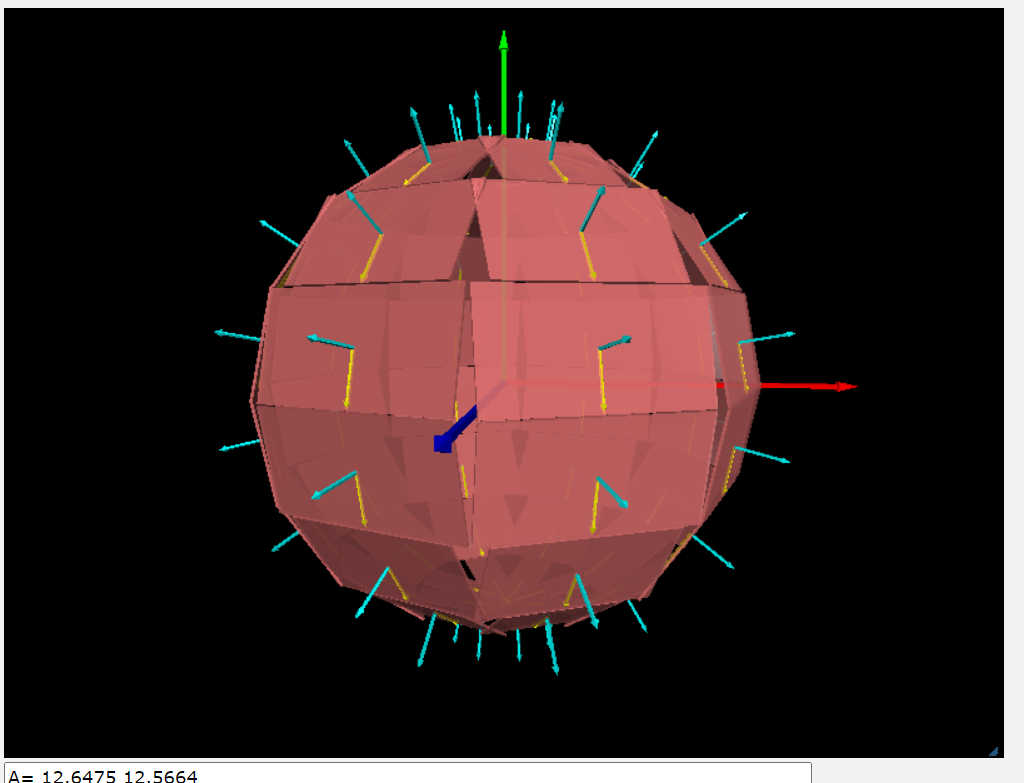
GlowScript 3.2 VPython
scene=canvas(width=800, height=600, center=vector(0.0,0.0,0), forward=vec(-0.1,-0.1,-1))
X=arrow(pos=vec(0,0,0),axis=vec(1.5,0,0),shaftwidth=0.02,headwidth=0.04,color=vec(1,0,0))
Y=arrow(pos=vec(0,0,0),axis=vec(0,1.5,0),shaftwidth=0.02,headwidth=0.04,color=vec(0,1,0))
Z=arrow(pos=vec(0,0,0),axis=vec(0,0,1.5),shaftwidth=0.02,headwidth=0.04,color=vec(0,0,1))
#------------------------for the surface of a sphere----------------
R=1; N=8; dt=pi/N; df=2*pi/N
A=0; 
for i in range(N):
    t=dt*(i+0.5)
    for j in range(N):
        f=df*(j+0.5)
        x=R*sin(t)*cos(f); z=R*sin(t)*sin(f); y=R*cos(t)
        r=vec(x,y,z)
        n=hat(r)
        r1=vec(R*sin(t+0.01)*cos(f),R*cos(t+0.01),R*sin(t+0.01)*sin(f))
        tv=hat(r1-r)
        b=box(pos=r,size=vec(R*dt,0.01,R*sin(t)*df),axis=tv,up=r,color=vec(1,0.5,0.5),opacity=0.7)
        arrow(pos=r,axis=b.axis*0.5,shaftwidth=0.01,headwidth=0.02,color=vec(1,1,0))
        arrow(pos=r,axis=n*0.2,shaftwidth=0.01,headwidth=0.02,color=vec(0,1,1))
        A+=R**2*sin(t)*dt*df
print('A=',A,4*pi*R**2)
#-----------------------for the volume of a sphere-------------
R1=1; N=100; dt=pi/N; df=2*pi/N; dR=R1/N; V=0
for k in range(N):
    R=dR*(k+0.5)
    for i in range(N):
        t=dt*(i+0.5)
        for j in range(N):
            f=df*(j+0.5)
            x=R*sin(t)*cos(f); z=R*sin(t)*sin(f); y=R*cos(t)
            r=vec(x,y,z)
            V+=R**2*sin(t)*dt*df*dR
print('V=',V,4/3*pi*R1**3)

glowscript:球面的面積與球的體積(PS-EFlux-08.py)

9.一個點電荷對半球面的電通量

在這個計算當中我們選取的高斯面是一個半徑為R的球面，座標的原點就設在球心上。因為我們把原點設在球的球心，因此每一個球面上的點的法向量就是位置向量。我們只要利用函數副程式(EF_points)計算出這個點的電場：點電荷q的座標\(\vec{r'}\), 欲計算的電場位置\(\vec{r}\), 電場(\(\vec{E}\))在置\(\vec{r}\)的向量： \[ \vec{E}(\vec{r})=\frac{kq}{r^3}\vec{r} \] 再將\(\vec{E}\)與位置向量\(\vec{r}\)取內積，很快可以把面積分算出來。三維空間裏，還有其他的座標系，例如圓柱座標係就是其中一種當。我們考慮我們的電荷呈線性分佈時，圓柱座標係就是一個比較好的選擇，因為這個時候的高斯面應該會是圓柱體的表面比較能夠符合電場問題的對稱性。程式中 dA=R*dt*R*sin(T)*df就是球座標系的面積微量元素：\(dA=R^2 \sin(\theta) d \theta d \phi\)。

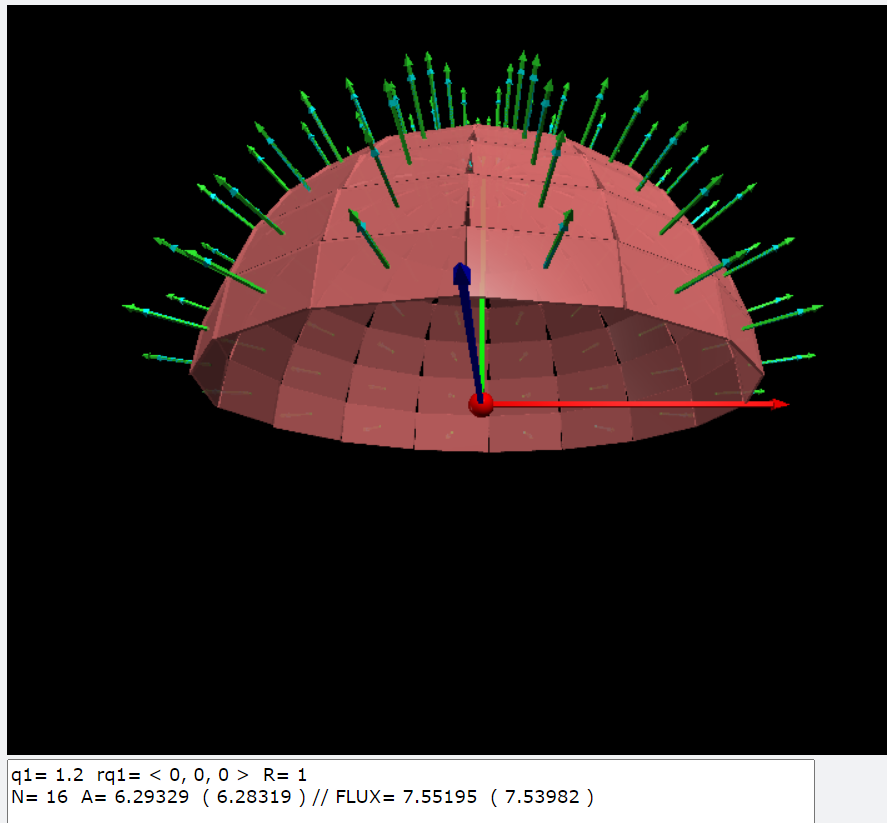
GlowScript 3.2 VPython
scene=canvas(width=800, height=600, center=vector(0.1,0.1,0), forward=vec(0,0.3,-1))
X=arrow(pos=vec(0,0,0),axis=vec(1.2,0,0),shaftwidth=0.02,headwidth=0.04,color=vec(1,0,0))
Y=arrow(pos=vec(0,0,0),axis=vec(0,1.2,0),shaftwidth=0.02,headwidth=0.04,color=vec(0,1,0))
Z=arrow(pos=vec(0,0,0),axis=vec(0,0,1.2),shaftwidth=0.02,headwidth=0.04,color=vec(0,0,1))
R=1; N=16; dt=pi/N; df=2*pi/N
q1=1.2; rq1=vec(0.,0.0,0.); ke=1
Q1=sphere(pos=rq1,radius=0.05,color=vec(1,0,0))
A=0; FLUX=0
for i in range(N/2):
    t=dt*(i+0.5)
    for j in range(N):
        f=df*(j+0.5)
        x=R*sin(t)*cos(f); z=R*sin(t)*sin(f); y=R*cos(t)
        r=vec(x,y,z)
        n=hat(r)
        r1=vec(R*sin(t+0.01)*cos(f),R*cos(t+0.01),R*sin(t+0.01)*sin(f))
        tv=hat(r1-r)
        b=box(pos=r,size=vec(R*dt,0.01,R*sin(t)*df),axis=tv,up=r,color=vec(1,0.5,0.5),opacity=0.7)
        E=ke*q1/mag2(r-rq1)*hat(r-rq1)
        #arrow(pos=r,axis=b.axis,shaftwidth=0.01,headwidth=0.02,color=vec(1,1,0))
        arrow(pos=r,axis=b.up*0.2,shaftwidth=0.01,headwidth=0.02,color=vec(0,1,1))
        arrow(pos=r,axis=E*0.2,shaftwidth=0.01,headwidth=0.02,color=vec(0.2,1,0.2))
        A+=R**2*sin(t)*dt*df
        FLUX+=dot(E,n)*R**2*sin(t)*dt*df
print('q1=',q1,' rq1=',rq1,' R=',R)
print('N=',N,' A=',A,' (',2*pi*R**2,') // FLUX=',FLUX,' (',2*pi*q1,')')

q1= 1.2  rq1= < 0, 0, 0 >  R= 1
N= 8  A= 6.32374  ( 6.28319 ) // FLUX= 7.58849  ( 7.53982 )
N= 16  A= 6.29329  ( 6.28319 ) // FLUX= 7.55195  ( 7.53982 )
N= 32  A= 6.28571  ( 6.28319 ) // FLUX= 7.54285  ( 7.53982 )
N= 64  A= 6.28382  ( 6.28319 ) // FLUX= 7.54058  ( 7.53982 )
N= 128  A= 6.28334  ( 6.28319 ) // FLUX= 7.54001  ( 7.53982 )

glowscript:一個點電荷對半球面的電通量(PS-EFlux-09.py)